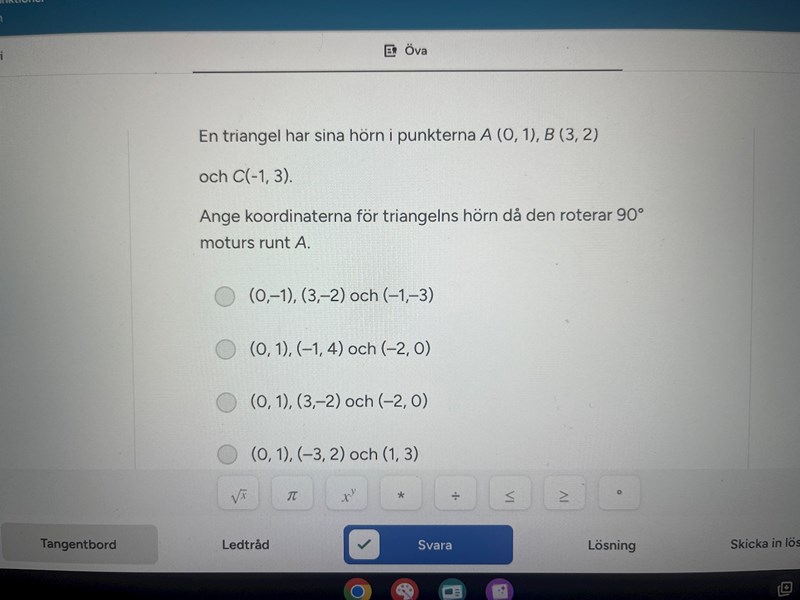
90 graders Koordinater
Hej, hur kan man lösa den här frågan utan att använda vektorer då jag inte lärt mig det än?
Man kan ta ett (rutat) papper och rita. Det är ofta bra.
jag ritade startpunkten lägst upp sedan b c och d men inte a då jag visste från allra början att det inte kunde vara den, men här gissade jag bara fram att alternativ b var korrekt men vet inte hur jag kan förklara det.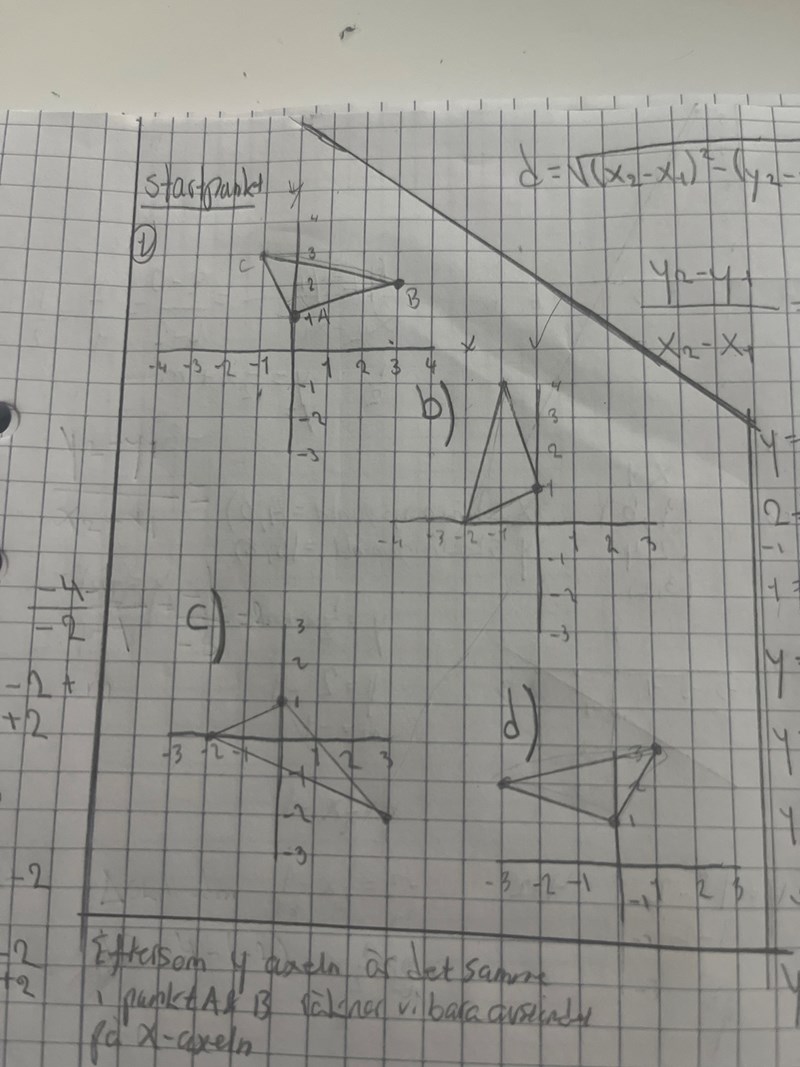
Du har rätt i att (b) är rätt. Alla sidor i triangeln är lika långa, men nu vinkelräta (-90 grader) mot hur de var tidigare. I din figur (b) har du ju samma punkter som svaralternativet.
Visa spoiler

sictransit skrev:Du har rätt i att (b) är rätt. Alla sidor i triangeln är lika långa, men nu vinkelräta (-90 grader) mot hur de var tidigare. I din figur (b) har du ju samma punkter som svaralternativet.
jag har enbart utgått från frågan som angav dessa koordinater till startpunkten, skulle jag ha gjort på ett annat sätt?
Nej, du har ju kommit fram till rätt svar genom att rotera figuren grafiskt. Det finns andra metoder också förstås, men kanske inte i Matte 1.
Trinity2 skrev:Visa spoiler
Hur visste du att den skulle hamna på 4 för y axeln?
sictransit skrev:Nej, du har ju kommit fram till rätt svar genom att rotera figuren grafiskt. Det finns andra metoder också förstås, men kanske inte i Matte 1.
Finns det någon metod som man kan använda som inte kräver mycket tid för sådana frågor?
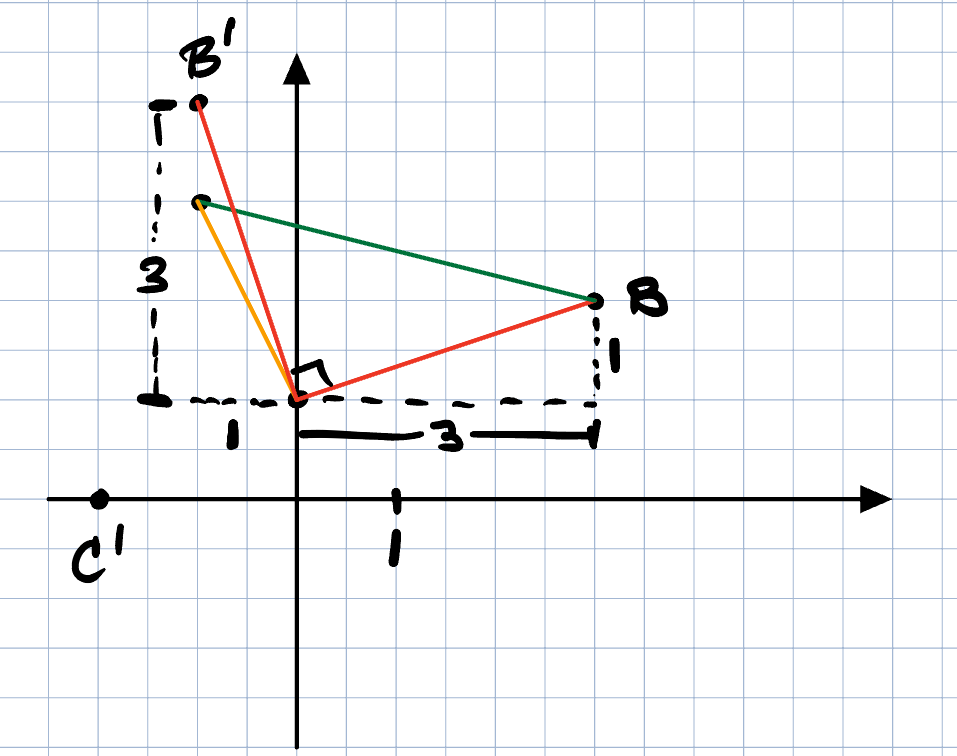
Ja, du kan flytta figuren så att A hamnar i origo genom att subtrahera A (0,1) från samtliga punkter. A blir då (0,0).
Sedan använder du följande för rotation moturs 90 grader: (x,y) -> (-y,x).
Nu har du tre nya punkter med A fortfarande i origo.
Eftersom du subtraherat (0,1) tidigare måste du nu addera (0,1) igen till samtliga punkter.
Detta fungerar, men jag vet inte hur det är tänkt att du skall göra på din nivå just nu.
Jag skulle använda en annan metod, snarlik, linjär algebra och definitivt inte Matte 1.
Abarnet skrev:Trinity2 skrev:Visa spoiler
Hur visste du att den skulle hamna på 4 för y axeln?
Du kan tingen se det som kvadrater då rotationen är 90 grader
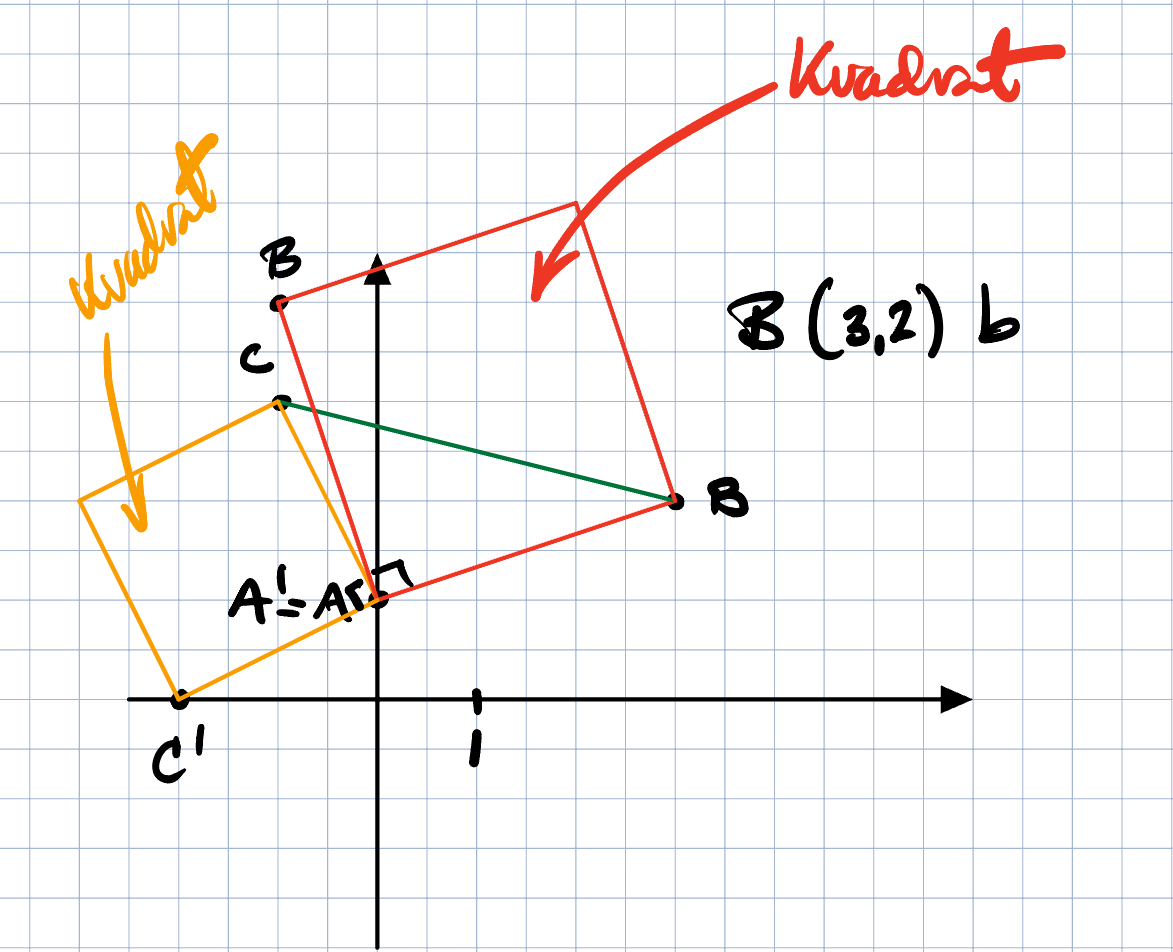
eller se vilken stigning en sida har