"a försummas i VL eftersom det är litet"
Hej.
Min fråga är om man verkligen kan göra så?

mvh
maratmatorkin skrev:Hej.
Min fråga är om man verkligen kan göra så?
mvh
Nja, det är väl en lite "förenklad" version. Man skall tänka på att när Barrow verkade så hade varken Newton eller Leibniz gjort sina stora upptäckter. Det var inte alltid det var stringenta bevis, men de hade oftast exceptionell intuition. Om du hoppar över "tag bort a" kommer du att få
PQ=2x+ay
och här får man då tillämpa gränsvärde (vilket kanske inte Barrow var förtrogen med på sin tid) och får, då a->0 och y är begränsad, vilket y=rot(x) är, d.v.s. den skenar inte med ett minskande a
PQ -> 2x då a->0 (vilket innebär att e->0)
Så i gränsövergången, där just tangenten existerar, får vi den önskade egenskapen visad i bilden.
Newton skrattade nog gott åt detta senare och skrev diff.ekv.
y'=y/(2x)
vilken har lösningen y=C rot(x) vilket visar på samma sak, fast enklare. Notera att det gäller för alla C=/=0.
Att lösa denna typ av diff.ekv. är dock Ma4 (tror jag, eller Ma5?), men du kan alltid derivera och verifiera att det är en lösning till diff.ekv.
Trinity2 skrev:maratmatorkin skrev:Hej.
Min fråga är om man verkligen kan göra så?
mvh
Nja, det är väl en lite "förenklad" version. Man skall tänka på att när Barrow verkade så hade varken Newton eller Leibniz gjort sina stora upptäckter. Det var inte alltid det var stringenta bevis, men de hade oftast exceptionell intuition. Om du hoppar över "tag bort a" kommer du att få
PQ=2x+ay
och här får man då tillämpa gränsvärde (vilket kanske inte Barrow var förtrogen med på sin tid) och får, då a->0 och y är begränsad, vilket y=rot(x) är, d.v.s. den skenar inte med ett minskande a
Vad menas med begränsad och att den inte skenar? Menar du att funktionen är kontinuerlig och definierad för alla x vilket inte är fallet då nämnaren i en polynomfunktion är 0?
PQ -> 2x då a->0 (vilket innebär att e->0)
Så i gränsövergången, där just tangenten existerar, får vi den önskade egenskapen visad i bilden.
Newton skrattade nog gott åt detta senare och skrev diff.ekv.
y'=y/(2x)
vilken har lösningen y=C rot(x) vilket visar på samma sak, fast enklare. Notera att det gäller för alla C=/=0.
Att lösa denna typ av diff.ekv. är dock Ma4 (tror jag, eller Ma5?), men du kan alltid derivera och verifiera att det är en lösning till diff.ekv.
okej tack. Sista stycket var lite oklart men det är bättre att läsa om detta i boken i nästa kurs.
maratmatorkin skrev:Trinity2 skrev:maratmatorkin skrev:Hej.
Min fråga är om man verkligen kan göra så?
mvh
Nja, det är väl en lite "förenklad" version. Man skall tänka på att när Barrow verkade så hade varken Newton eller Leibniz gjort sina stora upptäckter. Det var inte alltid det var stringenta bevis, men de hade oftast exceptionell intuition. Om du hoppar över "tag bort a" kommer du att få
PQ=2x+ay
och här får man då tillämpa gränsvärde (vilket kanske inte Barrow var förtrogen med på sin tid) och får, då a->0 och y är begränsad, vilket y=rot(x) är, d.v.s. den skenar inte med ett minskande a
Vad menas med begränsad och att den inte skenar? Menar du att funktionen är kontinuerlig och definierad för alla x vilket inte är fallet då nämnaren i en polynomfunktion är 0?
PQ -> 2x då a->0 (vilket innebär att e->0)
Så i gränsövergången, där just tangenten existerar, får vi den önskade egenskapen visad i bilden.
Newton skrattade nog gott åt detta senare och skrev diff.ekv.
y'=y/(2x)
vilken har lösningen y=C rot(x) vilket visar på samma sak, fast enklare. Notera att det gäller för alla C=/=0.
Att lösa denna typ av diff.ekv. är dock Ma4 (tror jag, eller Ma5?), men du kan alltid derivera och verifiera att det är en lösning till diff.ekv.
okej tack. Sista stycket var lite oklart men det är bättre att läsa om detta i boken i nästa kurs.
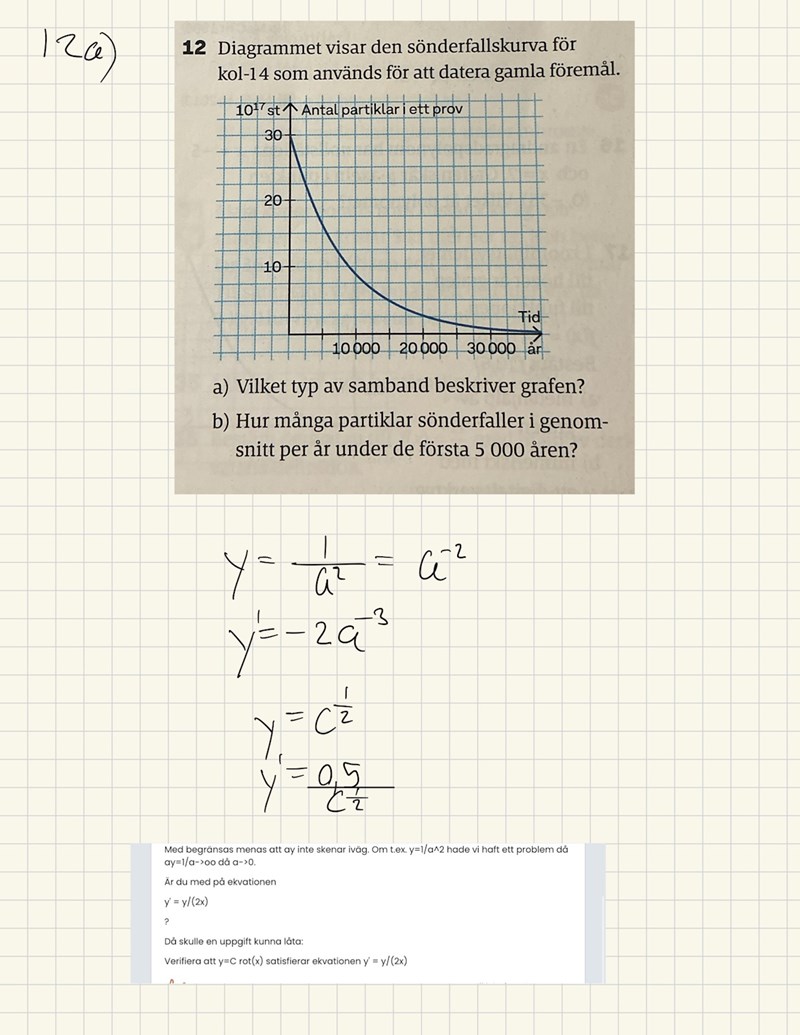
Med begränsas menas att ay inte skenar iväg. Om t.ex. y=1/a^2 hade vi haft ett problem då ay=1/a->oo då a->0.
Är du med på ekvationen
y' = y/(2x)
?
Då skulle en uppgift kunna låta:
Verifiera att y=C rot(x) satisfierar ekvationen y' = y/(2x)
Trinity2 skrev:maratmatorkin skrev:Trinity2 skrev:maratmatorkin skrev:Hej.
Min fråga är om man verkligen kan göra så?
mvh
Nja, det är väl en lite "förenklad" version. Man skall tänka på att när Barrow verkade så hade varken Newton eller Leibniz gjort sina stora upptäckter. Det var inte alltid det var stringenta bevis, men de hade oftast exceptionell intuition. Om du hoppar över "tag bort a" kommer du att få
PQ=2x+ay
och här får man då tillämpa gränsvärde (vilket kanske inte Barrow var förtrogen med på sin tid) och får, då a->0 och y är begränsad, vilket y=rot(x) är, d.v.s. den skenar inte med ett minskande a
Vad menas med begränsad och att den inte skenar? Menar du att funktionen är kontinuerlig och definierad för alla x vilket inte är fallet då nämnaren i en polynomfunktion är 0?
PQ -> 2x då a->0 (vilket innebär att e->0)
Så i gränsövergången, där just tangenten existerar, får vi den önskade egenskapen visad i bilden.
Newton skrattade nog gott åt detta senare och skrev diff.ekv.
y'=y/(2x)
vilken har lösningen y=C rot(x) vilket visar på samma sak, fast enklare. Notera att det gäller för alla C=/=0.
Att lösa denna typ av diff.ekv. är dock Ma4 (tror jag, eller Ma5?), men du kan alltid derivera och verifiera att det är en lösning till diff.ekv.
okej tack. Sista stycket var lite oklart men det är bättre att läsa om detta i boken i nästa kurs.
Med begränsas menas att ay inte skenar iväg. Om t.ex. y=1/a^2 hade vi haft ett problem då ay=1/a->oo då a->0.
Är du med på ekvationen
y' = y/(2x)
?
Då skulle en uppgift kunna låta:
Verifiera att y=C rot(x) satisfierar ekvationen y' = y/(2x)
Jo men det tror jag att jag är med på när a går mot 0.
Sen tappar du mig. Inte gått igenom deriveringsreglerna mer än att jag satt med under en lektion i några timmar. Uppfattar jag y=C rot(x) rätt? Eller det gör jag nog inte ser jag nu. Kan du visa?
maratmatorkin skrev:Trinity2 skrev:maratmatorkin skrev:Trinity2 skrev:maratmatorkin skrev:Hej.
Min fråga är om man verkligen kan göra så?
mvh
Nja, det är väl en lite "förenklad" version. Man skall tänka på att när Barrow verkade så hade varken Newton eller Leibniz gjort sina stora upptäckter. Det var inte alltid det var stringenta bevis, men de hade oftast exceptionell intuition. Om du hoppar över "tag bort a" kommer du att få
PQ=2x+ay
och här får man då tillämpa gränsvärde (vilket kanske inte Barrow var förtrogen med på sin tid) och får, då a->0 och y är begränsad, vilket y=rot(x) är, d.v.s. den skenar inte med ett minskande a
Vad menas med begränsad och att den inte skenar? Menar du att funktionen är kontinuerlig och definierad för alla x vilket inte är fallet då nämnaren i en polynomfunktion är 0?
PQ -> 2x då a->0 (vilket innebär att e->0)
Så i gränsövergången, där just tangenten existerar, får vi den önskade egenskapen visad i bilden.
Newton skrattade nog gott åt detta senare och skrev diff.ekv.
y'=y/(2x)
vilken har lösningen y=C rot(x) vilket visar på samma sak, fast enklare. Notera att det gäller för alla C=/=0.
Att lösa denna typ av diff.ekv. är dock Ma4 (tror jag, eller Ma5?), men du kan alltid derivera och verifiera att det är en lösning till diff.ekv.
okej tack. Sista stycket var lite oklart men det är bättre att läsa om detta i boken i nästa kurs.
Med begränsas menas att ay inte skenar iväg. Om t.ex. y=1/a^2 hade vi haft ett problem då ay=1/a->oo då a->0.
Är du med på ekvationen
y' = y/(2x)
?
Då skulle en uppgift kunna låta:
Verifiera att y=C rot(x) satisfierar ekvationen y' = y/(2x)
Jo men det tror jag att jag är med på när a går mot 0.
Sen tappar du mig. Inte gått igenom deriveringsreglerna mer än att jag satt med under en lektion i några timmar. Uppfattar jag y=C rot(x) rätt? Eller det gör jag nog inte ser jag nu. Kan du visa?
Så här
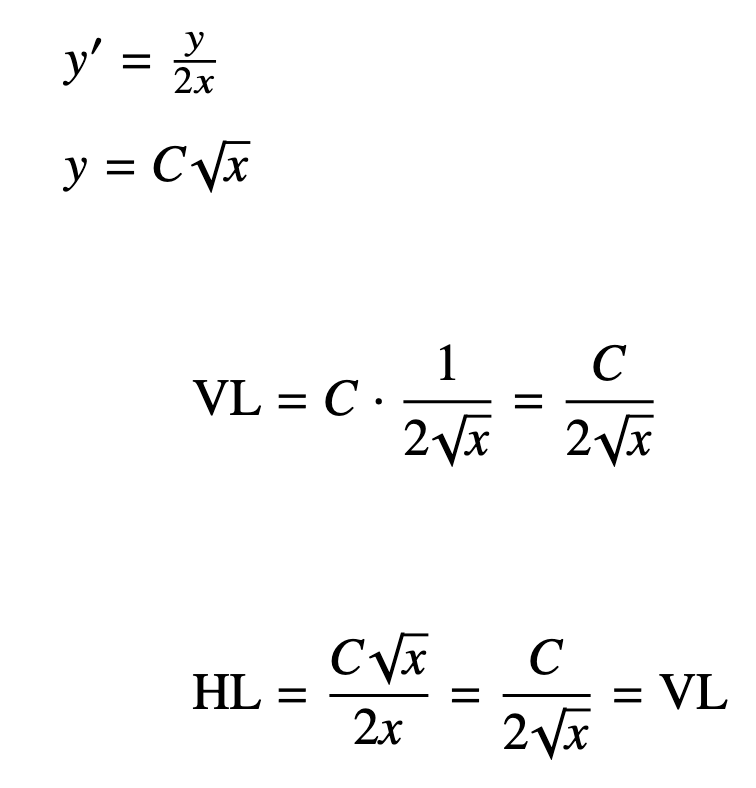
Jag får backa bandet lite och se på det med nya ögon efter en god natts sömn.


