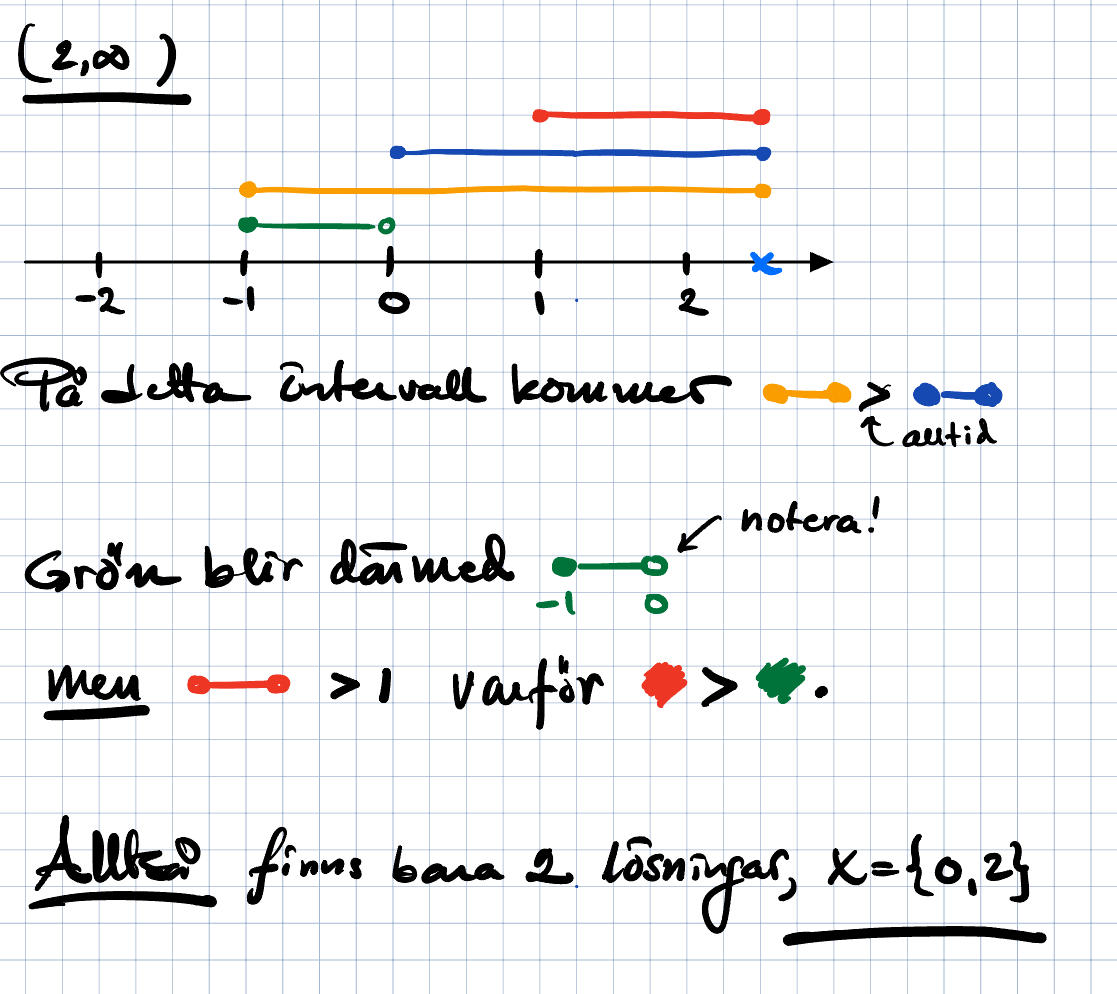
Absolutbellop

Vill man vara petig vill man göra intervall som följer absolutbeloppets definition

$\left|x\right|=\left\{\begin{array}{ll}x& , x\ge 0\\ -x& , x<0\end{array}\right.$, alltså att i varje brytpunkt är det $x$ större eller lika med och inte bara större än. Skillnaden är då att dina intervall blir

$x<-1$

$-1\leq x < 1$

och

$1 \leq x$. 

Är det korrekt att din ekvation är

$\left|\left|x+1\right|-\left|x\right|\right|=\left|1-x\right|$

?

MrPotatohead skrev:

Vill man vara petig vill man göra intervall som följer absolutbeloppets definition

$\left|x\right|=\left\{\begin{array}{ll}x& , x\ge 0\\ -x& , x<0\end{array}\right.$, alltså att i varje brytpunkt är det $x$ större eller lika med och inte bara större än. Skillnaden är då att dina intervall blir

$x<-1$

$-1\leq x < 1$

och

$1 \leq x$. 

Är det korrekt att din ekvation är

$\left|\left|x+1\right|-\left|x\right|\right|=\left|1-x\right|$

?

ja, det är ett absolutbellopp inom absolutbellopp

ABC1 skrev:

Okej kolla, denna uppgift har inte ens en ända lärare kunnat förklara på ett bra sätt på hur man gör och upprepar samma tekniker vid liknande uppgiter. kan någon typ skriva en step-by-step på hur man igentligen ska tänka kring aboslutbellop och just denna uppgift.

Uppgift:
​∣ ∣x+1∣−∣x∣​ ∣=∣1−x∣

Vad jag tror jag vet:

Jag vet att man ska tänka innifrån och arbete sig utåt (tror)

När jag fått alla intervall för x, För de de inre absolutbellopen + den på HL 

 

• x<−1

• x≥−1

• x≥0

• x<0

• x≤1

• x>1

Ett problem jag har här är att sammansätta dessa till fall som täcker alla tillåtna värden. Jag har svårt med detta i enklare uppgifter men på något sätt fungerar det för mig genom att enbart tänka logiskt, Här funkar tyvätt inte samma tankesätt och jag skulle uppskatta en bättre förklaring på hur man tänker kring intervallen och hur man enklare ser vilka och hur många fall det blir. jag försökte rita upp en talllinje och skriva ut alla tillåtna värden för x för att se när och vart de överlappar. Men jag vet inte vad det är jag ska leta efter och hur jag ska tolka det.

Min gissning är detta:

• x<−1

• −1≤x≤1

• x>1

  Längre än detta kommer jag inte och behöver hjälp att förstå hur man tolkar de olika intervallen och hur man försöker sätta upp möjliga fall

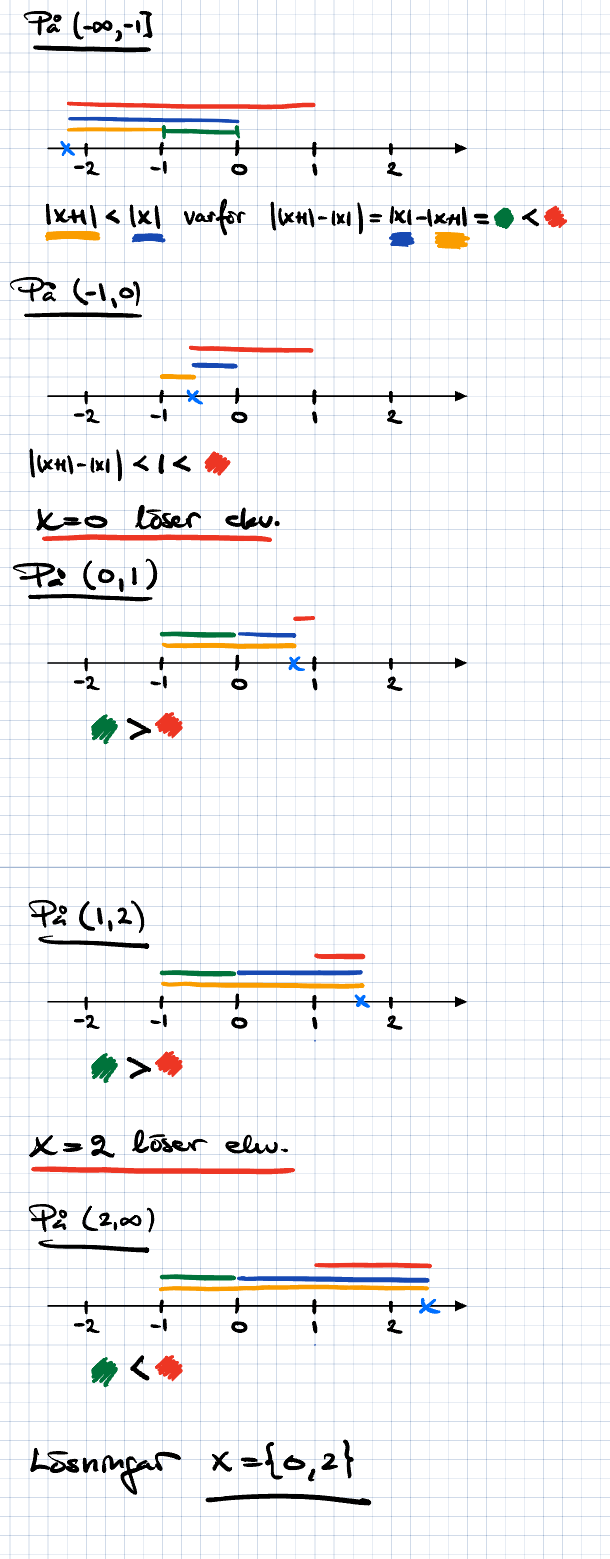
Jag hade provat enl nedan. Men, ja, man får hålla tungan rätt i mun …

Trinity2 skrev:

ABC1 skrev:

Okej kolla, denna uppgift har inte ens en ända lärare kunnat förklara på ett bra sätt på hur man gör och upprepar samma tekniker vid liknande uppgiter. kan någon typ skriva en step-by-step på hur man igentligen ska tänka kring aboslutbellop och just denna uppgift.

Uppgift:
​∣ ∣x+1∣−∣x∣​ ∣=∣1−x∣

Vad jag tror jag vet:

Jag vet att man ska tänka innifrån och arbete sig utåt (tror)

När jag fått alla intervall för x, För de de inre absolutbellopen + den på HL 

 

• x<−1

• x≥−1

• x≥0

• x<0

• x≤1

• x>1

Ett problem jag har här är att sammansätta dessa till fall som täcker alla tillåtna värden. Jag har svårt med detta i enklare uppgifter men på något sätt fungerar det för mig genom att enbart tänka logiskt, Här funkar tyvätt inte samma tankesätt och jag skulle uppskatta en bättre förklaring på hur man tänker kring intervallen och hur man enklare ser vilka och hur många fall det blir. jag försökte rita upp en talllinje och skriva ut alla tillåtna värden för x för att se när och vart de överlappar. Men jag vet inte vad det är jag ska leta efter och hur jag ska tolka det.

Min gissning är detta:

• x<−1

• −1≤x≤1

• x>1

  Längre än detta kommer jag inte och behöver hjälp att förstå hur man tolkar de olika intervallen och hur man försöker sätta upp möjliga fall

Jag hade provat enl nedan. Men, ja, man får hålla tungan rätt i mun …

jag kasnske är lite jobbig nu, men skulle du bara kortfattat kunna gå igenom hur ock varför du tagit dessa steg så jag får det lite lättare för mig att tolka vad exakt du har gjort och varför du tagit dessa steg för att komma fram till lösningarna. och vart den yttre aboslutbellopet spelar sin roll i svaret?

tack i förväg

ABC1 skrev:

Trinity2 skrev:

Visa föregående citat

ABC1 skrev:

Okej kolla, denna uppgift har inte ens en ända lärare kunnat förklara på ett bra sätt på hur man gör och upprepar samma tekniker vid liknande uppgiter. kan någon typ skriva en step-by-step på hur man igentligen ska tänka kring aboslutbellop och just denna uppgift.

Uppgift:
​∣ ∣x+1∣−∣x∣​ ∣=∣1−x∣

Vad jag tror jag vet:

Jag vet att man ska tänka innifrån och arbete sig utåt (tror)

När jag fått alla intervall för x, För de de inre absolutbellopen + den på HL 

 

• x<−1

• x≥−1

• x≥0

• x<0

• x≤1

• x>1

Ett problem jag har här är att sammansätta dessa till fall som täcker alla tillåtna värden. Jag har svårt med detta i enklare uppgifter men på något sätt fungerar det för mig genom att enbart tänka logiskt, Här funkar tyvätt inte samma tankesätt och jag skulle uppskatta en bättre förklaring på hur man tänker kring intervallen och hur man enklare ser vilka och hur många fall det blir. jag försökte rita upp en talllinje och skriva ut alla tillåtna värden för x för att se när och vart de överlappar. Men jag vet inte vad det är jag ska leta efter och hur jag ska tolka det.

Min gissning är detta:

• x<−1

• −1≤x≤1

• x>1

  Längre än detta kommer jag inte och behöver hjälp att förstå hur man tolkar de olika intervallen och hur man försöker sätta upp möjliga fall

Jag hade provat enl nedan. Men, ja, man får hålla tungan rätt i mun …

jag kasnske är lite jobbig nu, men skulle du bara kortfattat kunna gå igenom hur ock varför du tagit dessa steg så jag får det lite lättare för mig att tolka vad exakt du har gjort och varför du tagit dessa steg för att komma fram till lösningarna. och vart den yttre aboslutbellopet spelar sin roll i svaret?

tack i förväg

OK! Skall bara svälja en pizza och Coca-Cola med is. Återkommer med lite mera utförlig text.

Trinity2 skrev:

ABC1 skrev:

Visa föregående citat

Trinity2 skrev:

ABC1 skrev:

Okej kolla, denna uppgift har inte ens en ända lärare kunnat förklara på ett bra sätt på hur man gör och upprepar samma tekniker vid liknande uppgiter. kan någon typ skriva en step-by-step på hur man igentligen ska tänka kring aboslutbellop och just denna uppgift.

Uppgift:
​∣ ∣x+1∣−∣x∣​ ∣=∣1−x∣

Vad jag tror jag vet:

Jag vet att man ska tänka innifrån och arbete sig utåt (tror)

När jag fått alla intervall för x, För de de inre absolutbellopen + den på HL 

 

• x<−1

• x≥−1

• x≥0

• x<0

• x≤1

• x>1

Ett problem jag har här är att sammansätta dessa till fall som täcker alla tillåtna värden. Jag har svårt med detta i enklare uppgifter men på något sätt fungerar det för mig genom att enbart tänka logiskt, Här funkar tyvätt inte samma tankesätt och jag skulle uppskatta en bättre förklaring på hur man tänker kring intervallen och hur man enklare ser vilka och hur många fall det blir. jag försökte rita upp en talllinje och skriva ut alla tillåtna värden för x för att se när och vart de överlappar. Men jag vet inte vad det är jag ska leta efter och hur jag ska tolka det.

Min gissning är detta:

• x<−1

• −1≤x≤1

• x>1

  Längre än detta kommer jag inte och behöver hjälp att förstå hur man tolkar de olika intervallen och hur man försöker sätta upp möjliga fall

Jag hade provat enl nedan. Men, ja, man får hålla tungan rätt i mun …

jag kasnske är lite jobbig nu, men skulle du bara kortfattat kunna gå igenom hur ock varför du tagit dessa steg så jag får det lite lättare för mig att tolka vad exakt du har gjort och varför du tagit dessa steg för att komma fram till lösningarna. och vart den yttre aboslutbellopet spelar sin roll i svaret?

tack i förväg

OK! Skall bara svälja en pizza och Coca-Cola med is. Återkommer med lite mera utförlig text.

Hoppas det smakar! och sedan gärna en allmän förklaring för hur man kommer fram till fallen. Alltså hur jag ska gå från intervallen ex) x > 1 x<10 ... till sammansatta intervaller som täcker alla värden. Hitills har jag enbart gissat mig fram och kan igentligen inte se det läraren ser, när hon visar hur hon gör.

ABC1 skrev:

Trinity2 skrev:

Visa föregående citat

ABC1 skrev:

Trinity2 skrev:

Visa föregående citat

ABC1 skrev:

Okej kolla, denna uppgift har inte ens en ända lärare kunnat förklara på ett bra sätt på hur man gör och upprepar samma tekniker vid liknande uppgiter. kan någon typ skriva en step-by-step på hur man igentligen ska tänka kring aboslutbellop och just denna uppgift.

Uppgift:
​∣ ∣x+1∣−∣x∣​ ∣=∣1−x∣

Vad jag tror jag vet:

Jag vet att man ska tänka innifrån och arbete sig utåt (tror)

När jag fått alla intervall för x, För de de inre absolutbellopen + den på HL 

 

• x<−1

• x≥−1

• x≥0

• x<0

• x≤1

• x>1

Ett problem jag har här är att sammansätta dessa till fall som täcker alla tillåtna värden. Jag har svårt med detta i enklare uppgifter men på något sätt fungerar det för mig genom att enbart tänka logiskt, Här funkar tyvätt inte samma tankesätt och jag skulle uppskatta en bättre förklaring på hur man tänker kring intervallen och hur man enklare ser vilka och hur många fall det blir. jag försökte rita upp en talllinje och skriva ut alla tillåtna värden för x för att se när och vart de överlappar. Men jag vet inte vad det är jag ska leta efter och hur jag ska tolka det.

Min gissning är detta:

• x<−1

• −1≤x≤1

• x>1

  Längre än detta kommer jag inte och behöver hjälp att förstå hur man tolkar de olika intervallen och hur man försöker sätta upp möjliga fall

Jag hade provat enl nedan. Men, ja, man får hålla tungan rätt i

jag kasnske är lite jobbig nu, men skulle du bara kortfattat kunna gå igenom hur ock varför du tagit dessa steg så jag får det lite lättare för mig att tolka vad exakt du har gjort och varför du tagit dessa steg för att komma fram till lösningarna. och vart den yttre aboslutbellopet spelar sin roll i svaret?

tack i förväg

OK! Skall bara svälja en pizza och Coca-Cola med is. Återkommer med lite mera utförlig text.

Hoppas det smakar! och sedan gärna en allmän förklaring för hur man kommer fram till fallen. Alltså hur jag ska gå från intervallen ex) x > 1 x<10 ... till sammansatta intervaller som täcker alla värden. Hitills har jag enbart gissat mig fram och kan igentligen inte se det läraren ser, när hon visar hur hon gör.

Det satt fint, tack!

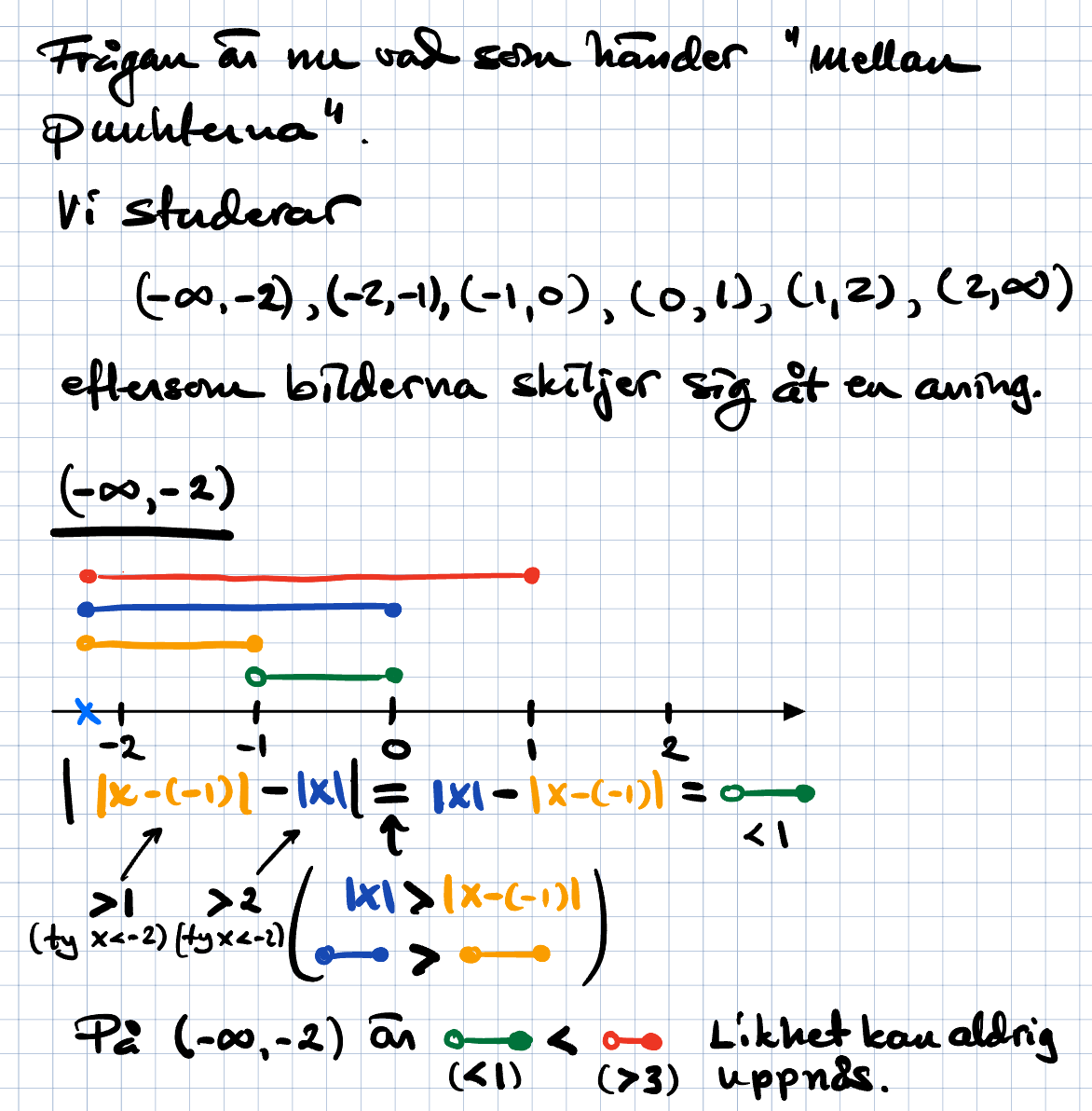
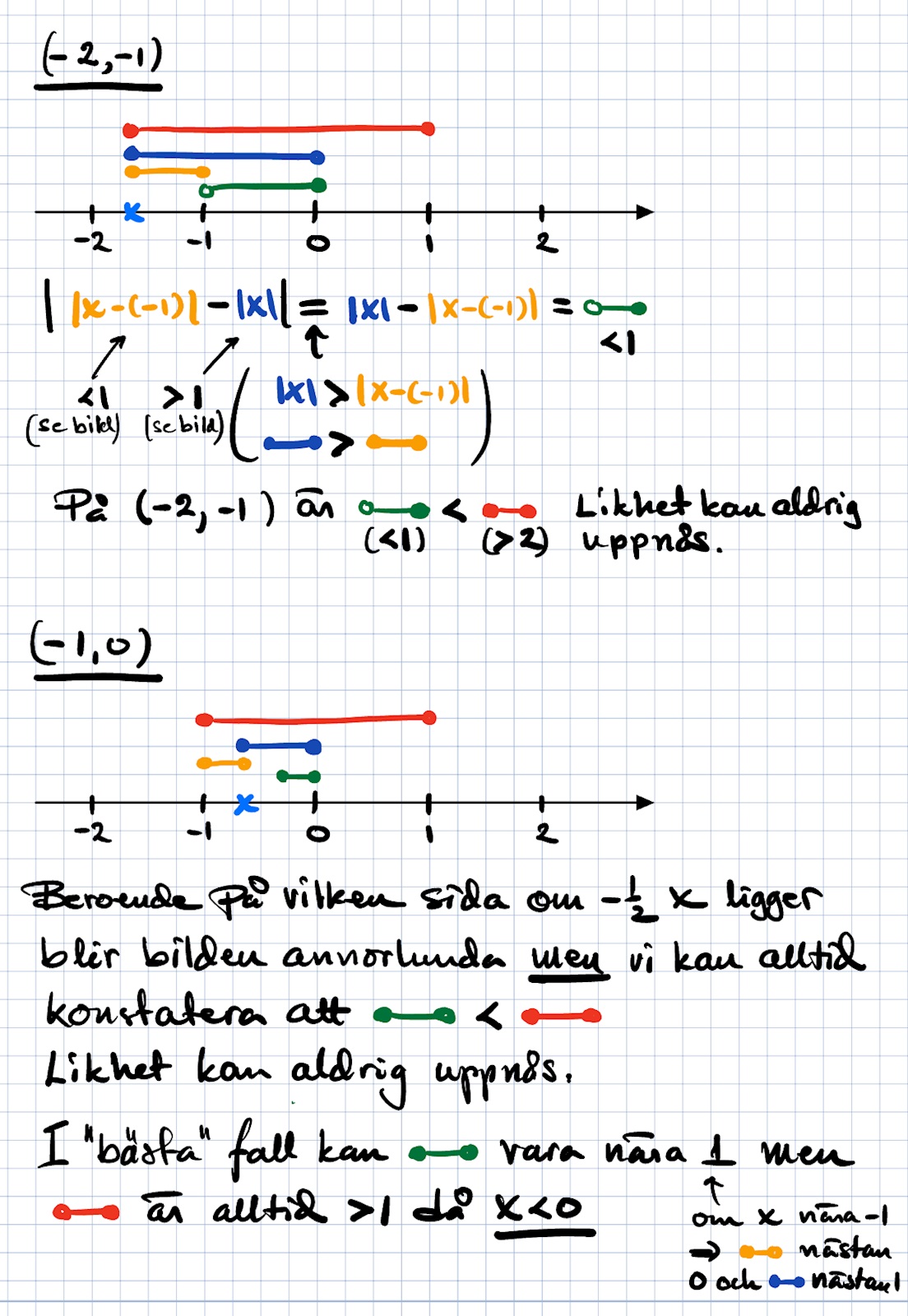
Vi får se om nedan kan ge lite substans…

Trinity2 skrev:

ABC1 skrev:

Visa föregående citat

Trinity2 skrev:

ABC1 skrev:

Visa föregående citat

Trinity2 skrev:

ABC1 skrev:

Okej kolla, denna uppgift har inte ens en ända lärare kunnat förklara på ett bra sätt på hur man gör och upprepar samma tekniker vid liknande uppgiter. kan någon typ skriva en step-by-step på hur man igentligen ska tänka kring aboslutbellop och just denna uppgift.

Uppgift:
​∣ ∣x+1∣−∣x∣​ ∣=∣1−x∣

Vad jag tror jag vet:

Jag vet att man ska tänka innifrån och arbete sig utåt (tror)

När jag fått alla intervall för x, För de de inre absolutbellopen + den på HL 

 

• x<−1

• x≥−1

• x≥0

• x<0

• x≤1

• x>1

Ett problem jag har här är att sammansätta dessa till fall som täcker alla tillåtna värden. Jag har svårt med detta i enklare uppgifter men på något sätt fungerar det för mig genom att enbart tänka logiskt, Här funkar tyvätt inte samma tankesätt och jag skulle uppskatta en bättre förklaring på hur man tänker kring intervallen och hur man enklare ser vilka och hur många fall det blir. jag försökte rita upp en talllinje och skriva ut alla tillåtna värden för x för att se när och vart de överlappar. Men jag vet inte vad det är jag ska leta efter och hur jag ska tolka det.

Min gissning är detta:

• x<−1

• −1≤x≤1

• x>1

  Längre än detta kommer jag inte och behöver hjälp att förstå hur man tolkar de olika intervallen och hur man försöker sätta upp möjliga fall

Jag hade provat enl nedan. Men, ja, man får hålla tungan rätt i

jag kasnske är lite jobbig nu, men skulle du bara kortfattat kunna gå igenom hur ock varför du tagit dessa steg så jag får det lite lättare för mig att tolka vad exakt du har gjort och varför du tagit dessa steg för att komma fram till lösningarna. och vart den yttre aboslutbellopet spelar sin roll i svaret?

tack i förväg

OK! Skall bara svälja en pizza och Coca-Cola med is. Återkommer med lite mera utförlig text.

Hoppas det smakar! och sedan gärna en allmän förklaring för hur man kommer fram till fallen. Alltså hur jag ska gå från intervallen ex) x > 1 x<10 ... till sammansatta intervaller som täcker alla värden. Hitills har jag enbart gissat mig fram och kan igentligen inte se det läraren ser, när hon visar hur hon gör.

Det satt fint, tack!

Vi får se om nedan kan ge lite substans…

Tack för svaret. har läst igenom ett par gånger och måste vara ärlig att jag inte fattar hela motiveringen. Kommer ha denna lösning i bakhuvet för att jag möjligen längre fram kunna förstå ditt sätt att lösa lite bättre. Men väldigt fint skrivet och förklarat annars. Måste också påpeka att ditt sätt att lösa uppgiften avviker från vad jag har sett lärare visa och detta gör det ännu bättre för någon som mig, då jag lär mig 10 gånger bättre när jag kan se flera vägar till en och samma lösning. Känns som ett extra verktyg i verktygslådan. Tack för din tid och ha en trevlig fredag kväll.

ABC1 skrev:

Trinity2 skrev:

Tack för svaret. har läst igenom ett par gånger och måste vara ärlig att jag inte fattar hela motiveringen. Kommer ha denna lösning i bakhuvet för att jag möjligen längre fram kunna förstå ditt sätt att lösa lite bättre. Men väldigt fint skrivet och förklarat annars. Måste också påpeka att ditt sätt att lösa uppgiften avviker från vad jag har sett lärare visa och detta gör det ännu bättre för någon som mig, då jag lär mig 10 gånger bättre när jag kan se flera vägar till en och samma lösning. Känns som ett extra verktyg i verktygslådan. Tack för din tid och ha en trevlig fredag kväll.

Ibland kan en rent algebraisk lösning vara fördelaktig, men att tänka på |...| som avstånd kan ha sin poäng, speciellt i komplexa tal längre fram, men även otrevliga absolututtryck som de verkar älska på Matematikprovet. Vet inte varför, de bara gör det…

dvsABC1 skrev:

 

Är det korrekt att din ekvation är

$\left|\left|x+1\right|-\left|x\right|\right|=\left|1-x\right|$

?

ja, det är ett absolutbellopp inom absolutbellopp

Skönt, men svårläst
Går inte att direkt se vilka  |  som hör ihop

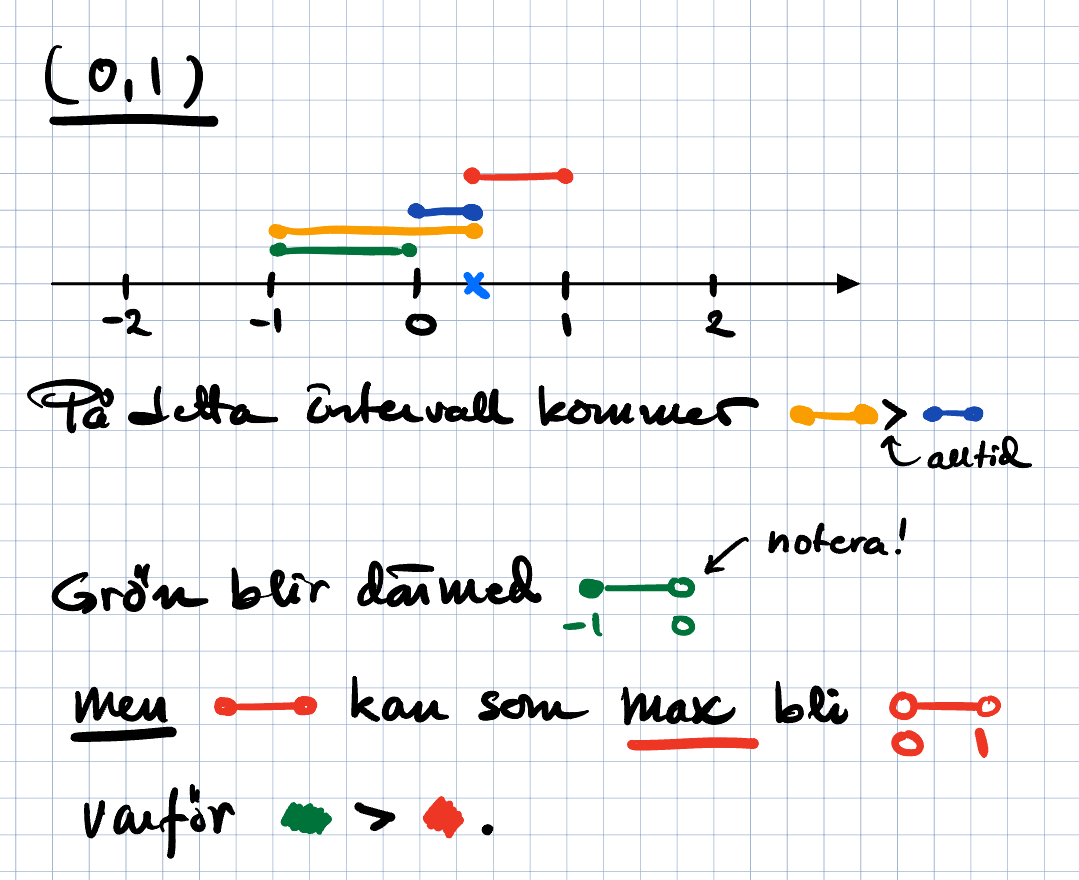
Förslag till grafisk lösning

Lite lättare blir det om man sätter parenteser runt uttrycket   |x+1| - |x|  .
Då blir VL:   | (|x+1| - |x|) |
Det kan vi hantera grafiskt

•  |x+1|  blir ett  V med spetsen nedåt i (-1, 0) 
   och "vingarna" uppåt med lutning  ±1  dvs  ±45°

•  –|x|  blir ett upp-och-nervänt  V med spetsen uppåt i (0, 0) 
    och "vingarna" nedåt med lutning  ±1  dvs  ±45°

Rita båda i samma koordinatsystem

Rita sedan "summagrafen" i samma koordinatsystem

Här har vi nu grafen till funktionen   |x+1| - |x|

Hur kommer då grafen till   | (|x+1| - |x|) |   att se ut?  Dvs grafen till VL

Rita grafen till VL i ett nytt koordinatsystem

Rita grafen till  HL , dvs till  |1-x| , i samma system och se var de skär varann.

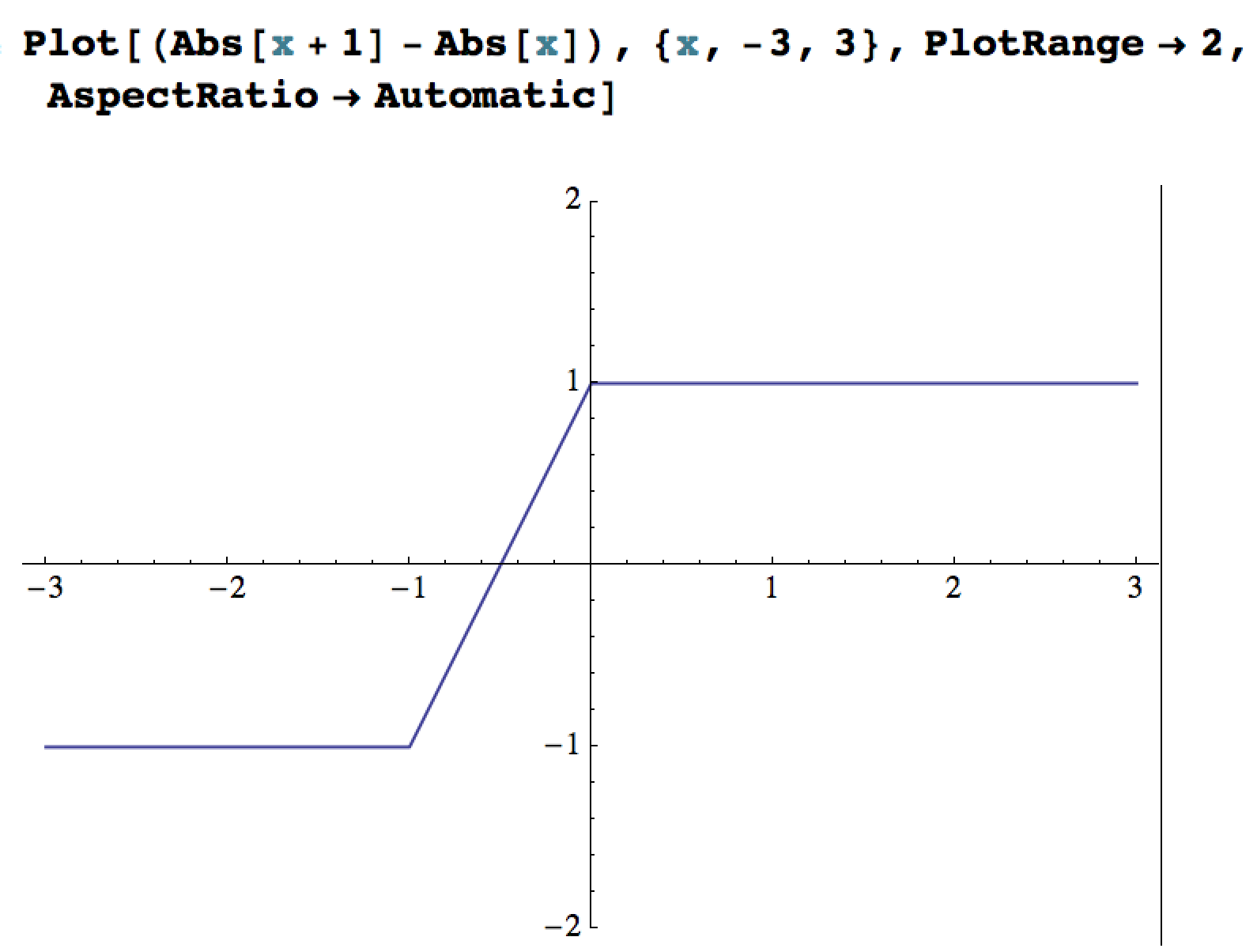
Ja, plotta är också en bra metod. 

1. Vi plottar alla tre grafer; Orange = |x+1|, Blå = |x|, Röd = |1-x|

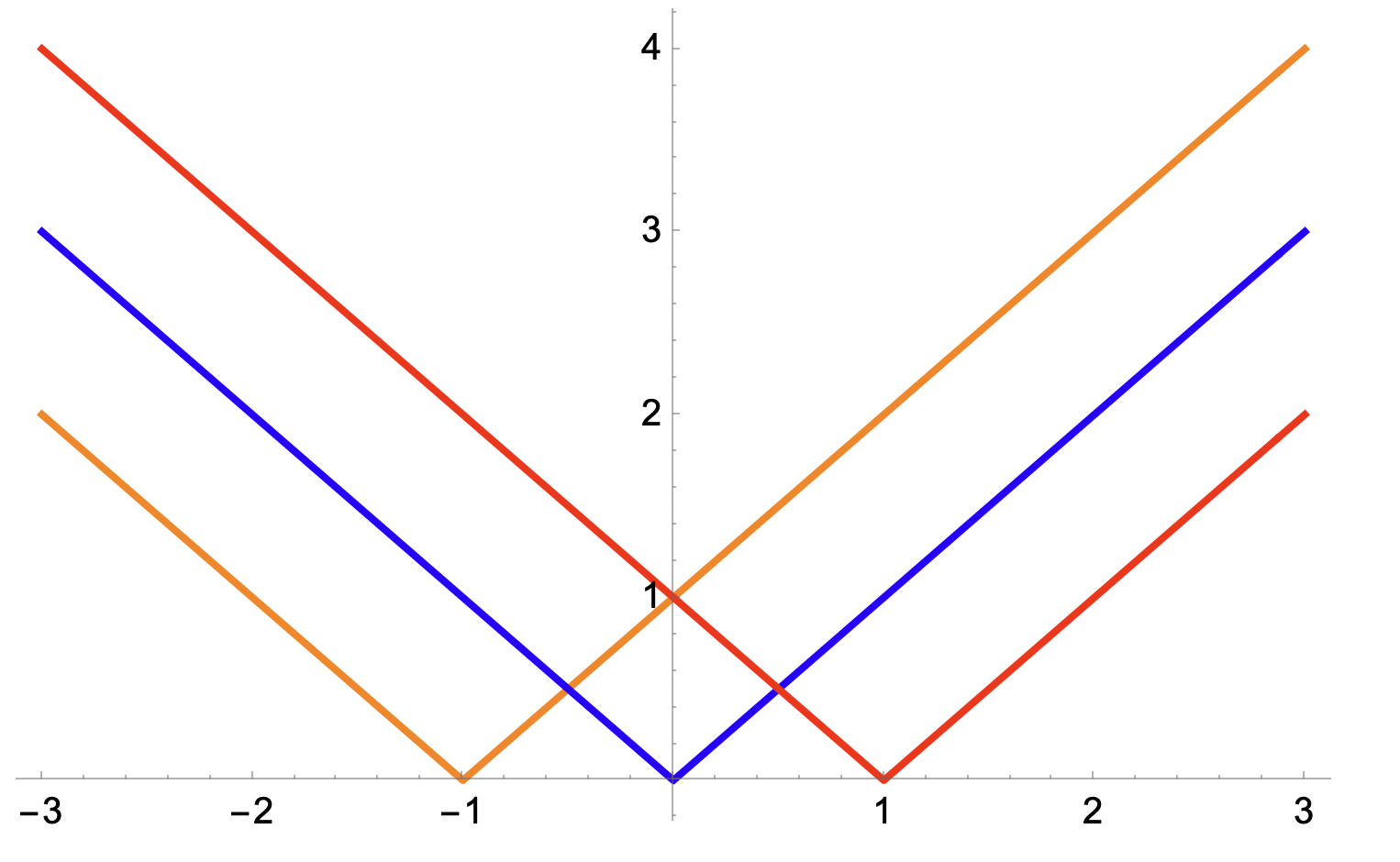
2. Differencen mellan orange och blå ger oss svart graf

3. Absolutbelopp på svart graf ger

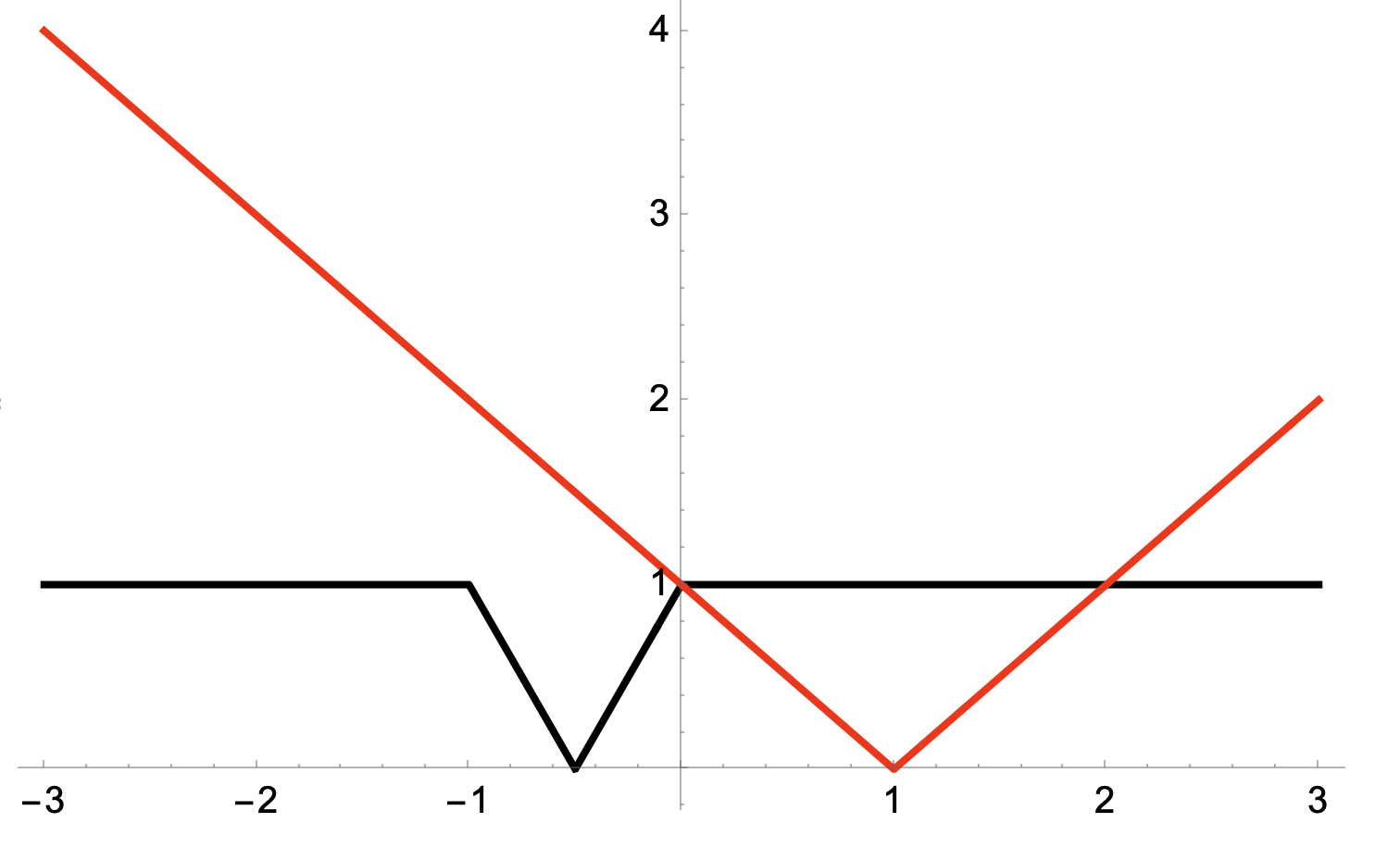
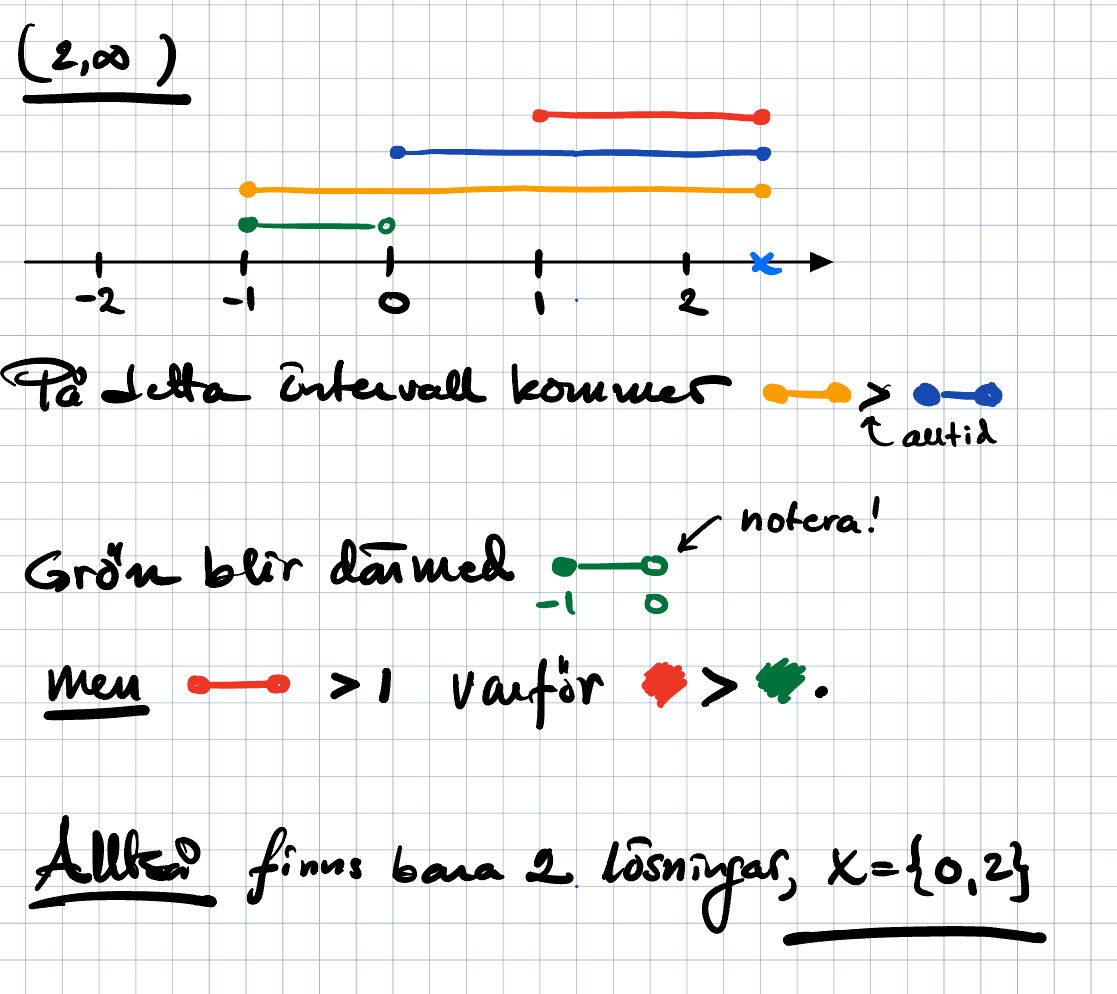
och där har vi våra 2 lösningar.

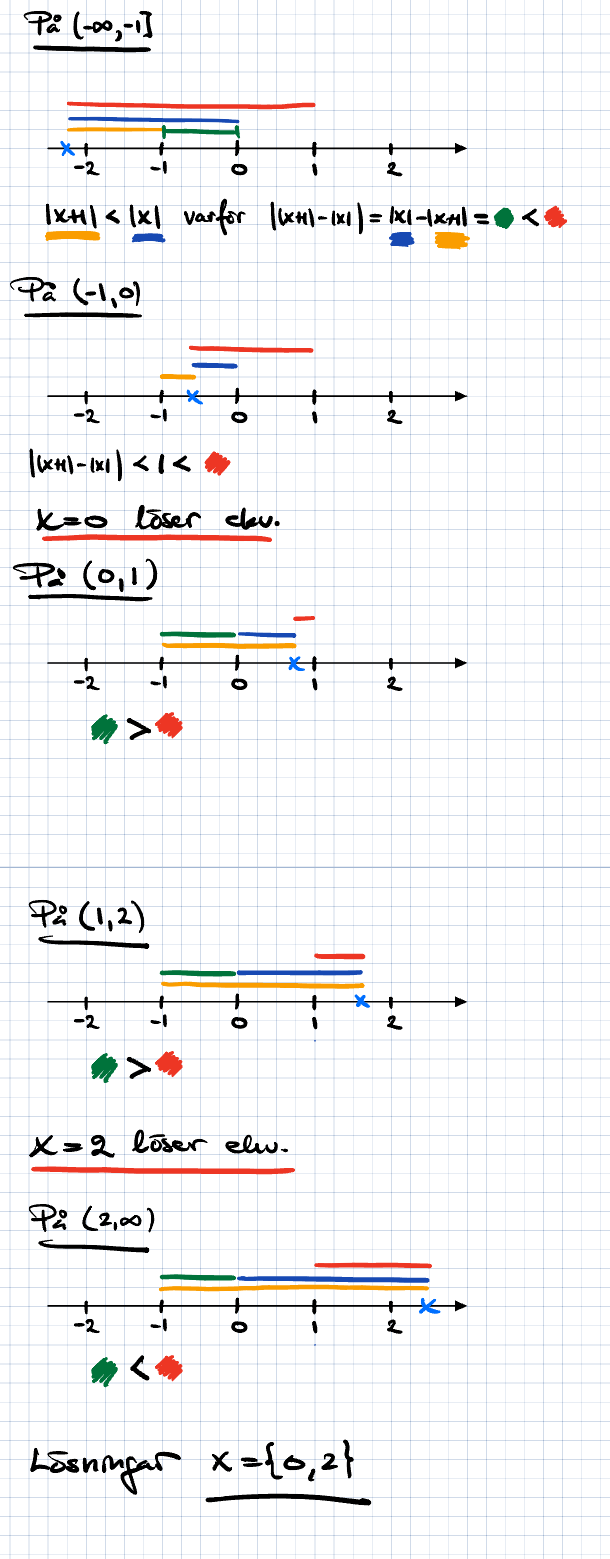
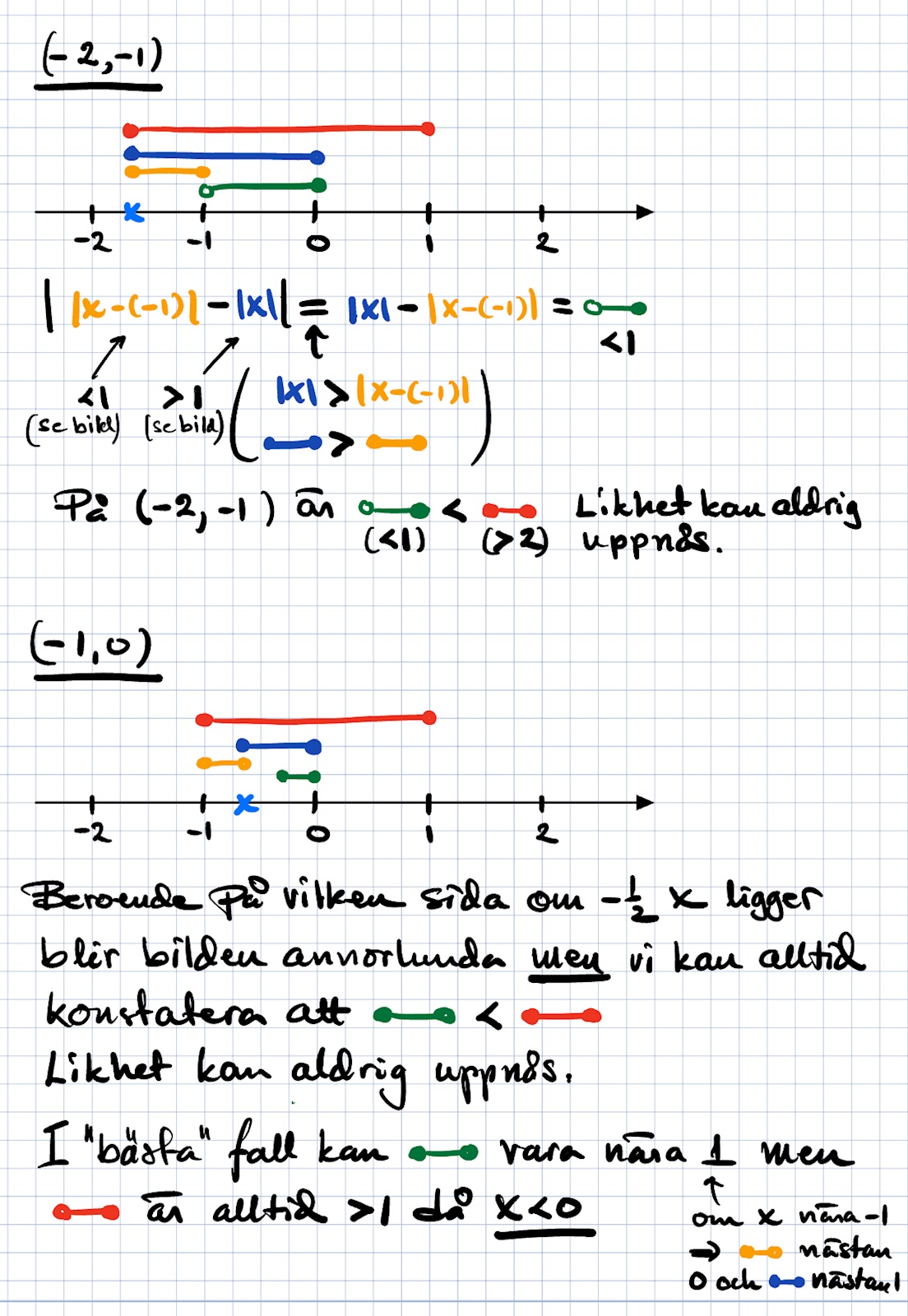
Om man vill ha en algebraisk metod som skulle gå att programmera en dator för, så tror jag det går bra om man arbetar inifrån och ut.

Först gäller det här |x+1| - |x|. Det uttrycket har brytpunkterna -1 och 1, och i de tre intervallen har det värdena

-1, 2x+1, 1

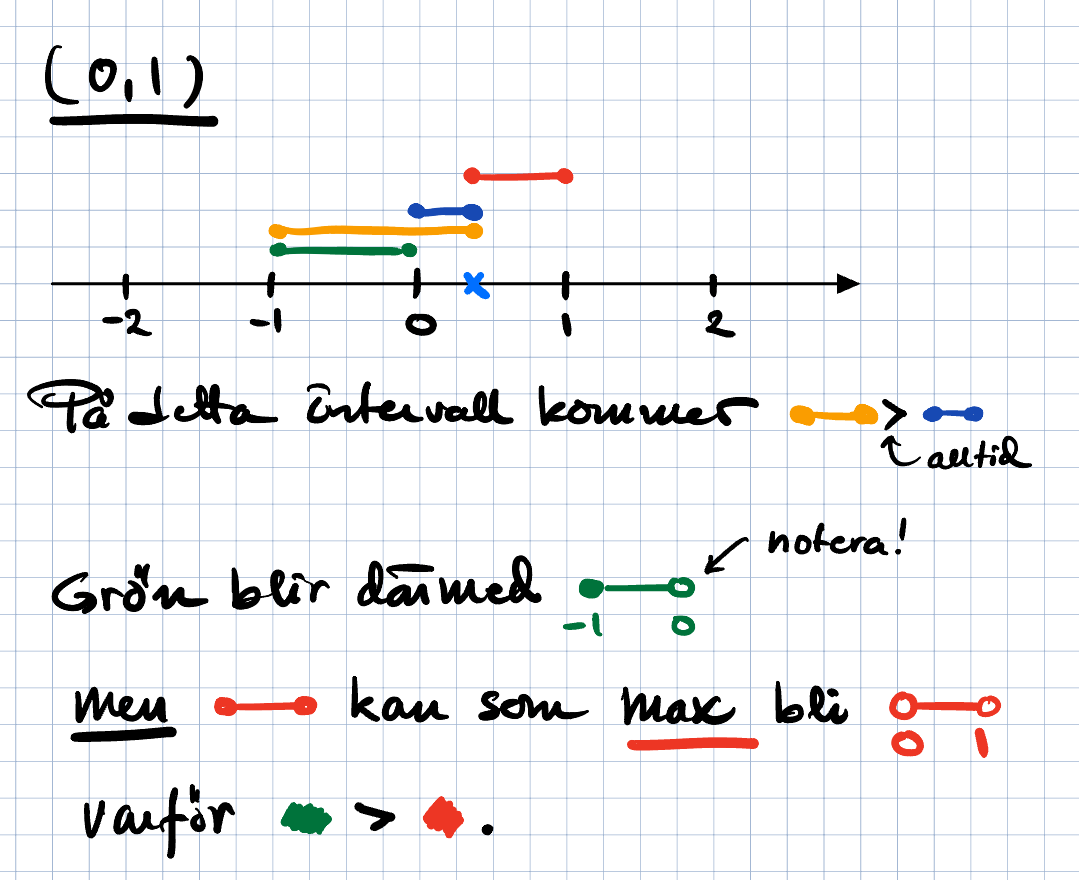
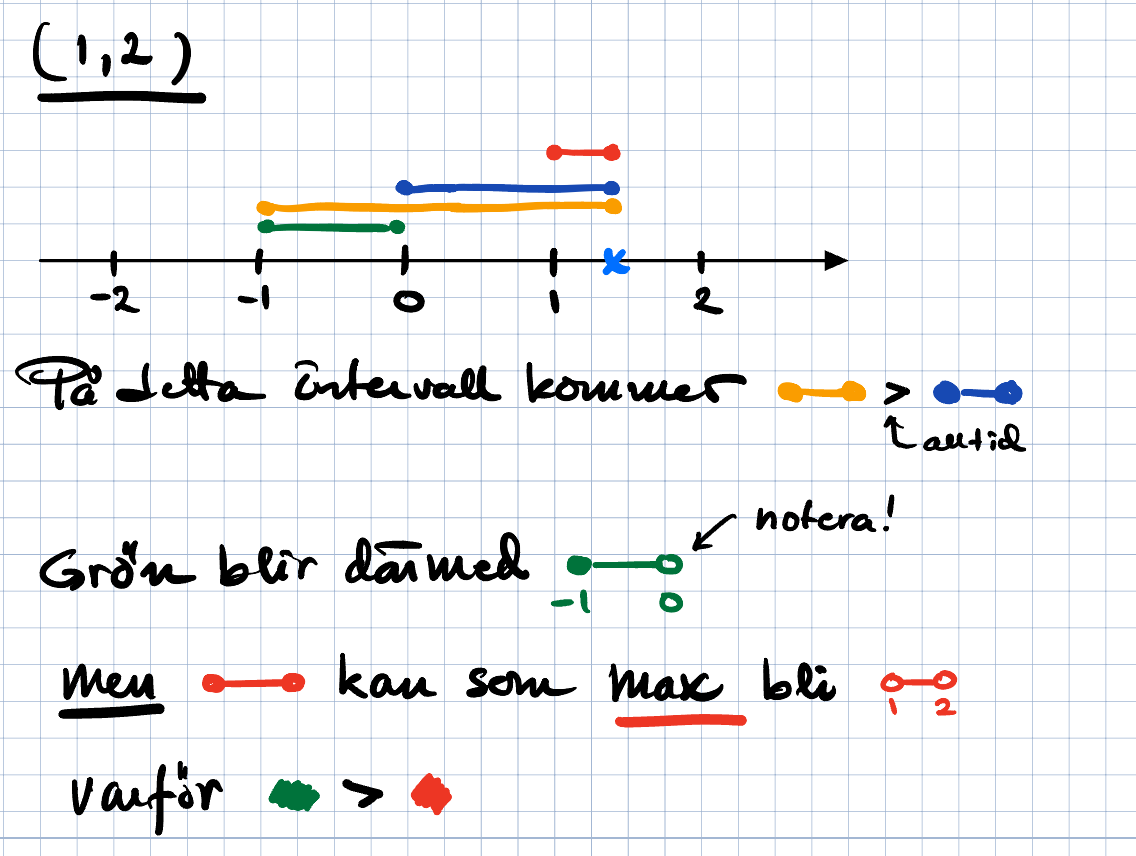
Nu tar vi absolutbeloppet av detta, och då får vi ta hand om |2x+1| i mellanintervallet. Där är brytpunkten -1/2 så vi får 1-2x, 1+2x i det intervallet, och därmed 1, 1-2x, 1+2x, 1 med intervallgränserna -1, -1/2, 0.

Sedan blandar vi in högerledet, och sen är vi snart klara. Fånigt nog inverkar den krångliga delen i mitten inte på resultatet, men det kan man inte veta innan.