Absolutbelopp

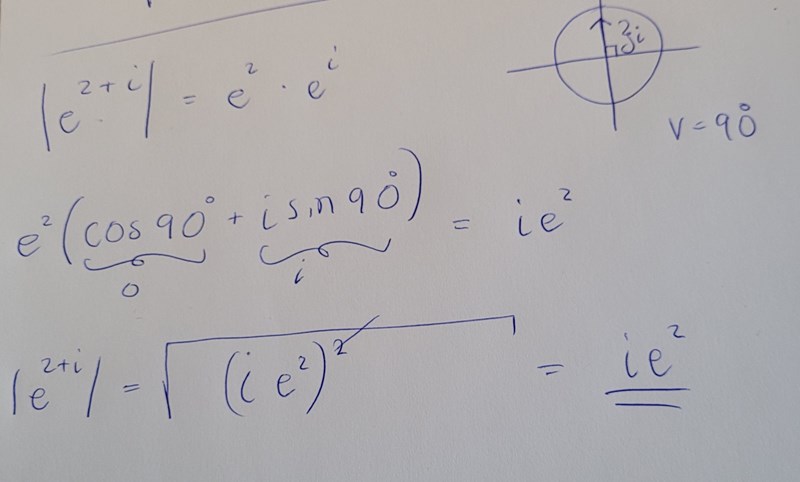 tydligen ska det bli bli bara e^2. Vad gör jag för fel?
tydligen ska det bli bli bara e^2. Vad gör jag för fel?
Hej!
Det gäller inte att , jag vet inte vart du får det ifrån. Om du vill skriva ut argumentet i exponenten så får du , så då är .
Istället kan du använda att , och beloppet av detta ges helt enkelt av . Sen spelar argumentet faktiskt ingen roll här, eftersom för något lämpligt , så att beloppet av ges av .
Hänger inte helt med. Kan du förklara det du skrev på sista raden lite mer.
offan123 skrev:Hänger inte helt med. Kan du förklara det du skrev på sista raden lite mer.
Använd att och att beloppet av ett komplext tal ges av . I ditt fall är .
Det här med radianer så här blir jag förvirrad av. Den där nollan med ett streck igenom, är det ett annat sätt att uttrycka en okänd vinkel?
Ja det är bara en vinkel. Du kanske är mer van vid istället, men det är samma sak bara olika namn på vinkeln.
 Borde man inte kunna göra nån slags identifiering?
Borde man inte kunna göra nån slags identifiering?
offan123 skrev:Det här med radianer så här blir jag förvirrad av. Den där nollan med ett streck igenom, är det ett annat sätt att uttrycka en okänd vinkel?
Det är en grekisk bokstav som heter theta (uttalas täta). Den används ofta för vinklar.
Det jag skrev på #7, är det ingen bra ide?
offan123 skrev:
Borde man inte kunna göra nån slags identifiering?
Det är en hel del som jag inte förstår vad du vill göra här. För det första så är inte det är likheten som gäller. För det andra är redan på formen , med och .
Vad är det du menar med identifiering? Hur skall det hjälpa dig att hitta absolutbeloppet?
Tänkte fel.
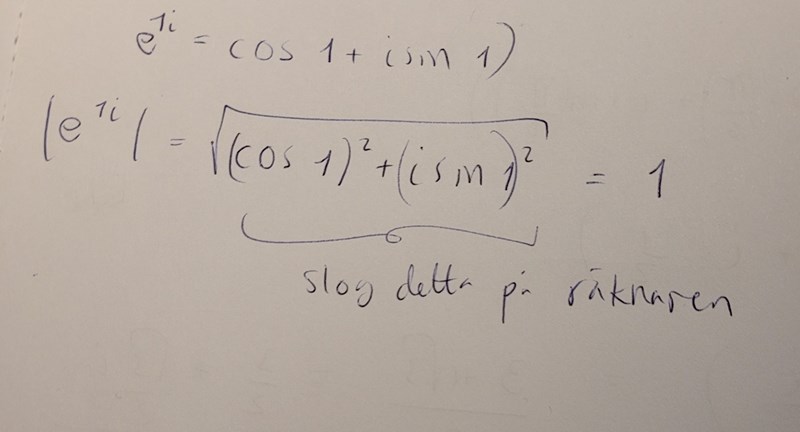 Nu undrar jag hur jag kan visa att detta blir 1. Jag kan visa på räknaren men vet ej hur man kan visa det algebraiskt.
Nu undrar jag hur jag kan visa att detta blir 1. Jag kan visa på räknaren men vet ej hur man kan visa det algebraiskt.
Eller egentligen, varför satte du vinkeln till en okänd vinkel, var det för det inte fanns någon tydlig v i eiv? Det är 1 men blir lite krångligare att räkna på.
Nej! Nu är det ungefär samma fel som jag tyckte jag såg i en annan av dina trådar. Absolutbeloppet av ett imaginärt tal ges av , det finns inget , under rottecknet. Du ska bara ta den "reella koefficienten" framför .
Om du gör så och gör rätt, så får du att eftersom du har trigonometriska ettan under rottecknet.
Nja, jag har ju skrivit att vinkeln är , så jag vet inte riktigt vad du syftar på. Oavsett så spelar inte vinkeln någon roll i det här fallet, eftersom vi ändå kommer att få trigonometriska ettan (som ju är oberoende av vinkeln).
Okej då hänger jag med. Tack för hjälpen :)


