algebra

Är inte något som blir eller hen kommer fram till utan personen definierar en ny funktion $q(x)$ vars definition är $p(x + \alpha)$Detta är i praktiken samma funktion men förskjuten längsmed x-riktningen så att istället för att minimipunkten infaller vid $x = \alpha$ så infaller den vid $x = 0$

Varför hen gör det framgår inte föränn senare beviset men det är rätt vanligt i bevis även om det kan vara lite opedagogiskt. 

Låt oss tänka oss detta med ett exempel. Säg att vi har $p(x) = x^2 -2x - 1 = (x - 1)^2 - 2$. Denna funktion har en minimipunkt i (1, -2). Om jag definierar funktionen $q(x) = p(x + 1) = x^2 - 2$ så har denna funktions graf samma form som p(x)s men q(x)s minipunkt infaller vid (0, -2) istället. 

SeriousCephalopod skrev:

Är inte något som blir eller hen kommer fram till utan personen definierar en ny funktion $q(x)$ vars definition är $p(x + \alpha)$Detta är i praktiken samma funktion men förskjuten längsmed x-riktningen så att istället för att minimipunkten infaller vid $x = \alpha$ så infaller den vid $x = 0$

Varför hen gör det framgår inte föränn senare beviset men det är rätt vanligt i bevis även om det kan vara lite opedagogiskt. 

Låt oss tänka oss detta med ett exempel. Säg att vi har $p(x) = x^2 -2x - 1 = (x - 1)^2 - 2$. Denna funktion har en minimipunkt i (1, -2). Om jag definierar funktionen $q(x) = p(x + 1) = x^2 - 2$ så har denna funktions graf samma form som p(x)s men q(x)s minipunkt infaller vid (0, -2) istället. 

tack! En annan fråga! Varför blir det e^k=-b0/bk? 

Det står på nedersta raden i stycket ovanför att de är lika.

Smaragdalena skrev:

Det står på nedersta raden i stycket ovanför att de är lika.

Jag hänger inte riktigt med. :/

"Låt e vara en lösning till ekvationen $e^k=-\frac{b_0}{b_k}$". Där står det att $e^k=-\frac{b_0}{b_k}$.

Det är alltså inte talet e=2,718281828massasiffror man menar. Olyckligt val av variabelnamn, anser jag.

Smaragdalena skrev:

"Låt e vara en lösning till ekvationen $e^k=-\frac{b_0}{b_k}$". Där står det att $e^k=-\frac{b_0}{b_k}$.

Det är alltså inte talet e=2,718281828massasiffror man menar. Olyckligt val av variabelnamn, anser jag.

Tack! Nu har förstått. Jag trodde att e =2,71 och hade svårt att förstå varför de just valde e-tal.

Jag har en till fråga. Är x = te?

Jag har en till fråga. Är x = te?

Vilken rad i beviset är det du tänker på?

Smaragdalena skrev:

Jag har en till fråga. Är x = te?

Vilken rad i beviset är det du tänker på?

Det är här som jag tänker på  eller är det bara en annan ekvation som testas med variabeln te?

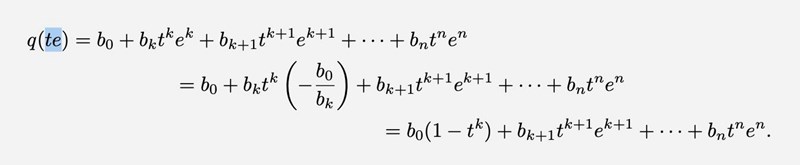
Man sätter in variablen te i funktionen q(x).

Smaragdalena skrev:

Man sätter in variablen te i funktionen q(x).

Tack för dina förklaringar. Min sista fråga är att varför abs[x+alfa] är kontinuerlig?  Är det pga abs[p(x)]?

Alla polynom är kontinuerliga och deriverbara i alla punkter. Absolutbelopp är kontinuerliga i alla punkter men har vissa punkter där de inte är deriverbara.

Smaragdalena skrev:

Alla polynom är kontinuerliga och deriverbara i alla punkter. Absolutbelopp är kontinuerliga i alla punkter men har vissa punkter där de inte är deriverbara.

Jag vill bevisa att x=0 verkligen antas. Har googlat lite och hittade satsen om mellanliggande värde (Bolzano sats) och 

INTERMEDIATE VALUE THEOREM
Let f be a polynomial function. The Intermediate Value Theorem states that if f(a) and f(b) have opposite signs, then there exists at least one value c between a and b for which f(c)=0.

Kan jag använda en av dem?