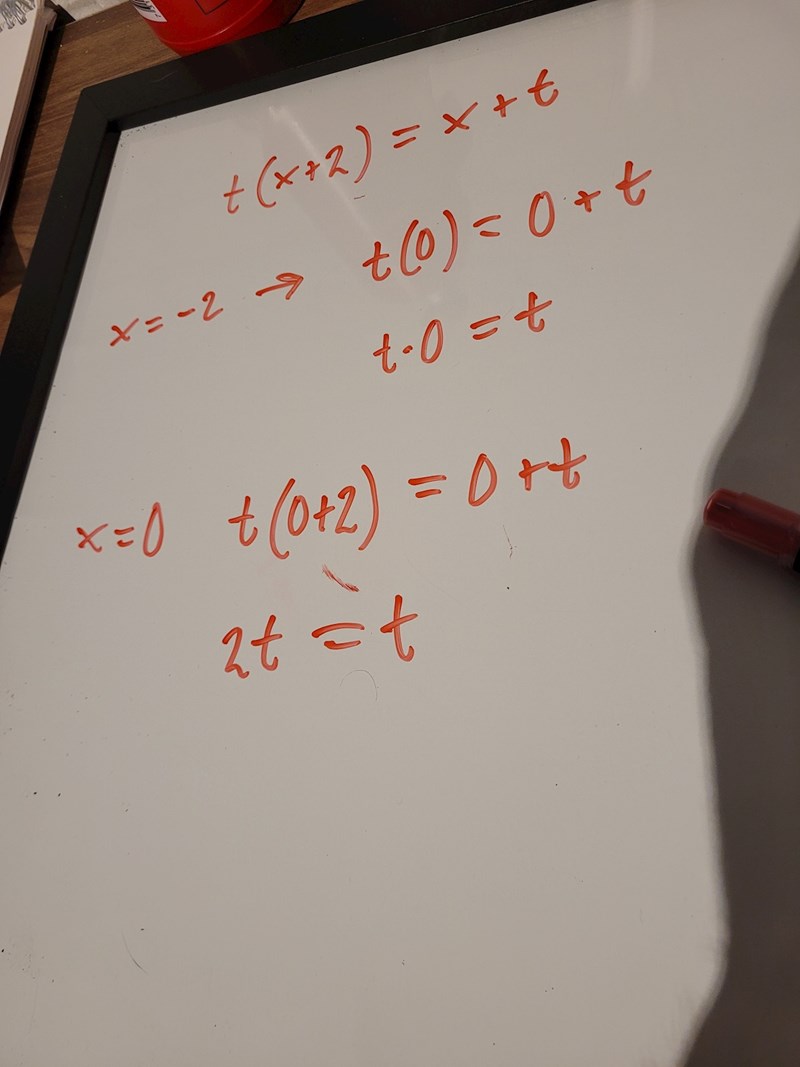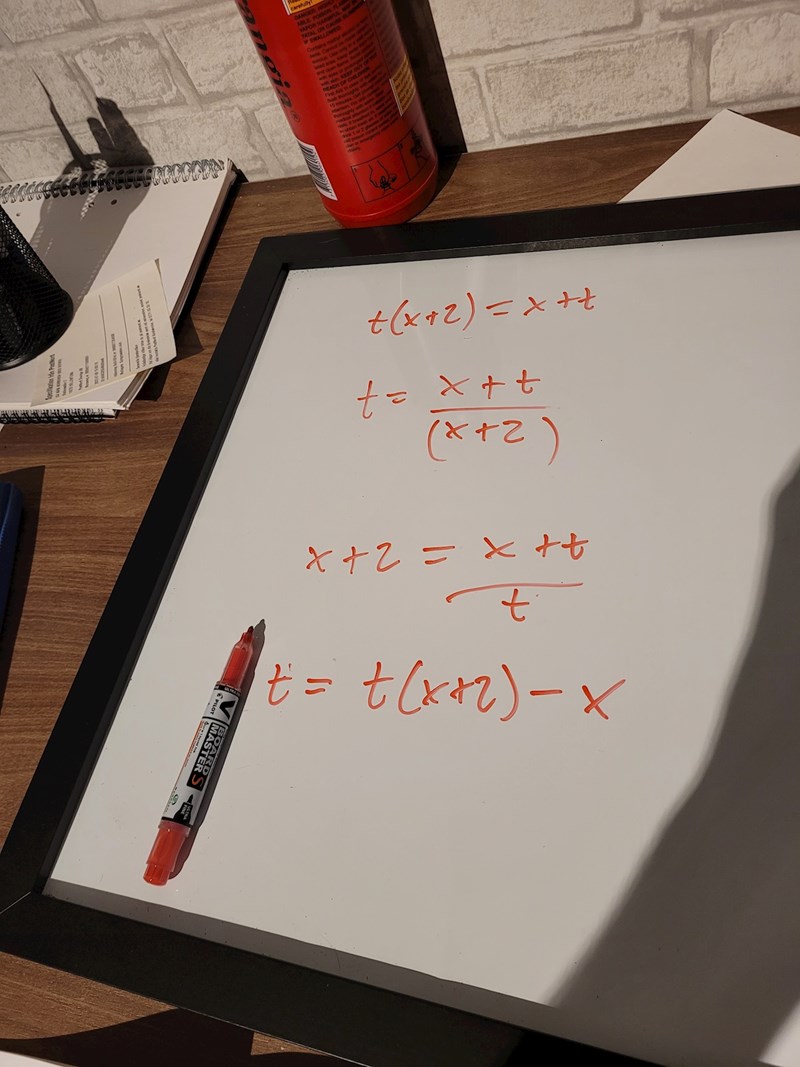Algebraiskt identitet
Jag håller på med en uppgift men jag förstår inte riktigt vad det är jag får fram och vad det svaret innebär eller om jag ens har gjort rätt. Så krångligt
För vilka värden på talet t är ekvationen en identitet?
t(x + 2) = x + t
Om jag har förståt det rätt så är en identitet en likhet som gäller för alla värden påvariablerna.
Men när jag försöker lösa denna har jag satt x som -2 och 0 Jag får typ i slutändan svaret 0t = t om jag sätter x = -2 och i ett andra försök med x = 0 så får jag t=2t.
Är något galet?
Varför väljer du just x = 0 och x = -2?
Gör istället så att du samlar alla termer på ena sidan av likhetstecknet och förenklar/faktoriserar.
Då blir det enklare att se vilket/vilka värden på t som gör att ekvationen alltid är uppfylld, oavsett vilket värde x har.
Visa dina uträkningar.
Att jag gör så är för att jag försöker följa vad exempeluppgifterna har gjort. För att få en faktor till 0 och lösa ut den andra.
StudieRo skrev:Att jag gör så är för att jag försöker följa vad exempeluppgifterna har gjort. För att få en faktor till 0 och lösa ut den andra.
x = 0 gör väl ingen faktor till 0?
Nej men den får t ensam på ena sidan.
Du kan lösa ut t ur ekvationen.
Yngve skrev:Du kan lösa ut t ur ekvationen.
Jag ser inte vart. Är det på bilden du menar?
Är ekvationen korrekt avskriven? Det finns inget t som gör att den gäller för alla x.
Jag tolkar uppgiften som att man helt enkelt ska lösa ut t ur ekvationen. Då får man fram ett t som beror av x.
Om vi använder detta t i ekvationen så bli den en identitet.
Laguna skrev:Är ekvationen korrekt avskriven? Det finns inget t som gör att den gäller för alla x.
Dubbelkollat och den är rätt.
t(x + 2) = x + t
Yngve skrev:Jag tolkar uppgiften som att man helt enkelt ska lösa ut t ur ekvationen. Då får man fram ett t som beror av x.
Om vi använder detta t i ekvationen så bli den en identitet.
Så då blir det såhär?
x = t(x + 2) - t = tx + 2t - t ---> x = tx + t
Facit säger: inga t
Nej du ska lösa ut t ur ekvationen, dvs du ska se till att t står ensamt på ena sidan av likhetstecknet.
Jag hjälper dig med att komma igång:
t(x+2) = x+t
Multiplicera in t i VL:
tx+2t = x+t
Subtrahera t från bägge sidor:
tx+t = x
Faktorisera VL:
t(x+1) = x
Kommer du vidare själv härifrån?
Jag fick precis fram den där.
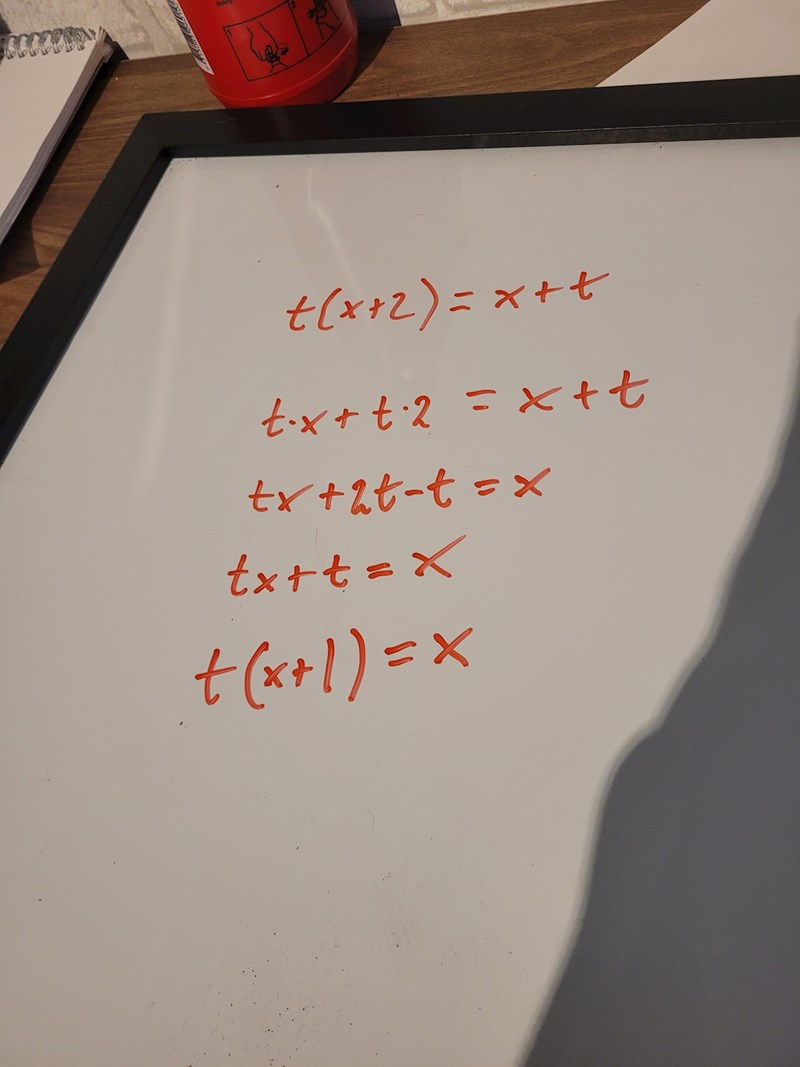
Yngve skrev:Nej du ska lösa ut t ur ekvationen, dvs du ska se till att t står ensamt på ena sidan av likhetstecknet.
Jag hjälper dig med att komma igång:
t(x+2) = x+t
Multiplicera in t i VL:
tx+2t = x+t
Subtrahera t från bägge sidor:
tx+t = x
Faktorisera VL:
t(x+1) = x
Kommer du vidare själv härifrån?
Jag ska ge mig tid o fundera lite. Tack för hjälpen!
Om jag nu använder t(x + 1) = x
Och sätter x som -1
Så blir det
t(-1 + 1) = -1
t(0)= -1
"En identitet är en likhet som gäller för alla värden på variablerna"
Hur kan jag avgöra om något är en identitet?
Testar jag genom att prova mig fram eller hur gör jag?
För visst har denna uppgift två variabler men man vill trolla med lite algebra så man bara har en?
StudieRo skrev:Om jag nu använder t(x + 1) = x
Lös ut t!
StudieRo skrev:Facit säger: inga t
Då tolkade jag tydligen uppgiften rätt.
Jag ska alltså ta fram värden på t som gör ekvationen till en identitet. En likhet mellan t och x där x kan vara vilket tal som helst?
nu sitter jag med inga t i formeln..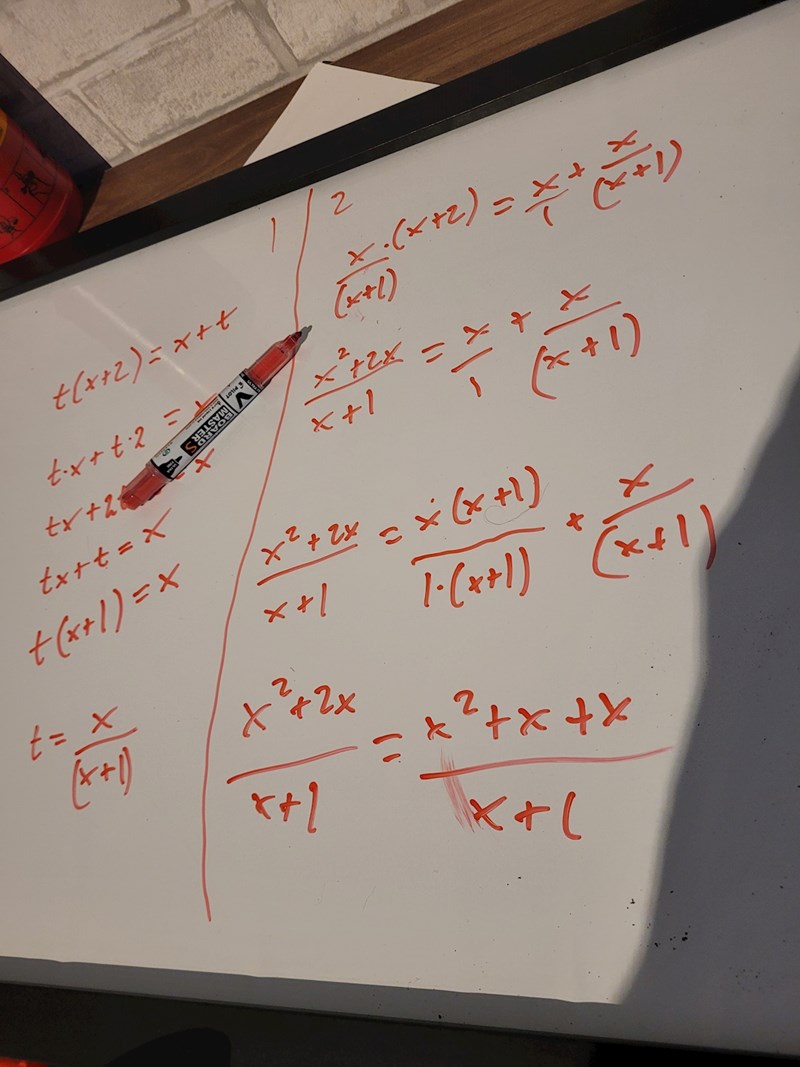
StudieRo skrev:nu sitter jag med inga t i formeln..
Ja, och du ser då att VL = HL för alla värden på x (utom x = -1). Dvs om t = x/(x+1) så är ekvationen en identitet.
Men det finns alltså inget konstant värde på t som gör ekvationen till en identitet, vilket tydligen var det som efterfrågades.
Yngve skrev:StudieRo skrev:nu sitter jag med inga t i formeln..
Ja, och du ser då att VL = HL för alla värden på x (utom x = -1). Dvs om t = x/(x+1) så är ekvationen en identitet.
Men det finns alltså inget konstant värde på t som gör ekvationen till en identitet, vilket tydligen var det som efterfrågades.
Ja men nu ser jag ju! Precis som boken visar! Tack för hjälpen! Jag har bara två korta frågor kvar, om du, eller någon annan vill svara
Att x inte får vara -1 har sin grund i att nämnaren inte ska vara 0? Bara så jag är med på noterna?
Men om det hade funnits ett värde på t som leser till identitet så hade t varit med någonstans i ekvationen?
StudieRo skrev:Att x inte får vara -1 har sin grund i att nämnaren inte ska vara 0? Bara så jag är med på noterna?
Ja, det stämmer.
Men om det hade funnits ett värde på t som leser till identitet så hade t varit med någonstans i ekvationen?
Exempel:
t(x+3) = 2x+6
Expandera VL:
tx+3t = 2x+6
Subtrahera (2x+6):
tx+3t-2x-6 = 0
Faktorisera:
(t-2)x+3(t-2) = 0
Faktorisera igen:
(t-2)(x+3) = 0
Vi ser nu att om t = 2 så är denna ekvation uppfylld för alla möjliga värden på x.
Yngve skrev:StudieRo skrev:Att x inte får vara -1 har sin grund i att nämnaren inte ska vara 0? Bara så jag är med på noterna?
Ja, det stämmer.
Men om det hade funnits ett värde på t som leser till identitet så hade t varit med någonstans i ekvationen?
Exempel:
t(x+3) = 2x+6
Expandera VL:
tx+3t = 2x+6
Subtrahera (2x+6):
tx+3t-2x-6 = 0
Faktorisera:
(t-2)x+3(t-2) = 0
Faktorisera igen:
(t-2)(x+3) = 0
Vi ser nu att om t = 2 så är denna ekvation uppfylld för alla möjliga värden på x.
Jag kan bara se en identitet om jag får en ekvation som ser ut likadant på båda leden. Vilket det gör jag om jag sätter ersätter t med två i din första ekvation.
Men om jag sätter in t=2 i sista ekvationen så får jag x=-3. Men det kanske inte är så man ska göra?
StudieRo skrev:
Jag kan bara se en identitet om jag får en ekvation som ser ut likadant på båda leden. Vilket det gör jag om jag sätter ersätter t med två i din första ekvation.
OK, bra.
Men om jag sätter in t=2 i sista ekvationen så får jag x=-3. Men det kanske inte är så man ska göra?
Nej, hur får du det?
Visa med uträkningar steg för steg hur du kommer fram till det
Yngve skrev:StudieRo skrev:Jag kan bara se en identitet om jag får en ekvation som ser ut likadant på båda leden. Vilket det gör jag om jag sätter ersätter t med två i din första ekvation.
OK, bra.
Men om jag sätter in t=2 i sista ekvationen så får jag x=-3. Men det kanske inte är så man ska göra?
Nej, hur får du det?
Visa med uträkningar steg för steg hur du kommer fram till det
Nä det är rätt. Jag tänkte fel. Det blir ju 0..
Parenteserna är ju två faktorer. Det slarvade jag med