Algebraiskt uttryck för mönsterutveckling

Hej och välkommen till Pluggakuten!

Tips: Titta på skillnaden I antal stjärnor mellan figur 1 & 2 och mellan figur 2 & 3.

Vad ser du då?

Den ökar med 3 för varje

Bra, alltså borde det algebraiska uttrycket ha något med 3 att göra. Och n som det står.

Pröva att skriva något med 3 och n och se om det passar.

det som jag kommer fram till som visar att det blir är 3n+1

Bra!

Då tänker du alltså att n = 0 för figur 1, n= 1 för figur 2, n = 2 för figur 3 o.s.v?

Oj bra fråga, tänker att figur 0 är = -2 ?

Skulle det kunna vara n+3 som är svaret?

Nej du är på helt rätt spår med 3n+1.

Och det stämmer om vi säger att första figuren har n = 0, eftersom då blir uttrycket 3*0+1 = 1, vilket stämmer med antalet stjärnor.

För andra figuren blir n = 1. Uttryckets värde är då 3*1+1 = 4, vilket stämmer med antalet stjärnor.

För tredje figuren blir n = 2. Uttryckets värde är då 3*2+1 = 7, vilket stämmer med antalet stjärnor.

====

Så ditt svar 3n+1 är helt rätt, förutsatt att du börjar på n = 0 (vilket du i så fall tydligt måste ange i ditt svar).

====

Extrauppgift: Kan du ta fram ert uttryck som stämmer om vi börjar på.n = 1 istället?

Dvs om n ör lika med figurens nummer?

Figur 1= n+1, figur 2= 2n+1, figur 3= 3n+1 ?

Jag har omtenta i matte 3 på Stockholms för grundlärare f-3, i vår portal kna man göra matte test där denna stjärnuppgift är med som test.. Jag har vid ett tillfälle skrivit att svaren är 3n+1 men i resultatet står det att det är ett felaktigt svar. Därav min förvirring :/

Zabetia skrev:

Figur 1= n+1, figur 2= 2n+1, figur 3= 3n+1 ?

 

Vi prövar om det stämmer:

• Figur 1: n = 1. Uttrycket blir då n+1 = 1+1 = 2. Det är 1 stjärna för mycket.
• Figur 1: n = 2. Uttrycket blir då n+1 = 2+1 = 3. Det är 1 stjärna för lite.
• Figur 3: n = 3. Uttrycket blir då n+1 = 3+1 = 4. Det är 3 stjärnor för lite.

Det stämmer alltså inte.

Pröva med uttrycket 3n, vad händer då?

Gör på samma sätt som jag gjorde precis nu.

Jag har omtenta i matte 3 på Stockholms för grundlärare f-3, i vår portal kna man göra matte test där denna stjärnuppgift är med som test.. Jag har vid ett tillfälle skrivit att svaren är 3n+1 men i resultatet står det att det är ett felaktigt svar. Därav min förvirring :/

Svaret är rätt om vi börjar på n = 0.

Men i det digitala testet förutsätter de troligtvis att vi börjar på n = 1 istället.

Därför fick du fel.

OK nu blir jag förvirrad, men då förstår jag att jag måste utgå från att n= 1 (i den första uppgiften) 

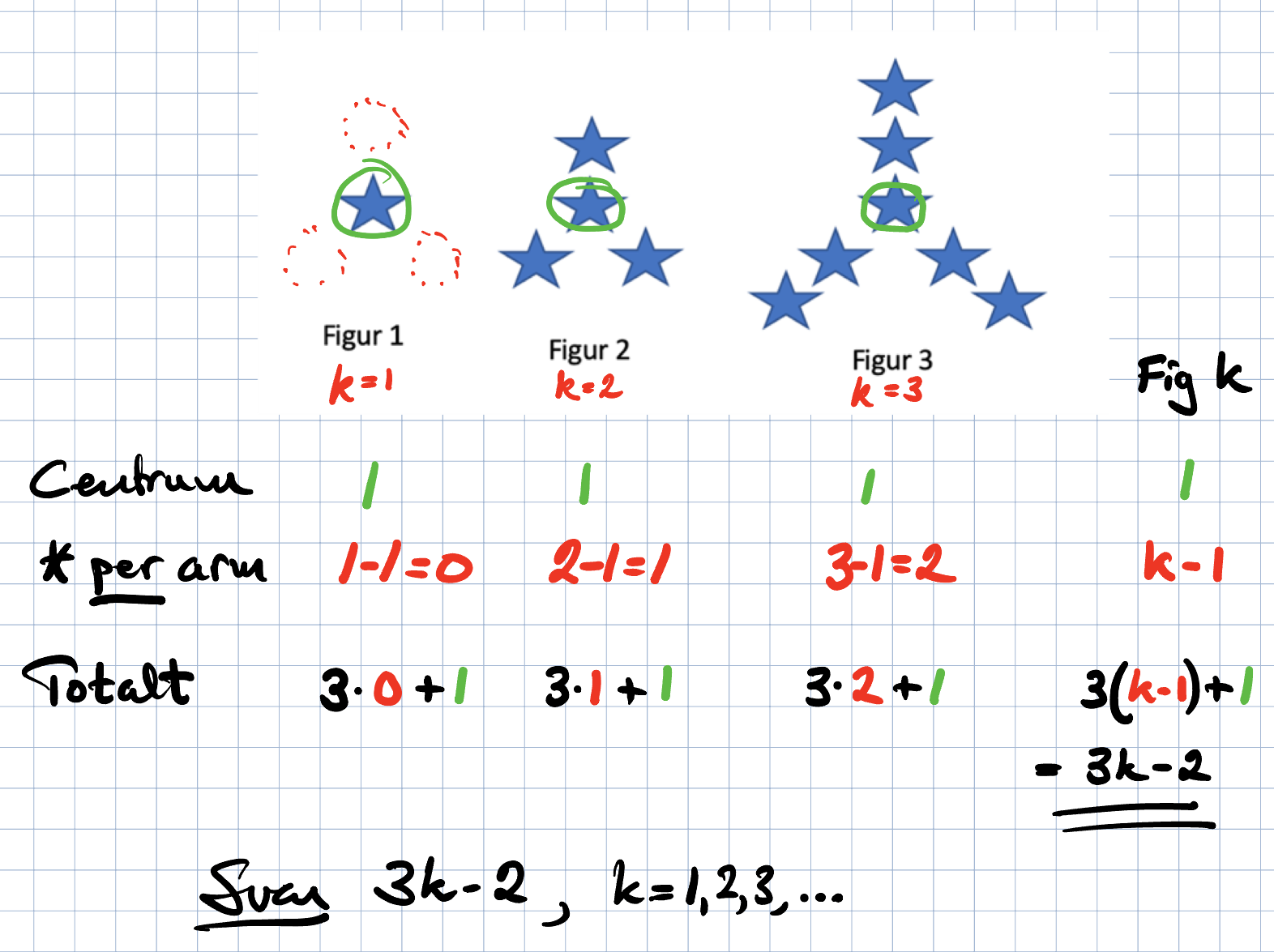
Jag vet att första bilderna innehåller 1, 4 respektive 7 stjärnor. Alltså ökar den med 3 och om det skulle finnas en figur 0 så skulle den ha -2 stjärnor. Har jag rätt så här långt? 

Hur och vad ska jag tänka på som nästa steg? För jag tror inte jag kan räkna ut ett annat exempel då jag inte har förstått ännu :)

En bra metod här är att gissa på ett uttryck, pröva om det stämmer och sedan vid behov försöka ändra uttrycket så att det stämmer.

Så här:

Vi gissar på att uttrycket är 3n, där n är figurens nummer.

Vi prövar om det stämmer;

• Om n = 1 så är uttryckets värde 3*1 = 3. Det är 2 stjärnor för mycket.
• Om n = 2 så är uttryckets värde 3*2 = 6. Det är 2 stjärnor för mycket.
• Om n = 3 så är uttryckets värde 3*3 = 9. Det är 2 stjärnor för mycket.

Vi ser att i alla tre fallen så blir uttryckets värde 2 mer än vad det ska vara. Det borde vi kunna kompensera för genom att subtrahera 2 från uttrycket.

Vi ändrar utttycket enligt analysen ovan, till 3n-2.

Ny gissning är alltså 3n-2.

Kan du nu pröva om denna gissning stämmdr, på samma sätt om jag gjorde i det här svaret?

OBS, det är viktigt att du tränar på att själv pröva om din gissning stämmer och inte bara mata in den i formuläret. 

Ja jag vill förstå :) inte bara kunna det utantill, då kommer jag inte kunna lösa det på tentan om det kommer ett annat upplägg.

Så här långt kommer jag:

n=1*1=1

2n=2*2=4

3n= Här blir det fel för 3*3 = 9 och inte 7

Vi försöker tillsammans.

Är du med på följande?

Om uttrycket är 3n-2 och

• n = 1 så blir uttryckets värde 3*1-2 = 3-2 = 1
• n = 2 så blir uttryckets värde 3*2-2 = 6-2 = 4
• n = 3 så blir uttryckets värde 3*3-2 = 9-2 = 7

Okej så för varje 3:n alltså 3 är hela tiden sen multiplicerar vi 3:an med figurens (turordnings nummer 1,2 eller 3)

Sen det svaren subtraherar vi med 2 som kommer från 3n -2?

Zabetia skrev:

Okej så för varje 3:n alltså 3 är hela tiden sen multiplicerar vi 3:an med figurens (turordnings nummer 1,2 eller 3)

Ja, är du med på att 3n betyder 3*n?

Sen det svaren subtraherar vi med 2 som kommer från 3n -2?

Ja, 3n-2 betyder 3*n-2.

Jag ber om ursäkt för att jag inte förstår så snabbt, jag vill verkligen fatta. 

Men om jag tänker på på bilden med stjärnorna och att n=1 och inte n=0 blir det då:

n =1  alltså 1*1=1

n=2 alltså 1*2=2      (här skulle det bli 4)

n= 3 alltså 1*3= 3    (här skulle det bli 7)

Nu räknar du som om uttrycket skulle vara 1*n, men det är ju 3*n-2.

Vilken mattekurs är det här?

Känner du till begreppet funktioner?

Nu tror jag att jag hänger med, har du möjligtvis en annan figur jag skulle kunna test räkna på?

Det är 3:e matte kursen för grundlärare årskurs f-3. Nej jag kommer inte ihåg det begreppet

Zabetia skrev:

Nu tror jag att jag hänger med, har du möjligtvis en annan figur jag skulle kunna test räkna på?

Japp, pröva med denna:

Det är 3:e matte kursen för grundlärare årskurs f-3. Nej jag kommer inte ihåg det begreppet

OK då förstår jag. Det är bra för oss att veta vilka förkunskaper du har eller saknar.

Zabetia skrev:

Nu tror jag att jag hänger med, har du möjligtvis en annan figur jag skulle kunna test räkna på?

Det är 3:e matte kursen för grundlärare årskurs f-3. Nej jag kommer inte ihåg det begreppet

4n+3?

figur 1= 1

figur 2=5

figur3=9 

Ökar med 4

4*1=4

4*2=8

4*3=12

+3 mellan figur och produkten = 4n+3

Zabetia skrev:

4n+3?

figur 1= 1

figur 2=5

figur3=9 

Ökar med 4

4*1=4

4*2=8

4*3=12

+3 mellan figur och produkten = 4n+3

Hej!

Yngve är offline, så jag tar vid lite.

Jag gissar du försökt hitta en funktion som beräknar hur många rutor det är i varje figur?

Jag tror vi behöver fundera lite på vad en funktion är. Se det som en fabrik, där du stoppar in ett tal och ett annat spottas ut.

Ofta brukar man skriva funktioner som exempelvis f(x), där f() betyder en funktion vi kallat f och x är det värde vi stoppar in. Bokstäverna är helt godtyckliga, även om f(x) är vanligt. Det kan vara typ rutor(n) också.

Sedan måste ju funktionen göra något också.

Vi kan hitta på en enkel funktion: f(x)=2x

I den här funktionen stoppar du in ett tal x och ut får du ett annat, nämligen värdet av f(x). Vad funktionen gör se du på högersidan av likhetstecknet, den tar x gånger 2.

Stoppar vi in x=2, så får vi ut f(2)=2*2=4.
Stoppar vi in x=3, så får vi ut f(3)=2*3=6.

Det sådana här uppgifter med figurer handlar om är att vi skall hitta en funktion, där vi stoppar in figurnumret och ut skall vi få antalet kvadrater i det här fallet (eller stjärnor i din ursprungliga).

Figurnumret kallar vi n i det här fallet, men det kan förstås vara x också. Det spelar ingen roll.

Givet bilden så vet vi att om vi stoppar in figurnumret 1, alltså n=1, så skall värdet av funktionen bli 1 (kvadrat).
Stoppar vi in figurnumret 2, skall vi får ut en 5:a. Till sist vet vi att n=3 skall bli 8.

Vi vet alltså följande:

• f(1)=1
• f(2)=5
• f(3)=9

Det vi stoppar in, alltså figurnumren 1, 2 och 3, benämner vi n. Funktionen kallar vi f(n).

Det vi skall klura ut är vad som skall stå på högersidan av likhetstecknet. Vad skall vi göra med n för att resultatet skall bli 1, 5, respektive 9 när vi stoppar in 1, 2, respektive 3?

f(n)=[en beräkning som innehåller n]

Säger vi att f(n)=4n+3, så ser vi att f(1)=4*1+3=7. Det fungerar inte alls. Vi har inte 7 kvadrater i första figuren, utan enbart en enda.

Däremot har du korrekt identifierat att varje figur växer med 4 kvadrater varje gång.

Låt oss prova med f(n)=4n, för då kommer det ju att bli 4 fler varje gång. 

f(1)=4*1=4
f(2)=4*2=8
f(3)=4*3=12

Det växer med 4 varje gång, så det är åt rätt håll åtminstone även om det är för många.

Vi justerar funktionen lite: 

f(n)=4(n-1)

f(1)=4(1-1)=4*0=0
f(2)=4(2-1)=4*1=4
f(3)=4(3-1)=4*2=8

Den växer också med fyra, men det saknas en kvadrat varje gång.

Vi justerar igen:

f(n)=4(n-1)+1

f(1)=4(1-1)+1=4*0+1=1
f(2)=4(2-1)+1=4*1+1=5
f(3)=4(3-1)+1=4*2+1=9

Nu är vi hemma! 

4(n-1)+1 verkar vara det samband vi söker, där n är figurens nummer och värdet av 4(n-1)+1 är antalet kvadrater i figuren.

Sedan kan vi ju snygga till funktionen lite om vi vill:

f(n)=4(n-1)+1
f(n)=4n-4+1
f(n)=4n-3

Det är ju nästan vad du hade kommit fram till, förutom att ditt +3 har blivit -3.

Var förklaringen för omständlig, så hoppas jag du har överseende.

Kika även här: Funktionsbegreppet - Matteboken