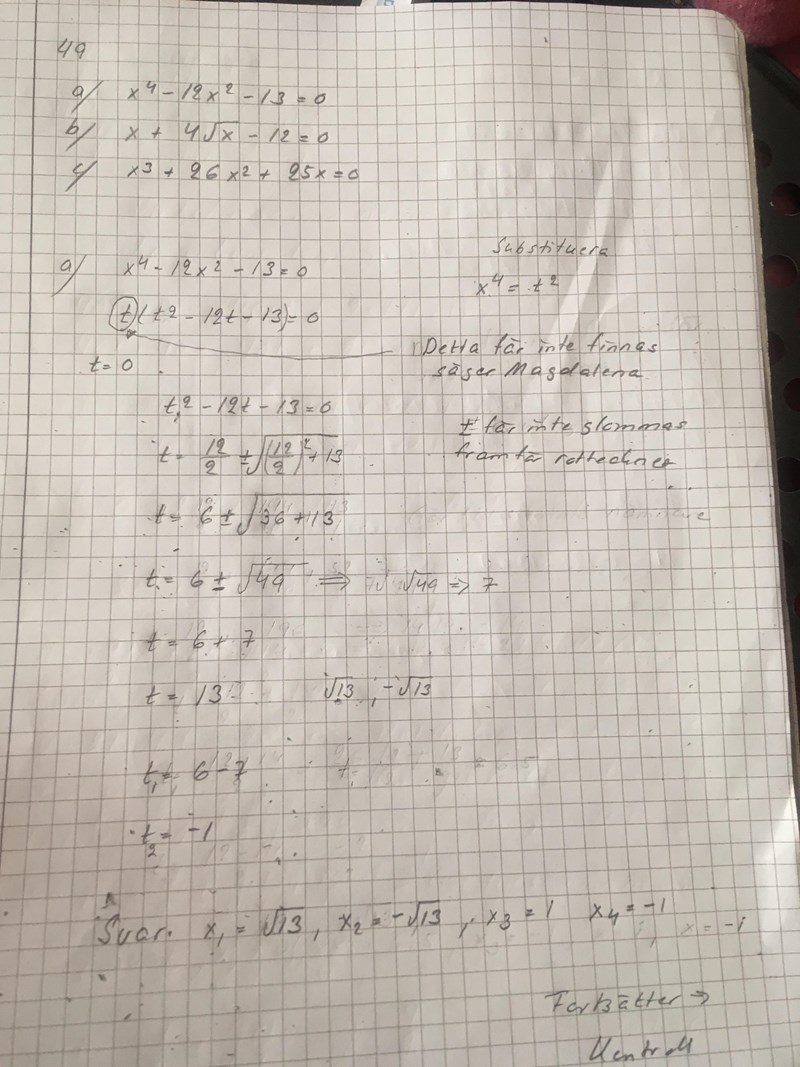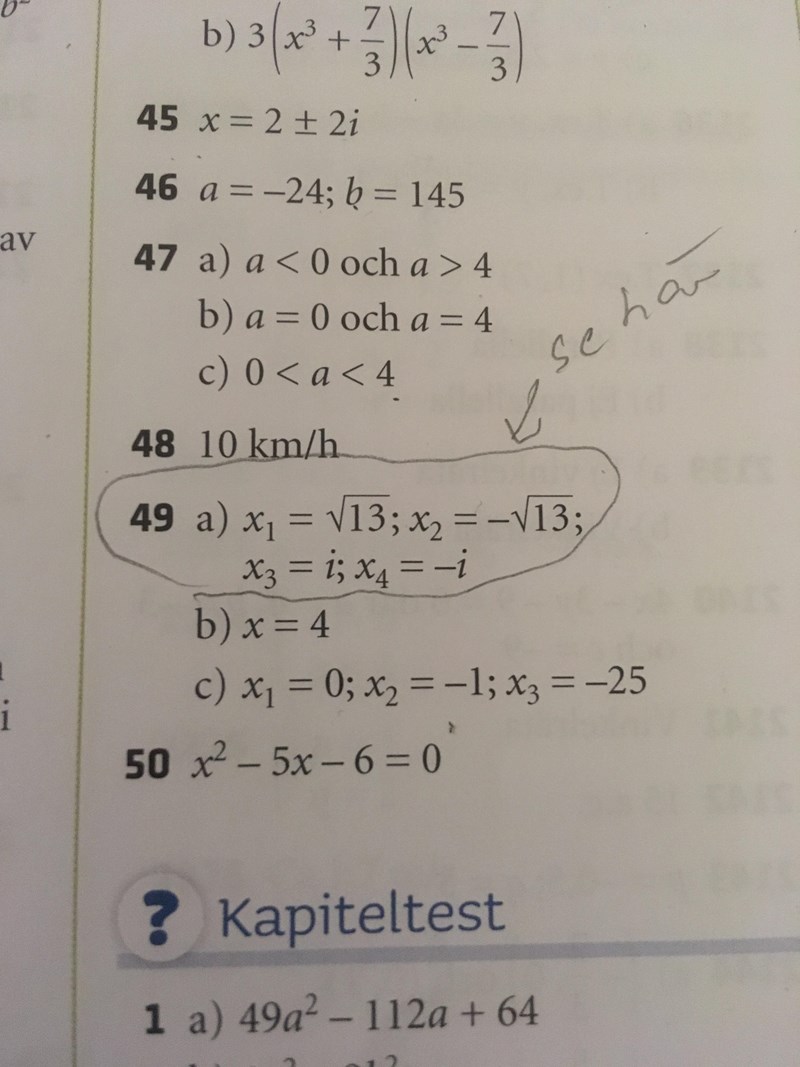Alla får hjälpa som vill
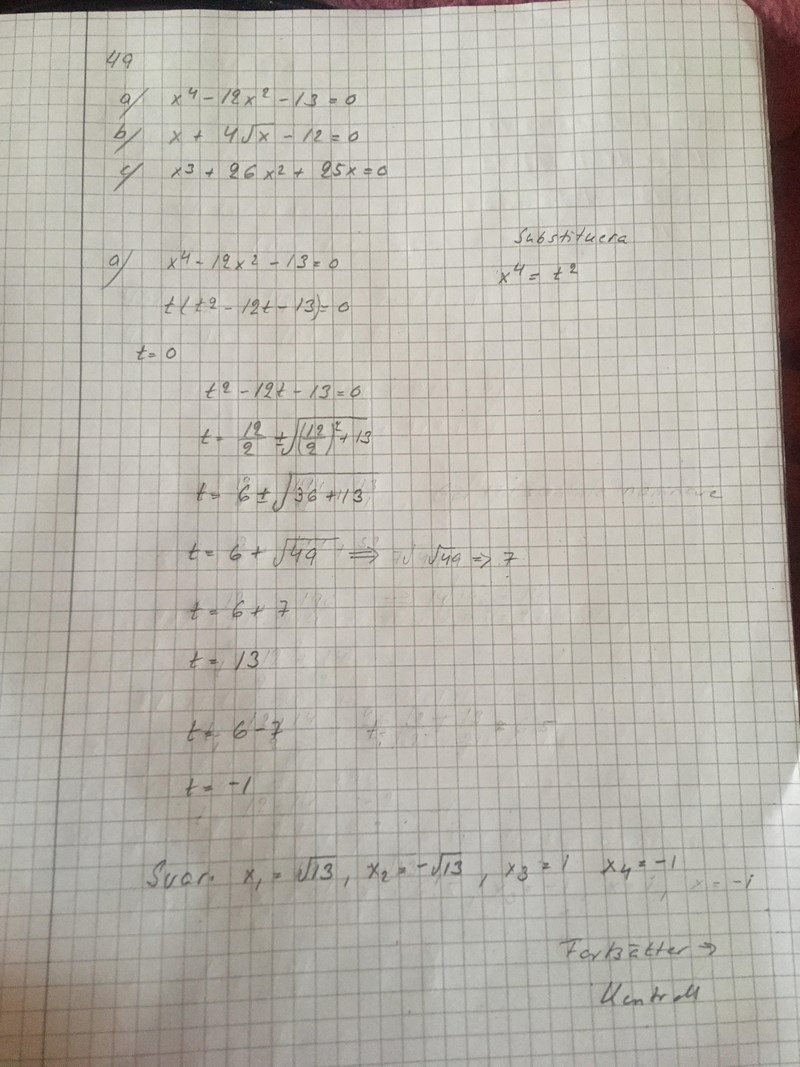
 Behöver hjälp kontrollera att svaren stämmer när det gäller fjärde grads ekvation som innehåller komplexa. Det här är inte jag säker på ännu.
Behöver hjälp kontrollera att svaren stämmer när det gäller fjärde grads ekvation som innehåller komplexa. Det här är inte jag säker på ännu.
Hur gör man detta med fjärde grads ekvation?
Inga påpekanden. Behöver hjälp med detta.
Först, du har kommit fram till rätt svar.
Sen vill du kontrollera svaren, mycket bra. Du tar bara ett av de möjliga x:en i taget och sätter in i ursprungsekvationen
Tex kan vi testa x=
Så det är korrekt.
Låt oss testa x=i
Ja, det stämmer också. 2 st x kvar att testa
Vad menar du med "inga påpekanden"? Vill du ha hjälp, eller vill du inte ha några påpekanden om vad som är fel?
Jag chansar på att du vill ha korrigeringar på det som är fel.
Du har ett felaktigt t framför parentesen just när du har gjort substitutionen. Det skall bort, liksom t = 0 på raden under. Om du stoppar in t = 0 ser du att VL inte är lika med HL, så t = 0 är ingen lösning (inte x = 0 heller).
Sedan ser det bra ut en bit. Du tappar bort plusminus på en rad, men sedan räknar du med båda varianterna och får fram två lösningar för t. Det vore tydligare om du skriv index på de båda lösningarna.
När du går tillbaka från t till x gör du rätt på de lösningarna som motsvarar t = 13 men fel på lösningarna som motsvarar t = -1. Om du sätter in dina fyra lösningar i ursprungsekvationen märker du vilka som stämmer eller inte. Du skall alltså sätta in dina fyra värden i fjärdegradsekvatione, inte i den där du har bytt ur x-kvadrat mot t.
Nej, jag menar att man ska inte komma säga till mig att du får repetera om komplexa. Nu vill ja ha hjälp med att kunna kontrollera. Övriga påpekanden är godkända anser jag. Det har jag inget emot alls.
Detta gjorde en annan tidigare till mig.
Päivi skrev :Nej, jag menar att man ska inte komma säga till mig att du får repetera om komplexa. Nu vill ja ha hjälp med att kunna kontrollera. Övriga påpekanden är godkända anser jag. Det har jag inget emot alls.
Detta gjorde en annan tidigare till mig.
Det är bra att du är tydlig med vilken typ av återkoppling du vill/inte vill ha Päivi.
Tips: Skriv alltid det i trådstarten.
-------------
Om uppgiften;
Du gör substitutionen , löser ekvationen korrekt och kommer fram till rötterna och .
Eftersom så gäller att och det är när du nu ska substituera tillbaka som det blir fel.
ger och
ger och , dvs och
Smaragdalena skrev :Vad menar du med "inga påpekanden"? Vill du ha hjälp, eller vill du inte ha några påpekanden om vad som är fel?
Jag chansar på att du vill ha korrigeringar på det som är fel.
Du har ett felaktigt t framför parentesen just när du har gjort substitutionen. Det skall bort, liksom t = 0 på raden under. Om du stoppar in t = 0 ser du att VL inte är lika med HL, så t = 0 är ingen lösning (inte x = 0 heller).
Sedan ser det bra ut en bit. Du tappar bort plusminus på en rad, men sedan räknar du med båda varianterna och får fram två lösningar för t. Det vore tydligare om du skriv index på de båda lösningarna.
När du går tillbaka från t till x gör du rätt på de lösningarna som motsvarar t = 13 men fel på lösningarna som motsvarar t = -1. Om du sätter in dina fyra lösningar i ursprungsekvationen märker du vilka som stämmer eller inte. Du skall alltså sätta in dina fyra värden i fjärdegradsekvatione, inte i den där du har bytt ur x-kvadrat mot t.
Jag har korrigerat detta Magdalena! Tack för de hör påpekanden. Tycker bra om sådant här
Hej Päivi.
Nu blev det fel. Du ersätter med när du kontrollerar lösningen (blåkryssat). Det stämmer inte.
Det som gäller är att . Para alltså ihop i-faktorerna två och två på följande sätt:
-termen:
-termen:
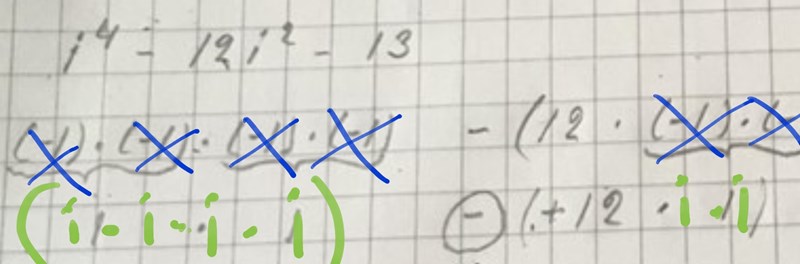
Tusen tack för detta. Tackar Magdalena, Joculator och Yngve för allt detta.
Hej Päivi. Ditt extra t framför parentesen på rad två gör att rad 1 och rad två beskriver två helt olika ekvationer, med olika lösningar.
Ekvationen på rad två har en lösning som är t = 0, dvs x = 0 (vilket du också har skrivit, men som du sedan inte fortsätter att analysera). Men x = 0 är inte en lösning till ekvationen på rad 1, vilket du enkelt kan kontrollera.
Ekvationerna är alltså olika, med olika lösningar.
Det ska inte vara något t framför parentesen på rad två.

Ja, jag tyckte att du borde repetera om du verkligen menade vad du skrev. Du hade nämligen blandat ihop talet -1 med imaginära enheten i.
Det tyckte du uppenbarligen inte om, men nu har du ju gjort exakt samma fel i den här tråden.
Om - och jag skriver OM - du har svårt att skilja på de två, så behöver du repetera komplexa tal.
Hej Päivi. Det står fortfarande fel på första papperet, när du substituerar tillbaka från till (rödmarkerat).
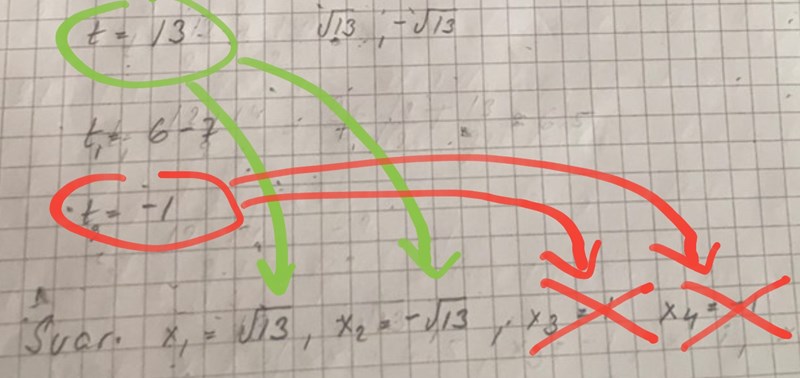
Hej Päivi. Det står även fel överst på andra papperet (rödkryssat).
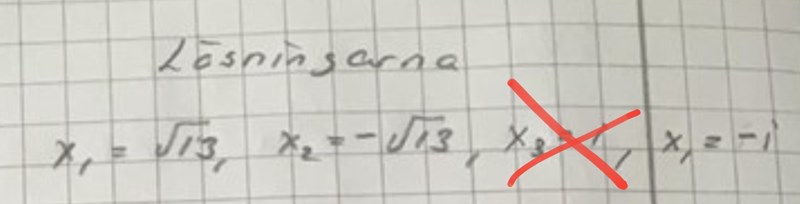
Hej Päivi. Det står fortfarande samma fel på rad 2.

Jag hade elbolag här. Jag kom bort ett tag från matten helt.
Hej Päivi.
Det här stämmer fortfarande inte.
Det gäller att och alltså att
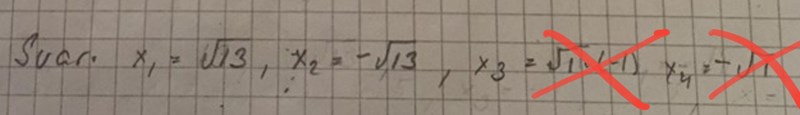
Yngve skrev :Hej Päivi. Det står fortfarande samma fel på rad 2.
Såg du inte Yngve, vad jag skrev vid sidan om att den får inte finnas där. Det är bättre att det står så att det var Magdalena som påpekade om det. Då vet jag att den för inte finnas där och att detta inte upprepas. Jag skrev särskild om att Magdalena påpekade .
Hej Päivi. Det första exenplet stämmer: , men det andra exemplet dtämmer inte, dvs ,

Det finns inte mycket om komplexa i min bok. Det är minimalt sådant.
-1 ska ska skrivas roten -1 eller - roten minus 1. Det är lättare skriva +/- istället och roten ur. Nu förstår jag inte, hur man ska kunna substituera tillbaka det där. Då låter jag bli substituera i forsättningen. Det där verkar vara väldigt störande moment.
Nu vet jag inte, hur det ska vara.
Päivi skrev :Yngve skrev :Hej Päivi. Det står fortfarande samma fel på rad 2.
Såg du inte Yngve, vad jag skrev vid sidan om att den får inte finnas där. Det är bättre att det står så att det var Magdalena som påpekade om det. Då vet jag att den för inte finnas där och att detta inte upprepas. Jag skrev särskild om att Magdalena påpekade .
Jo det såg jag. Men efrersom du försöker rätta de andra felen i dina uträkningar så trodde jag att du skulle rätta även detta.
Jag var tvungen skriva särskild att det var Magdalena som påpekade mig om detta att det får inte finnas där. Det kan vara bra på det viset att detta inte upprepas.
Är detta bättre nu, Yngve?
Päivi skrev :Nu vet jag inte, hur det ska vara.
Det har jag förklarat i detta svar. Har du inte läst det?
Yngve skrev :Päivi skrev :Nej, jag menar att man ska inte komma säga till mig att du får repetera om komplexa. Nu vill ja ha hjälp med att kunna kontrollera. Övriga påpekanden är godkända anser jag. Det har jag inget emot alls.
Detta gjorde en annan tidigare till mig.
Det är bra att du är tydlig med vilken typ av återkoppling du vill/inte vill ha Päivi.
Tips: Skriv alltid det i trådstarten.
-------------
Om uppgiften;
Du gör substitutionen , löser ekvationen korrekt och kommer fram till rötterna och .
Eftersom så gäller att och det är när du nu ska substituera tillbaka som det blir fel.
ger och
ger och , dvs och
Kunde man inte skriva på direkten - i och i, Yngve. Jag tyckte att jag skrev så och därför begrep jag inte, vad som var fel med det. Mina i kan likna ibland som ettor.
Om dina i ser ut som ettor måste du vara petigare med att sätta en prick över dem. Gissa varför jag började göra tvärstreck på mina z när jag räknar matte?
Liknade de tvåor Magdalena? Mina i kan likna ettor ja.
Ja, precis - det som var blev helt plötsligt och det tog en evinnerlig tid innan jag hittade vad det var jag hade gjort fel!
Päivi skrev :Kunde man inte skriva på direkten - i och i, Yngve. Jag tyckte att jag skrev så och därför begrep jag inte, vad som var fel med det. Mina i kan likna ibland som ettor.
Gör tydligare skillnad på i och 1 i fortsättningen.
Du skapar onödigt arbete för oss och onödig förvirring för dig själv.
Jag ska försöka med det, Yngve!