Amplitude probability density function i Matlab

Sannolikheten mellan a och b får du om du integrerar din funktion $p\left(x\right)$ från a till b enligt:

$\displaystyle P\left(a<X\leq b\right)=\int_{a}^{b}p\left(x\right) dx$

Du vet om att det är en normalfördelning? Du har integrerat täthetsfunktionen du konstruerade med hjälp av den inbyggda trapetsregeln trapz i Matlab. Det enda spåret av ursprungsdatan i det läget är standardavvikelsen du beräknade med std-funktionen.

Är datan i "Bearing.mat" verkligen kontinuerlig? Kan du ge mer information? Kanske lägga upp bilder på några plots...

Ebola skrev:

Sannolikheten mellan a och b får du om du integrerar din funktion $p\left(x\right)$ från a till b enligt:

$\displaystyle P\left(a<X\leq b\right)=\int_{a}^{b}p\left(x\right) dx$

Du vet om att det är en normalfördelning? Du har integrerat täthetsfunktionen du konstruerade med hjälp av den inbyggda trapetsregeln trapz i Matlab. Det enda spåret av ursprungsdatan i det läget är standardavvikelsen du beräknade med std-funktionen.

Är datan i "Bearing.mat" verkligen kontinuerlig? Kan du ge mer information? Kanske lägga upp bilder på några plots...

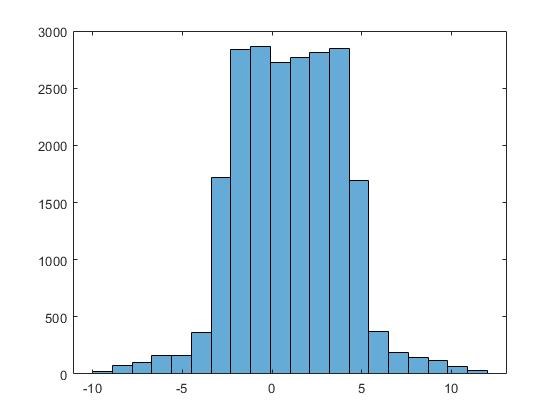
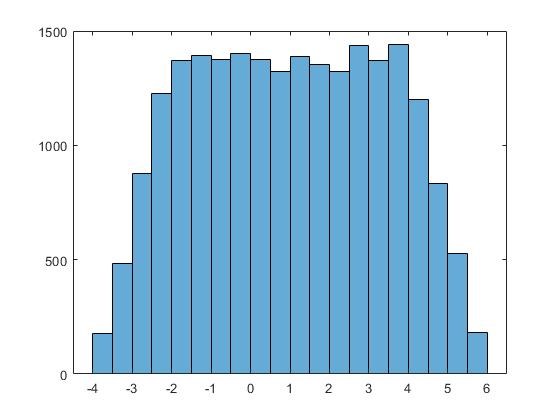
Båda första bilderna är från Bearing.mat som har två olika info. Och den är fördelad i 20 eftersom uppgifter ville ha i 20. För standardavvikelse är lite osäkert ifall jag har tagit från rätt information. Kan kopiera uppgiften så du förstår vad de handlar om.

1.3. Amplitude probability density functions
Load the file “Bearing.mat” that contains two signals of rotating machinery. One of the
signals contains a faulty bearing and one is from a healthy machine.

Assignments:

1. Calculate the probability density functions for the signals in MATLAB using the
histogram “hist” command. Plot the probability density functions as bar plots
with at least 20 segments. What is the value of the peak in the plot? Verify that the
total probability is one.

2. Calculate the skewness and kurtosis of the signals. From these quantities determine
which of the bearings you suspect is faulty. Describe how you reached your
conclusion.

Oj, wow, vilken spännande uppgift.

Jag undrar varför de vill att man ska använda hist-funktionen egentligen, den rekommenderas inte längre i MATLAB efter rev. 2014b. Du kan hursomhelst läsa denna tråd för tips:

How can we calculate probability density of a histogram?

Jag hoppas det hjälper dig. Jag har inte tid att titta mer specifikt nu och får återkomma imorgon om du behöver mer hjälp.

Ebola skrev:

Oj, wow, vilken spännande uppgift.

Jag undrar varför de vill att man ska använda hist-funktionen egentligen, den rekommenderas inte längre i MATLAB efter rev. 2014b. Du kan hursomhelst läsa denna tråd för tips:

How can we calculate probability density of a histogram?

Jag hoppas det hjälper dig. Jag har inte tid att titta mer specifikt nu och får återkomma imorgon om du behöver mer hjälp.

Jag kan vänta tills imorgon ifall jag löser inte idag. Jag tror de har bara missat uppdatera funktionen, de bruka använda samma uppgift för varje kursomgång  och förmodligen har dom missat ändra matlab koden.

Btw, de blev så här nu de länken du har skickat.

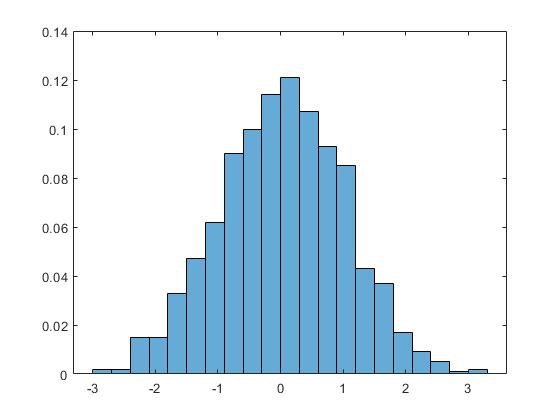
Tog bort dina skrikiga versaler. Det står i Pluggakutens regler (och i rutan där du skriver in rubriken) att du skall undvika att skriva rubriken med endast stora bokstäver. /moderator

AstridG skrev:

Har det här histogrammet något att göra med de tidigare två?

Dr. G skrev:

AstridG skrev:

Har det här histogrammet något att göra med de tidigare två?

När du säger det, så glömde jag göra det separat. Eftersom det är två olika signaler som filen ger så fick jag byta variabeler så de bilda två separata resultat. 

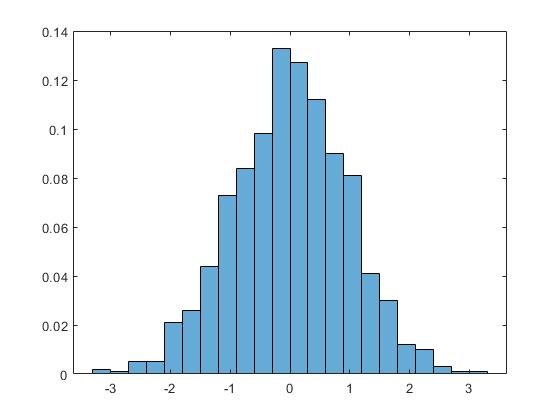
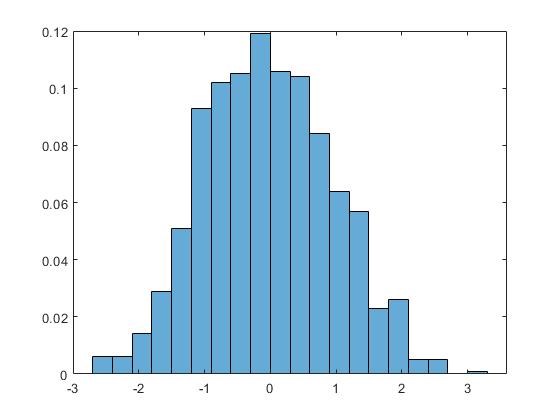
Menar du att de två senaste histogrammen och de två första i tråden beskriver samma data?

Vad är det på x-axeln i de två fallen? 

De senare histogrammen ser ut att komma från hyfsat normalfördelad data, men inte de två första. 

Dr. G skrev:

Menar du att de två senaste histogrammen och de två första i tråden beskriver samma data?

Vad är det på x-axeln i de två fallen? 

De senare histogrammen ser ut att komma från hyfsat normalfördelad data, men inte de två första. 

dom två första fallet är från

histogram(A.Bearing1, 20)
histogram(A.Bearing2, 20)

och mätte upp the peak, problemet är att jag vet inte hur jag ska bevisa att båda integral av p(x) med intervall oändlighet negativ och positiv är lika med 1. (är inte alls duktigt med matlab, så du vet). x-axis borde va duration om jag har förstått rätt.  

Du kan läsa här för att ta reda på hur du bestämmer arean i din plot:

Calculate area under histogram

Om man kikar på dina bilder övergripande så kan jag snabbt säga att det ser ut som om arean är 1 för båda plots.