Analys: en förmodan om kruvor och normallinjer

Jag är inte säker på att jag hänger med. Varför skulle det krävas att normalen antar samma lutning i två olika punkter?

Ta kurvan som definieras av $y=x^2$. Denna har olika lutning i alla punkter (och alltså har även normalen det). Fast "omfånget" blir väl ändå $\mathbb{R}^2$?

Jo i fallet y=x^2 så närmar sig lutningen samma tal (noll) i ändarna. Jag skrev inte det men det får inkluderas då.

Men ditt exempel motsäger ändå inte min förmodan faktiskt. Omfånget är R2 om den antar samma lutning i två olika punkter. (Det finns inte "om och endast om)

Jag kan inte komma på någon kontinuerlig funktion som inte har "omfång" ${\mathrm{ℝ}}^2$. Eller menar du utåtriktad normal, kanske? Alltså bara ena sidan av normalen i riktning med gradienten för funktionen i den punkten?

Ebola skrev:

Jag kan inte komma på någon kontinuerlig funktion som inte har "omfång" ${\mathrm{ℝ}}^2$. Eller menar du utåtriktad normal, kanske? Alltså bara ena sidan av normalen i riktning med gradienten för funktionen i den punkten?

En kvartsscirkel?

Och det är valfri kurva, måste inte vara en funktionskurva.

Qetsiyah skrev:

En kvartsscirkel?

Och det är valfri kurva, måste inte vara en funktionskurva.

Ah, då är jag med på vad du menar. Kul!

Jo, men vad jag menar är: har inte alla deriverbara kurvor $\mathbb{R}^2$ som omfång, oavsett om normalen antar samma lutning i två olika punkter?

EDIT: Jag ser nu att du tycks mena något annat med $k:\mathbb{R}\to\mathbb{R}^2$ än det jag tolkar det som. Vad menas egentligen med att definitionsmängden är $\mathbb{R}$?

AlvinB skrev:

Jo, men vad jag menar är: har inte alla deriverbara kurvor $\mathbb{R}^2$ som omfång, oavsett om normalen antar samma lutning i två olika punkter?

Nej, ett valfritt cirkelsegment som är kortare än en halvcirkel har väl inte det?

AlvinB skrev:

EDIT: Jag ser nu att du tycks mena något annat med $k:\mathbb{R}\to\mathbb{R}^2$ än det jag tolkar det som. Vad menas egentligen med att definitionsmängden är $\mathbb{R}$?

Öh jag venne, typ att den är parametriserad av något och att outputen är en punkt R2. Då skrivs det väl så?

Om det nu bara kan vara ett kort kurvsegment, duger inte ett segment av en rät linje som motexempel? Den har samma lutning i alla dess punkter, men så länge segmentet är ändligt blir omfånget inte $\mathbb{R}^2$.

Oj herregud vad jag är dum. Jamen rät får den inte vara såklart.

Kul fråga! Det finns ju en del detaljer man direkt kan börja fundera på, t.ex. vad vi menar med en 'kurva' (endimensionell mångfald kanske är det mest generella vi kan dra till med?), och om vi på något vis vill att kurvan ska vara så pass deriverbar att den har en normal i alla punkter, eller om vi accepterar kontinuerliga kurvor som endast har en normal i vissa punkter.

Precis som AlvinB påpekar förefaller det som att ett linjesegment är ett motexempel mot förmodan, så som den är formulerad nu, så att normalen har samma lutning i två distinkta punkter är nog inte ett tillräckligt vilkor för att kurvans omgång ska bli $\mathbb{R}^2$. Däremot är det kanske ett nödvändigt vilkor? 

Bara för att ha något att utgå från, så tänker jag att en cirkel väl alltid har hela $\mathbb{R}^2$ som omgång, vilket väl mer generellt även gäller för alla slutna och tillräckligt släta ($C^1$ borde väl räcka) kurvor? Så där har vi ett tillräckligt vilkor, men det är knappast nödvändigt, eftersom ju normalerna till en sluten slät kurva väl täcker hela $\mathbb{R}^2$ minst två gånger... 

oggih skrev:

Kul fråga! Det finns ju en del detaljer man direkt kan börja fundera på, t.ex. vad vi menar med en 'kurva' (endimensionell mångfald kanske är det mest generella vi kan dra till med?), och om vi på något vis vill att kurvan ska vara så pass deriverbar att den har en normal i alla punkter, eller om vi accepterar kontinuerliga kurvor som endast har en normal i vissa punkter.

Det måste ju åtminstone vara intervall där det finns normaler, enstaka vill vi väl inte ha. Den täcker ju ingenting av R2 då? (Måtteori igen...)

Precis som AlvinB påpekar förefaller det som att ett linjesegment är ett motexempel mot förmodan, så som den är formulerad nu, så att normalen har samma lutning i två distinkta punkter är nog inte ett tillräckligt vilkor för att kurvans omgång ska bli $\mathbb{R}^2$. Däremot är det kanske ett nödvändigt vilkor? 

Ja!

Bara för att ha något att utgå från, så tänker jag att en cirkel väl alltid har hela $\mathbb{R}^2$ som omgång, vilket väl mer generellt även gäller för alla slutna och tillräckligt släta ($C^1$ borde väl räcka) kurvor? Så där har vi ett tillräckligt vilkor, men det är knappast nödvändigt, eftersom ju normalerna till en sluten slät kurva väl täcker hela $$\mathbb{R}^2 minst två gånger... 

C1 räcker tycker jag. Minst två gånger ja. Är cirkeln den enda kurvan som täcker R2 exakt två gånger?

Qetsiyah skrev:
Är cirkeln den enda kurvan som täcker R2 exakt två gånger?

Du ställer så många bra frågor! Du har en kul spinoff på ditt gymnasiearbete på gång här! ^_^

Dock får man vara lite försiktig med hur man uttrycker sig här, eftersom cirkelns centrum ju faktiskt täcks oändligt många gånger av cirkelns normaler.

Min första tanke var att ellipser kanske beter sig ungefär likadant som cirklar i det här avseendet, men nixpix, riktigt så enkelt är det inte. Kolla in den här bilden på normalerna till en ellips (tagen från Wolfram MathWorld):

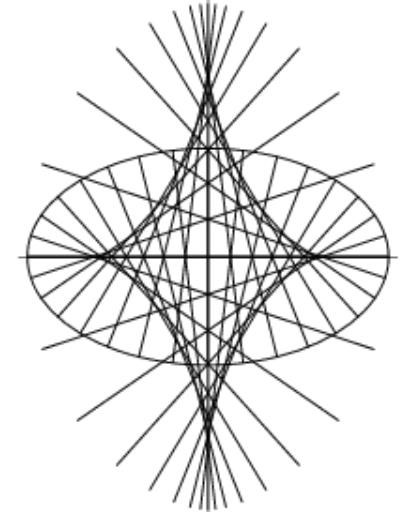
Nu när jag tänker efter så har jag faktiskt tidigare funderat på detta med just normalerna till ellipser (och mer generellt andra algebraiska kurvor som specificeras av polynomekvationer i två variabler). Det finns en metod inom datoralgebra som kallas för cylindrical algebraic decomposition (ingejörer brukar skina upp när jag säger att jag använder CAD, men bli ack så besvikna när jag förklarar närmare :D ), som i just det här fallet kan användas för att dela upp $\mathbb{R}^2$ i olika 'celler' beroende på hur många normaler som går igenom punkterna.

Min hjärna hoppar till något som liknar omloppstal. Om vi parametriserar kurvan med polära koordinater $r=r(t)$ och $\theta=\theta(t)$ för $0\leq t\leq1$ kan vi beräkna hur stor vinkel som kurvan vrider sig med hjälp av uttrycket $\theta(1)-\theta(0)$. Om $\theta(1)-\theta(0)\geq\pi$ borde väl omfånget bli $\mathbb{R}^2$?

Jag gillar idéen med att hålla koll på kurvans (eller kanske ännu hellre: tangentens?) vridning när vi går längs kurvan! Dock vet jag inte om polära koordinater är precis det som vi vill ha? (Men jag är öppen för att bli övertygad!)

Däremot vill jag minnas att vi till en slät kurva $\gamma: [0,L]\to \mathbb{R}^2$ (som för enkelhetens skull kan antas vara parametriserad "med båglängd" så att $\Vert{\gamma'(t)}\Vert=1$ för alla $t\in[0,L]$) kan associera en slät vinkelfunktion $\varphi:[0,1]\to\mathbb{R}$ sådan att

$\gamma'(t)=\begin{pmatrix}\cos(\varphi(t)),\sin(\varphi(t))\end{pmatrix}$ för alla $t\in [0,L]$.

Skulle det kunna vara så att omfånget för $\gamma$ garanterat blir hela $\mathbb{R}^2$ om $|\varphi(L)-\varphi(0)|\geqslant \pi$?

Påpekande: Notera att detta vilkor implicerar att det finns två punkter på kurvan som har parallella normaler (dvs. Qetsiyahs ursprungliga vilkor) men att att det är strikt starkare, eftersom det utesluter saker som linjesegment och kurvor i stil med denna:

Nepp, så enkelt är det inte. Efter en del funderande och ritande* tycker jag att jag har kommit fram till ett motexempel.

Idén är att formulera om den önskade egenakapen att omfånget för en plan kurva $\mathcal{C}\subset\mathbb{R}^2$ är hela $\mathbb{R}^2$ till följande ekvivalenta egenskap (som lite flummigt kan uttryckas som att "varje punkt kan använda kurvan som spegel"):

För varje punkt $\mathbf{p}\in\mathbb{R}^2$ så finns det en punkt $\mathbf{q}\in \mathcal{C}$, sådan att $\mathbf{p}-\mathbf{q}$ är parallell med normalen i $\mathbf{q}$ (eller ekvivalent: är vinkelrät mot tangentlinjen i $\mathbf{q}$).

Vi vill nu konstruera ett exempel på en kurva $\mathcal{C}$ som å ena sidan uppfyller AlvinB's eller mitt krav, men samtidigt är sådan att minst en punkt i $\mathbb{R}^2$ inte kan spegla sig i $\mathcal{C}$. Låt oss för enkelhetens skull säga att denna olycksaliga punkt ska vara origo.

Ett sätt att rent konkret åstadkomma detta är att därför rita utt (ett urval av) alla tänkbara räta linjer som går igenom origo, och försöker rita en kurva som aldrig skär någon av de linjerna med en rät vinkel (se några av kladdpapprena i bilden nedan). En stunds funderande (AlvinB's prat om polära koordinater hjälpte nog lite också) ger då att den spiralformade kurvan $\gamma:[\pi/2,5\pi/2]\to\mathbb{R}^2$ med

$\gamma(t)=(t\cos(t),t\sin(t))$

gör jobbet. En plot från Wolfram Alpha ser ut så här:

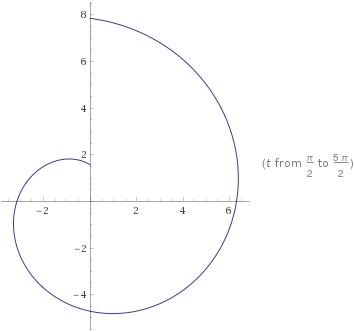
Det är enkelt att se att denna kurva uppfyller både mitt och AlvinB's kriterium (till exempel kan man genom att numeriskt undersöka $\gamma'(t)$ se att tangenten som vi får vid $t=\pi/2$ har hunnit vrida sig ett halvt varv redan vid $t\approx 1.39\pi$ och ett helt varv vid $t\approx 2.36\pi$), men likt förbannat så finns det inget $t\in[\pi/2,5\pi/2]$ som uppfyller att $\gamma(t)\perp \gamma'(t)$. (Detta kan man se rent visuellt, men det är en bra övning att övertyga sig om det algebraiskt också, genom att visa att $\gamma(t)\bullet \gamma'(t)\neq 0$ för alla $t\in [\pi/2,5\pi/2]$.)

Om inte jag har gjort något tankefel här ovan, så får vi nog reterera ytterligare från Qetsiyahs ursprungliga förmodan... Någon som har några idéer? Är vi helt övertygade om att en sluten slät kurva alltid har hela $\mathbb{R}^2$ som omfång? Annars är det kanske ett bra ställe att börja på? Det skulle också vara trevligt om man på något bra sätt kunde uttrycka vad den fundamentala skillnaden är mellan spiralen ovan och exempelvis en halvcirkel (som ju har hela $\mathbb{R}^2$ som omfång).

* De här kladdpapprena är misstänkt lika de "konstverk" som mina föräldrar har sparat från när jag gick på dagis...

Att normalerna kunde dansa runt ett område i mitten var något som jag inte tänkt på över huvud taget. Ritar man ut ett antal normaler syns ju ganska tydligt att vi får ett antal punkter i mitten som aldrig skärs av någon normal:

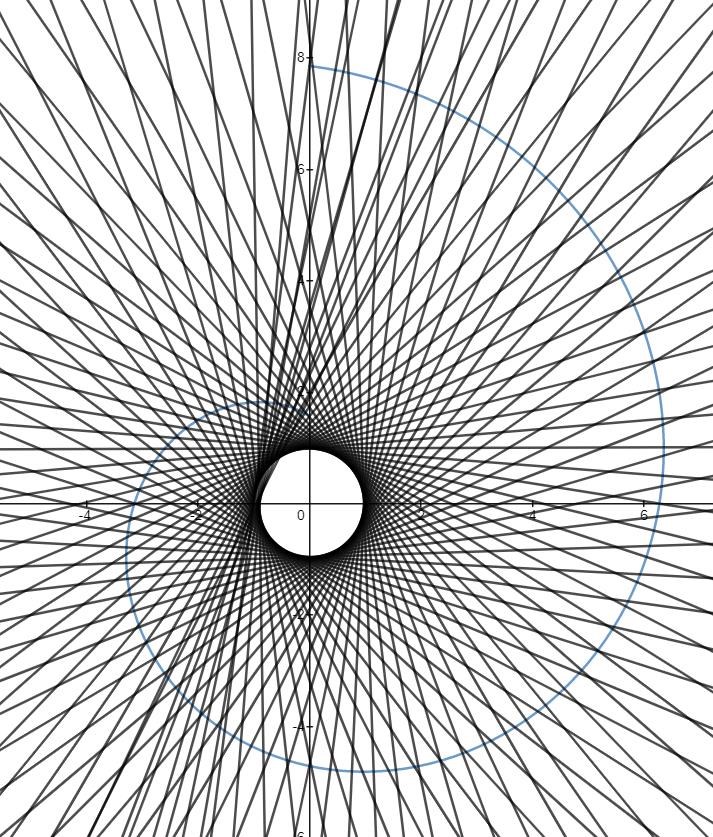
Rent spontant tycker jag det som möjliggör det här tomrummet i mitten är det faktum att avståndet till origo ökar. Hade det inte ökat borde vi inte kunna få något tomrum. Detta är väl en skillnad mot halvcirkeln, som har ett konstant avstånd till origo (om den är centrerad där).

Dock behöver grafer vars avstånd till origo ökar inte nödvändigtvis få sådana här tomrum i mitten. Om avståndet minskar igen tillräckligt mycket kan hålet täckas. Dock tycker jag vi bör kunna utesluta en kategori av kurvor, nämligen de för vilka avståndet till origo ökar eller minskar på hela kurvan (och där kurvan inte skär origo). Om $\gamma(t)=(x(t),y(t))$ innebär det ju att avståndet till origo ges av $\sqrt{x(t)^2+y(t)^2}$. Ett ökande avstånd till origo innebär då att:

$\dfrac{d}{dt}[x\left(t\right)^2+y\left(t\right)^2]>0$

$2x'(t)x(t)+2y'(t)y(t)>0$

$x'(t)x(t)+y'(t)y(t)>0$

$(x'(t),y'(t))\bullet(x(t),y(t))>0$

$\gamma'(t)\bullet\gamma(t)>0$

Detta innebär att kurvor vars avstånd till origo ökar längs hela kurvan omöjligen kan ha hela $\mathbb{R}^2$. Ett liknande resonemang kan göras för kurvor vars avstånd till origo minskar längs hela kurvan (vilket egentligen är samma sak, det beror ju bara på vilket håll man parametriserar kurvan).

Dessutom kan vi ju flytta koordinatsystemet så att vilken punkt som helst hamnar i origo. Detta borde betyda att kurvor vars avstånd till en viss punkt ökar längs hela kurvan (och som inte skär punkten) aldrig kan ha hela $\mathbb{R}^2$ som omfång.

(Observera att jag nu talar om att avståndet ökar i bemärkelsen att derivatan av avståndet är positiv. Avståndet kan ju vara växande, även om derivatan är noll i någon punkt.)

Jag hänger med midre desto längre ned i tråden jag läser, så jag kanske är ute och cyklar nu.

Denna spiral är väl inte en sluten kurva?

Jag är mer intresserad av varför denna spiral ger en tom enhetscirkel, det är mycket misstänkt.

Alvin: glömde du rottecknet när du skulle derivera avståndet?

AlvinB skrev:

Detta innebär att kurvor vars avstånd till origo ökar längs hela kurvan omöjligen kan ha hela $\mathbb{R}^2$. Ett liknande resonemang kan göras för kurvor vars avstånd till origo minskar längs hela kurvan (vilket egentligen är samma sak, det beror ju bara på vilket håll man parametriserar kurvan).

Dessutom kan vi ju flytta koordinatsystemet så att vilken punkt som helst hamnar i origo. Detta borde betyda att kurvor vars avstånd till en viss punkt ökar längs hela kurvan (och som inte skär punkten) aldrig kan ha hela $\mathbb{R}^2$ som omfång.

Men återigen så är det exemplet med halvcirkeln, om vi placerar den med start i origo så ökar dess avstånd från origo längs hela kurvan? 

Qetsiyah skrev:

Jag hänger med midre desto längre ned i tråden jag läser, så jag kanske är ute och cyklar nu.

Denna spiral är väl inte en sluten kurva?

Jag är mer intresserad av varför denna spiral ger en tom enhetscirkel, det är mycket misstänkt.

Nej, spiralen är inte en sluten kurva. Jag känner mig hyfsat säker på att slutna kurvor mycket riktigt har $\mathbb{R}^2$ som omfång.

Man kan undra vad det egentligen är för form i mitten. Det är egentligen inte en cirkel . Visst ser du att lite av cirkeln täcks där till vänster? Att hålet ser ut som det gör beror på vilka gränser vi har för $t$. Ovanstående bild har ju $\pi/2\leq t\leq 5\pi/2$. Tar vi istället $0\leq t\leq3\pi/2$

Jag har även ritat ut en grön halvcirkel för att illustrera att området i mitten inte är en halvcirkel. Tar vi istället $-\pi/2\leq t\leq\pi/2$ fås faktiskt en sluten kurva, som har hela $\mathbb{R}^2$ som omfång!

Alvin: glömde du rottecknet när du skulle derivera avståndet?

Ökar $\sqrt{x(t)^2+y(t)^2}$ ökar även $x(t)^2+y(t)^2$. Att derivera avståndet i kvadrat är enklare, så det är vanligt att man gör det istället.

Men återigen så är det exemplet med halvcirkeln, om vi placerar den med start i origo så ökar dess avstånd från origo längs hela kurvan?

Jo, men nu talade jag om kurvor vars avstånd till origo ökar på sådant sätt att derivatan är strikt större än noll. Detta är inte nödvändigtvis samma sak som att avståndet ökar. Se här.

Dessutom får ju kurvan inte skära origo, vilket den gör om halvcirkeln börjar i origo.

AlvinB skrev.

Nej, spiralen är inte en sluten kurva. Jag känner mig hyfsat säker på att slutna kurvor mycket riktigt har $\mathbb{R}^2$ som omfång.

Den måste vara deriverbar! En rektangel är sluten men har inte hela R2.

Man kan undra vad det egentligen är för form i mitten. Det är egentligen inte en cirkel . Visst ser du att lite av cirkeln täcks där till vänster?

Ja jag märkte det lite förtvivlat i efterhand... tråkigt

Ökar $\sqrt{x(t)^2+y(t)^2}$ ökar även $x(t)^2+y(t)^2$. Att derivera avståndet i kvadrat är enklare, så det är vanligt att man gör det istället.

Okej

Jo, men nu talade jag om kurvor vars avstånd till origo ökar på sådant sätt att derivatan är strikt större än noll. Detta är inte nödvändigtvis samma sak som att avståndet ökar. Se här.

Hmm okej men uppfyller inte en halvcirkel det?

På tal om allt detta undrar jag om det går att ha en enda punkt (ingen omgivning till den) som inte tillhör en kurvas omfång...

oggih skrev:

Däremot vill jag minnas att vi till en slät kurva $\gamma: [0,L]\to \mathbb{R}^2$ (som för enkelhetens skull kan antas vara parametriserad "med båglängd" så att $\Vert{\gamma'(t)}\Vert=1$ för alla $t\in[0,L]$)

Va?

kan associera en slät vinkelfunktion $\varphi:[0,1]\to\mathbb{R}$ sådan att

$\gamma'(t)=\begin{pmatrix}\cos(\varphi(t)),\sin(\varphi(t))\end{pmatrix}$ för alla $t\in [0,L]$.

?

Om $\gamma:[0,L]\to\mathbb{R}^2$ är en slät parametrisering av en kurva i planet, så kan vi tänka oss att $\gamma$ beskriver en partikels rörelse längs med kurvan, på ett sådant sätt att varje $t\in[0,L]$ anger en tidpunkt, och $\gamma(t)$ anger partikelns position vid tiden $t$.

Med detta synsätt så beskriver $\gamma'(t)$ partikelns hastighet vid tiden $t$ [denna kommer att vara parallell med kurvans tangentlinje i punkten $\gamma(t)$], nedan $\Vert \gamma'(t)\Vert$ beskriver partikelns fart.

Om $\Vert\gamma'(t)\Vert=1$ för alla $t\in[0,1]$ så betyder det att partikeln har den konstanta farten 1 längdenhet per tidsenhet under sin färd på kurvan. En sådan parametrisering går alltid att införa (det borde vara intuitivt klart att man alltid kan föreställa sig att en partikel rör sig med konstant fart längs kurvan), och detta är trevligt av två skäl:

Det ena skälet är att den totala sträckan som partikeln färdas från en viss tidpunkt $t_0$ till en annan tidpunkt $t_1$ helt enkelt blir $t_1-t_0$ längdenheter. Det är detta man menar när man kallar en sådan här parametrisering för en båglängdsparametrisering (parametrization by arclength på engelska).

Den andra trevliga konsekvensen är att derivatan vid varje punkt kommer vara en enhetsvektor i $\mathbb{R}^2$, och därmed kommer kunna skrivas på formen $(\cos(\varphi),\sin(\varphi))$ där $\varphi$ är en vinkel som anger derivatans riktning.

Notera att den här vinkeln är inte helt unikt bestämd, eftersom man alltid kan addera eller subtrahera en multipel av $2\pi$ utan att den motsvarande vektorn $(\cos(\varphi),\sin(\varphi))$ förändras. Om kurvan exempelvis är på väg rakt uppåt i en viss punkt, så att $\gamma'(t)=(0,1)$, så skulle vi t.ex. lika väl kunna säga att tangentvinkeln motsvarar $\varphi=\pi/2$ som att den motsvarar $\varphi=5\pi/2$. Däremot blir den unikt bestämd om vi kräver att $\varphi\in[0,2\pi)$.

Om vi vid varje tidpunkt $t\in[0,L]$ väljer en vinkel $\varphi\in\mathbb{R}$ sådan att $\gamma'(t)=(\cos(\varphi(t),\sin(\varphi(t))$, så får vi en vinkelfunktion $\varphi:[0,L]\to\mathbb{R}$. Återigen: eftersom vi vid varje tidpunkt kan slänga in hur många multiplar av $2\pi$ vi vill, så finns det oändligt många sätt att konstruera sådana här funktioner, och de flesta sådana valen ger fruktansvärt fula och diskontinuerliga funktioner.

So far so good hoppas jag. Det jag har beskrivt hittills är i någon mening självklarheter och innehåller inget matematiskt djup (men det kan så klart vara förvirrande ändå, så fråga om något är oklart!). Det intressanta kommer nu:

Om vi väljer $\varphi(0)\in[0,2\pi)$ så finns det ett unikt sätt välja $\varphi(t)\in\mathbb{R}$ för alla andra $t\in [0,L]$, sådant att $\varphi:[0,L]\to\mathbb{R}$ blir en slät funktion. (Notera att man då mycket väl kan bli tvungen att välja $\varphi(t)$ mindre än 0 eller mer än $2\pi$ för vissa $t$.)

Stanna gärna upp en stund och fundera över detta, och övertyga dig gärna om att det känns intuitivt rimligt! (Att ge ett formellt bevis är lite överkurs.) Rita t.ex. upp en kurva på ett papper, tillsammans med tangentlinjerna vid lite olika punkter, och fundera för vad denna unika släta vinkelfunktion blir i just det fallet.

Övningsuppgift: Kan du rita upp ett exempel på en kurva i planet där den här vinkelfunktionen kommer bli $3\pi$ vid någon tidpunkt? Kan du någon kurva där vinkelfunktionen blir $-\pi/2$ vid någon tidpunkt?

Bonusfakta: Ett av mina favoritresultat inom teorin för plana kurvor är Hopfs Umlaufsatz som säger följande:

Låt $\gamma:[0,L]\to\mathbb{R}^2$ vara en slät båglängdsparametrisering av kurva i planet, sådan att $\gamma(0)=\gamma(L)$ [dvs. kurvan är sluten] och $\gamma$ är injektiv på intervallet $(0,L)$ [dvs. kurvan är enkel], och låt $\varphi:[0,L]\to\mathbb{R}$ vara den unika släta vinkelfunktionen vars existens jag introducerade ovan. Då kommer $\varphi(L)-\varphi(0)$ antingen vara $2\pi$ eller $-2\pi$.

Försök gärna övertyga dig om att detta känns rimligt genom att rita upp lite exempel på enkla slutna släta kurvor (även detta är lite överkurs att bevisa formellt). 

Notera att det finns ett analogt (och betydligt mer lättbevisat) resultat i Euklidisk geometri, som säger att summan av yttervinklarna i en enkel polygon alltid blir $2\pi$.

Övninguppgift: Ge ett exempel som på en icke-enkel sluten slät kurva där $|\varphi(L)-\varphi(0)|\neq 2\pi$.

En bra och ganska lättillgänglig bok om man vill lära sig mer om släta kurvor, där både vinkelfunktionssatsen och Hopfs Umlaufsatz diskuteras, är Differential Geometry of Curves and Surfaces av Kristopher Tapp. Det borde räcka att ha linalg och flervariabelanalys (och möjligtvis en gnutta topologi) i bagaget för att komma igång med den!