Analysens huvudsats
Hej!
jag förstår inte helt denna uppgiften.
Uppgiften går ut på att derivera följande funktion. 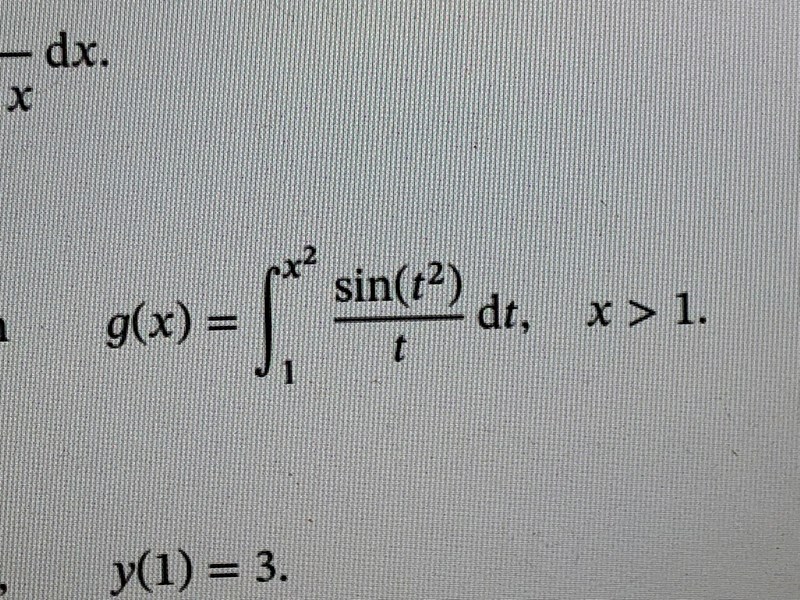
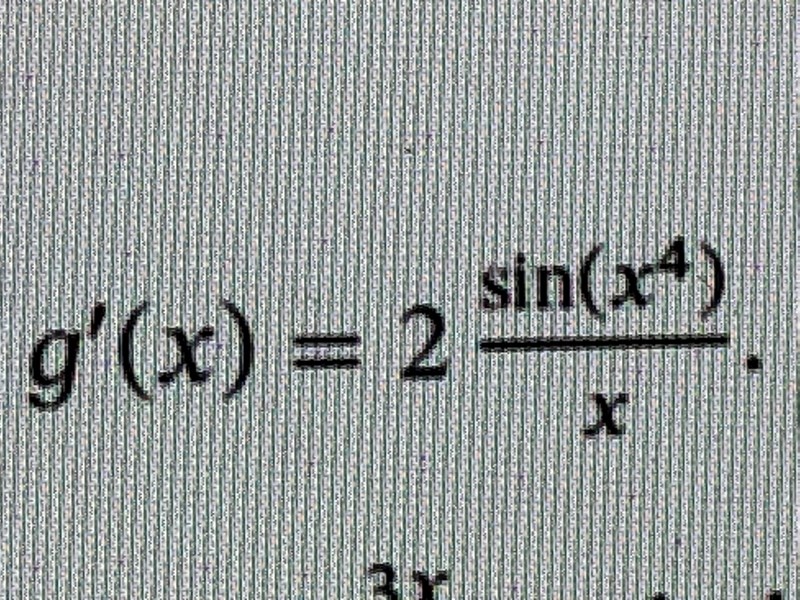
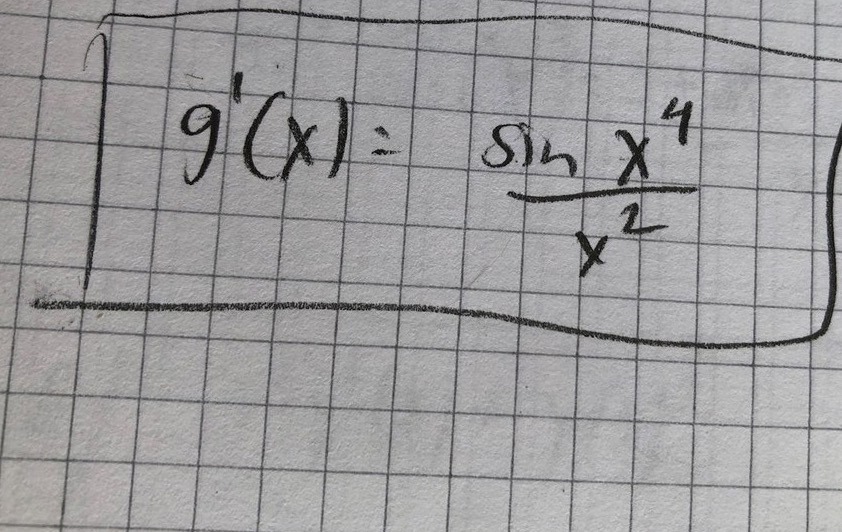

Ovan har jag bifogat rätt svar samt mitt svar. Jag har följt analysens huvudsats och "tagit bort integraltecknet samt stoppat in det övre värdet från integralen". Varför stämmer inte det? Har jag missförstått analysens huvudsats?
Om F(t) är en primitiv funktion till sin(t2)/t så är
g(x)=F(x2)-F(1)
Derivera och förenkla HL med kedjeregeln.
Tack för svar! Men När kan man då använda analysens huvudsats? Jag trodde det bara var att applicera satsen?
Och när jag ska beräkna derivatan av en integral använder jag väl huvudsatsen? Varför behöver jag först integrera sen derivera?
Detta är vad jag kommer fram till när jag stoppar in värdena.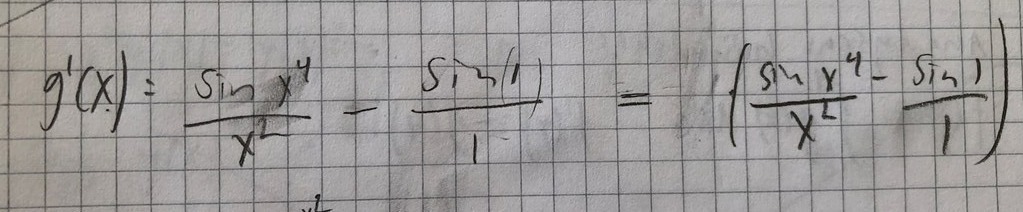
Grejen är den att du inte vet hur F(t) ser ut, men du vet att
F'(t)=sin(t2)t
Du vill räkna ut
g'(x)=F'(x2)·2x-0
(F(1) är en konstant.)
Ser du var kedjeregeln kommer in?
Dr. G skrev:Du vill räkna ut
g'(x)=F'(x2)·2x-0
(F(1) är en konstant.)
Varför vill jag räkna ut detta? Varför behöver jag derivera? Det känns som att jag har missförstått Analysens huvudsats. När jag kollar på satsen tycker jag att vi får:
F(x)=∫x21g(x) dx⇒F'(x)=g(x2)
Varför stämmer inte detta? Har det med en inre derivata på x2 att göra? Skulle mitt resonemang stämma om vi istället för x2hade x?
Aorta skrev:
Varför vill jag räkna ut detta? Varför behöver jag derivera?
Uppgiften var väl att ta fram g'(x)?
Det känns som att jag har missförstått Analysens huvudsats. När jag kollar på satsen tycker jag att vi får:
F(x)=∫x21g(x) dx⇒F'(x)=g(x2)
Varför stämmer inte detta?
Om G(t) är primitiv funktion till g(t) så blir integralen G(x2) - G(1), eller hur?
Om du deriverar m.a.p x så finns en inre derivata. F'(x) = G'(x2)*2x = g(x2)*2x.
Har det med en inre derivata på x2 att göra? Skulle mitt resonemang stämma om vi istället för x2hade x?
Ja, precis. Då skulle integralen bli G(x) - G(1) och derivatan av integralen m.a.p x blir G'(x) = g(x).
Tack för hjälpen! Jag behövde låta dte marinera ett tag men nu är jag med!


