Andra koordinatsystem

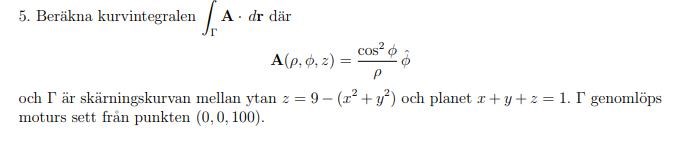
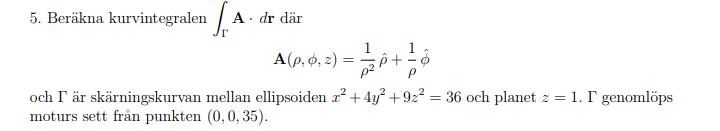
Gör en tråd för varje fråga du behöver hjälp med. Visa för varje fråga hur du har försökt och hur långt7 du har kommit /moderator

Smaragdalena skrev:

Gör en tråd för varje fråga du behöver hjälp med. Visa för varje fråga hur du har försökt och hur långt7 du har kommit /moderator

 Läste du ens vad frågan var? Jag kommer ju ingenstans!

Om vi börjar med den översta:

Du måste antingen omvandla vektorfältet från cylindriska koordinater till kartesiska koordinater, eller ta fram kurvan i cylindriska koordinater. Båda funkar lika bra, det handlar nog mest om vad du känner dig mest bekväm med.

Om du inte har alla samband mellan koordinatsystemen i huvudet kan du använda dig av dessa tabeller:

https://en.wikipedia.org/wiki/Del_in_cylindrical_and_spherical_coordinates

När du väl har vektorfältet och kurvan i samma koordinatsystem finner du att vektorfältet är konservativt (rotationen är lika med nollvektorn), vilket lätt ger svaret med hjälp av Stokes sats.

EDIT: Eller om du kan konstatera att fältet är konservativt behöver du egentligen inte veta mer om kurvan än att den är sluten för att säga att integralen blir noll enligt Stokes sats men du kan inte veta att fältet är konservativt på förhand, så jag skulle nog ändå säga att båda tillvägagångssätten är likvärdiga.

Är det här en början, eller är jag helt ute och cyklar nu?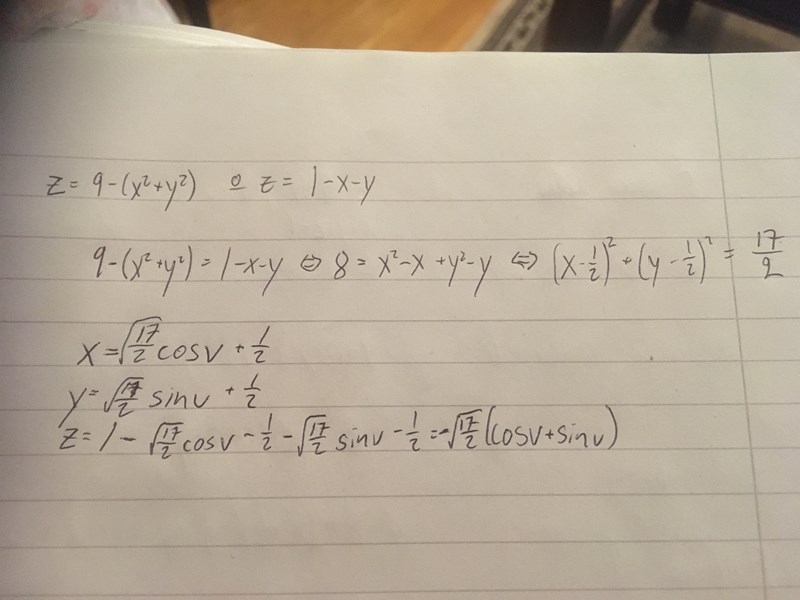

Nu hänger jag inte riktigt med på vad du försöker göra. För enkelhetens skull kör jag nu på varianten att konvertera vektorfältet till kartesiska koordinater.

Vi har vektorfältet:

$\mathbf{A}(\rho,\phi,z)=$ $\dfrac{\cos^2(\phi)}{\rho}\hat{\mathbf{\phi}}$

och vi vill uttrycka detta i det kartesiska koordinatsystemet. Vi vet följande samband:

$\rho^2=x^2+y^2$

$x=\rho\cos(\phi)$

$y=\rho\sin(\phi)$

$z=z$

Från tabellen jag länkade ser vi även att enhetsvektorn $\hat{\mathbf{\phi}}$ i kartesiska koordinater är lika med:

$\hat{\mathbf{\phi}}=$ $\dfrac{-y\hat{\mathbf{x}}+x\hat{\mathbf{y}}}{\sqrt{x^2+y^2}}$

Använd detta för att omvandla vektorfältet till kartesiska koordinater. Sedan är det bara att göra som med vilken kurvintegraluppgift med Stokes sats som helst. Dock får vi det väldigt lätt för oss eftersom fältet är konservativt.

Hur/varför är rotationen 0? 

Micimacko skrev:

Hur/varför är rotationen 0? 

 När du fått fram $\mathbf{A}$ i kartesiska koordinater kan du beräkna $\nabla\times\mathbf{A}$ och så ser du att rotationen blir noll. Då är det med hjälp av Stokes sats lätt att se att kurvintegralen blir noll.

Blev det rätt nu då?

Japp, det stämmer!

Ser du nu att $\nabla\times\mathbf{A}=0$?

Hänger du med på att detta tillsammans med Stokes sats ger att kurvintegralen blir lika med noll?

Jag får det inte till 0 🙈 Vad har jag ställt till med nu?

Du har nog räknat fel någonstans. Det är nämligen så att:

$\dfrac{\partial Q}{\partial x}=\dfrac{\partial}{\partial x}[\dfrac{x^3}{(x^2+y^2)^2}]=\dfrac{3x^2y^2-x^4}{(x^2+y^2)^3}$

$\dfrac{\partial P}{\partial y}=\dfrac{\partial}{\partial y}[-\dfrac{x^2y}{(x^2+y^2)^2}]=\dfrac{3x^2y^2-x^4}{(x^2+y^2)^3}$

Det gäller alltså att:

$\dfrac{\partial Q}{\partial x}=\dfrac{\partial P}{\partial y}$

vilket gör att även $z$-komponenten i $\nabla\times\mathbf{A}$ blir noll.

Jag får helt olika :( 

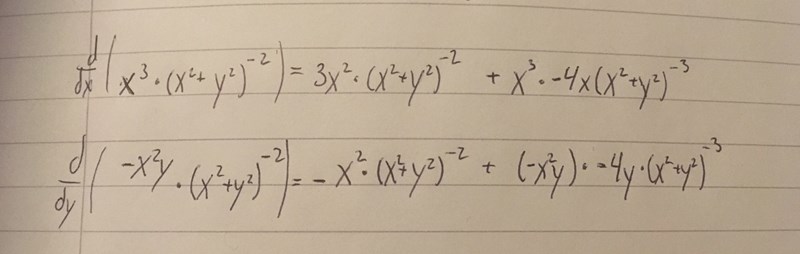
Skriv bråken med gemensam nämnare så får du samma svar som jag:

$3x^2\cdot(x^2+y^2)^{-2}+x^3\cdot-4x(x^2+y^2)^{-3}=$ $=\dfrac{3x^2}{(x^2+y^2)^2}-\dfrac{4x^4}{(x^2+y^2)^3}=\dfrac{3x^2(x^2+y^2)}{(x^2+y^2)^2(x^2+y^2)}-\dfrac{4x^4}{(x^2+y^2)^3}=$

$=\dfrac{3x^4+3x^2y^2}{(x^2+y^2)^3}-\dfrac{4x^4}{(x^2+y^2)^3}=\dfrac{3x^4+3x^2y^2-4x^4}{(x^2+y^2)^3}=\dfrac{3x^2y^2-x^4}{(x^2+y^2)^3}$

och den andra:

$-x^2\cdot(x^2+y^2)^{-2}+(-x^2y)\cdot-4y(x^2+y^2)^{-3}=$ $=\dfrac{-x^2}{(x^2+y^2)^2}+\dfrac{4x^2y^2}{(x^2+y^2)^3}=\dfrac{-x^2(x^2+y^2)}{(x^2+y^2)^2(x^2+y^2)}+\dfrac{4x^2y^2}{(x^2+y^2)^3}=$

$=\dfrac{-x^4-x^2y^2}{(x^2+y^2)^3}+\dfrac{4x^2y^2}{(x^2+y^2)^3}=\dfrac{-x^4-x^2y^2+4x^2y^2}{(x^2+y^2)^3}=\dfrac{3x^2y^2-x^4}{(x^2+y^2)^3}$

Tack!

Nej, nu har ni landat lite fel i tråden.

Vektorfältet $\mathbf{A}$ är singulärt på z-axeln $x^2+y^2=0$. Utanför z-axeln är det kontinuerligt deriverbart. Eftersom $\nabla \times \mathbf{A}=0$ kan Stoke's sats medföra förenklade beräkningar.

Men då måste man observera att z-axeln, där fältet är singulärt, ej får skära den yta, på vilken man tillämpar Stoke's sats.

Uppgiften blir därmed att hitta en sätt att gå runt singulariteten och samtidigt få en så enkel integral som möjligt.

Guggle skrev:

Nej, nu har ni landat lite fel i tråden.

Vektorfältet $\mathbf{A}$ är singulärt på z-axeln $x^2+y^2=0$. Utanför z-axeln är det kontinuerligt deriverbart. Eftersom $\nabla \times \mathbf{A}=0$ kan Stoke's sats medföra förenklade beräkningar.

Men då måste man observera att z-axeln, där fältet är singulärt, ej får skära den yta, på vilken man tillämpar Stoke's sats.

Uppgiften blir därmed att hitta en sätt att gå runt singulariteten och samtidigt få en så enkel integral som möjligt.

 Fasen att jag inte tänkte på det. Tur att det är någon som har ordning på torpet. :-)

EDIT: Förresten, jag får passa på att fråga. Är det över huvud taget värt att försöka använda Stokes sats i och med att man ändå måste beräkna den inre kurvans integral, eller ska man bara direkt försöka sig på en parametrisering?

Okej. Jag prövade mig på att parametrisera kurvan. Inte skoj. Det är nog ett mycket klokare drag att använda Stokes sats på något vis. Eftersom $\nabla\times\mathbf{A}=0$ kan vi välja i princip vilken mittenkurva som helst (så länge den går runt $z$-axeln) och ändå veta att den sammanlagda kurvintegralen av den yttre och inre kurvan (notera att den inre genomlöps i motsatt riktning) blir noll.

En relativt enkel inre kurva blir skärningen mellan planet och cylindern $x^2+y^2=1$:

Eftersom man vet att integralen för både den inre och den yttre tillsammans blir noll kan man sätt ett värde på den yttre kurvintegralen genom att bara beräkna den inre kurvans integral (vilket är betydligt enklare).

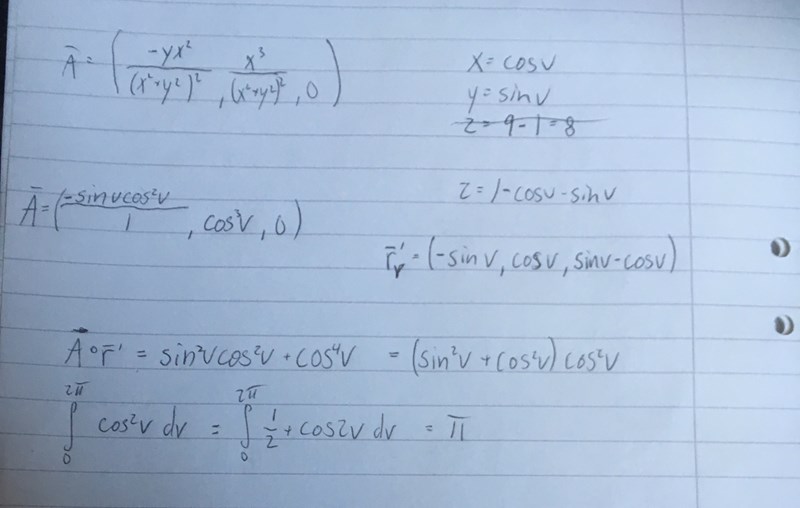Sådär va?

Nästan där. Med Stokes sats genomlöps faktiskt den inre kurvan i negativ (medurs) riktning. Detta gör att du får ett minustecken på svaret, d.v.s. $-\pi$.

Om man undrar varför detta är fallet kan det hjälpa att dela upp området i två:

Kurvintegralerna av de raka linjerna tar ut varandra och man blir kvar med att den yttre kurvan blir positivt orienterad och den inre blir negativt orienterad.

Blir det minus i svaret då? Eller blir det hela minus bit 1 = bit 2, alltså 0- -pi = pi?

Hela integralen blir negativ eftersom vi genomlöper den åt andra hållet. Svaret blir alltså $-\pi$.

Helsike vad jag svamlar. Kurvintegralen för den inre kurvan blir negativ, men minustecknen tar ut varandra då $\Gamma$-kurvans integral är lika med minus den inre kurvans integral.

EDIT: För att sammanfatta:

Vektorfältet $\mathbf{A}$ blir i kartesiska koordinater:

$\mathbf{A}(x,y,z)=$ $(\dfrac{-yx^2}{(x^2+y^2)^2},\dfrac{x^3}{(x^2+y^2)^2},0)$

Därefter använder vi oss av Stokes sats. Rotationen av vektorfältet är $\nabla\times\mathbf{A}=0$, men det finns en singularitet längs $z$-axeln. Därför går vi runt den med en kurva $C$ som genomlöps i medurs riktning. Vi väljer denna kurva till att vara skärningskurvan mellan planet och cylindern $x^2+y^2=1$ eftersom vi då får en lättberäknelig integral. Stokes sats ger att:

$\displaystyle\int_{\Gamma+C}\mathbf{A}\cdot d\mathbf{r}=0$

Detta kan vi omvandla till:

$\displaystyle\int_{\Gamma}\mathbf{A}\cdot d\mathbf{r}=-\int_{C} \mathbf{A}\cdot d\mathbf{r}$

Kurvintegralen av $C$ kan relativt enkelt beräknas med en parametrisering. Eftersom kurvan genomlöps medurs får man ett minustecken framför

$\displaystyle\int_C\mathbf{A}\cdot d\mathbf{r}=-\int_0^{2\pi}...\ dv=-\pi$

Den sökta integralen blir då detta med omvänt tecken:

$\displaystyle\int_{\Gamma}\mathbf{A}\cdot d\mathbf{r}=\pi$

Edit: Nu hann visst Alvin rätta sig medan jag skrev inlägget, men låter mitt inlägg stå kvar eftersom det innehåller så mycket vackra integraler!

Nja, rätt resonerat Alvin, men du slarvade förmodligen med uppställningen av Stokes sats. Rätt svar är $+\pi$, så här

$\displaystyle \oint_C \mathbf{A} \cdot d\mathbf{r}=\int_S(\nabla \times \mathbf{A})\cdot d\mathbf{S}$

Dela upp i en tvåsidig yta, låt $C_1$ vara kurvan till integralen vi söker, låt $C_2$ vara en kurva som omsluter z-axeln i motsatt riktning, dvs medurs

$\displaystyle \oint_{C_1} \mathbf{A} \cdot d\mathbf{r}+\oint_{C_2} \mathbf{A} \cdot d\mathbf{r}=0$

$\displaystyle \oint_{C_1} \mathbf{A} \cdot d\mathbf{r}=-\oint_{C_2} \mathbf{A} \cdot d\mathbf{r}$

Om vi nu byter genomloppsriktning på $C_2$, dvs genomlöper kurvan moturs så byter integralen tecken

$\displaystyle \oint_{C_1} \mathbf{A} \cdot d\mathbf{r}=\oint_{-C_2} \mathbf{A} \cdot d\mathbf{r}$

Vi parametriserar en cirkel runt z-axeln i xy-planet med radien $\rho$, vi lämnar $\rho, \alpha$ oförändrad i planet så det är enkelt att använda fältet $\mathbf{A}(\mathbf{r}(u))$

$\displaystyle \mathbf{r}(\alpha)=\rho\hat{\rho}+(1-\rho(\cos(\alpha)+\sin(\alpha))\hat{z}$

$\displaystyle \frac{d\mathbf{r}(\alpha)}{d\alpha}=\rho\hat{\alpha}+\rho(\sin(\alpha)-\cos(\alpha))\hat{z}$

$\displaystyle \oint_{-C_2} \mathbf{A} \cdot d\mathbf{r}=\int_0^{2\pi} \frac{\cos^2(\alpha)}{\rho}\hat{\alpha}\cdot \displaystyle \frac{d\mathbf{r}(\alpha)}{d\alpha}\,d\alpha=\int_0^{2\pi} \cos^2(\alpha)\,d\alpha=\pi$

Guggle skrev:

Nja, rätt resonerat Alvin, men du slarvade förmodligen med uppställningen av Stokes sats. Rätt svar är $+\pi$, så här

[...]

 Jo, jag märkte det.

Man kanske inte borde syssla med flervariabelanalys efter en natt med fem timmars sömn...