Andragradekvation problem

Är frågan $\sqrt{6x}+1 -\sqrt{2x+1}+2=0$? Lite rörigt ba

magmyr01 skrev:

Hej alla!

 

Jag försöker lösa en andragradsekvation men får inte rätt svar.

Här är länken till problemet och hur jag försökte lösa det.

https://imgur.com/a/wWu7Q0C

På radet 8 fick jag:

$6x + 1 = (-x-1{)}^2$

Enligt 1a kvadreringsregeln skulle H.L. bli såhär:

$(-x{)}^2-2*(-x)*(-1)+1$

men rätt lösning är

$(-x{)}^2-2*(-x)+1$

 

Det som jag inte förstår är var är (-1) där? 

Vad är det som jag gör fel?

 

Tack i förväg!

Hej och välkommen till Pluggakuten!

Jag trodde att du försökte använda 2:a kvadreringsregeln $(a-b)^2=a^2-2ab+b^2$.

I så fall är $a=-x$ och $b=1$ och du skulle då få $(-x-1)^2=(-x)^2-2\cdot (-x)\cdot 1+1^2$. Jag har markerat var det då blev fel nedan.

--------

(För att minska risken för slarvfel så kan du först bryta ut (-1) ur högerledet innan du kvadrerar.

Då blir uttrycket istället $((-1)(x+1))^2=(-1)^2(x+1)^2$)

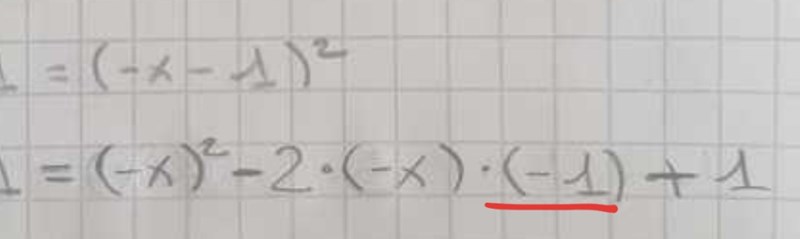
Men om du istället vill använda 1:a kvadreringsregeln $(a+b)^2=a^2+2ab+b^2$ så är $a=-x$ och $b=-1$.

Då blir $(-x-1)^2=(-x)^2+2(-x)(-1)+(-1)^2$.

La in din bild direkt i inlägget, för att underlätta för dem som vill svara.  Så här gör du för att lägga in bilden själv. /moderator

TETEK skrev:

Är frågan $\sqrt{6x}+1 -\sqrt{2x+1}+2=0$? Lite rörigt ba

Jap. Nu ser jag att det ser lite oklart i första radet!

Yngve skrev:

magmyr01 skrev:

Hej alla!

 

Jag försöker lösa en andragradsekvation men får inte rätt svar.

Här är länken till problemet och hur jag försökte lösa det.

https://imgur.com/a/wWu7Q0C

På radet 8 fick jag:

$6x + 1 = (-x-1{)}^2$

Enligt 1a kvadreringsregeln skulle H.L. bli såhär:

$(-x{)}^2-2*(-x)*(-1)+1$

men rätt lösning är

$(-x{)}^2-2*(-x)+1$

 

Det som jag inte förstår är var är (-1) där? 

Vad är det som jag gör fel?

 

Tack i förväg!

Hej och välkommen till Pluggakuten!

Jag trodde att du försökte använda 2:a kvadreringsregeln $(a-b)^2=a^2-2ab+b^2$.

I så fall är $a=-x$ och $b=1$ och du skulle då få $(-x-1)^2=(-x)^2-2\cdot (-x)\cdot 1+1^2$. Jag har markerat var det då blev fel nedan.

--------

(För att minska risken för slarvfel så kan du först bryta ut (-1) ur högerledet innan du kvadrerar.

Då blir uttrycket istället $((-1)(x+1))^2=(-1)^2(x+1)^2$)

Ja! Jag skrev det fel. Så det betyder att när man skriver om ekvationen ska man inte ta med +/- tecken utan att man bara skriver om nummer utan tecken och kopierar formeln, som t.ex. här skulle det vara $a^2 + 2ab + b^2$. Så att -1 i problemet skrivs om som 1?

Hoppas att jag förklarade mig på rätt sätt!

Edit: Jag ser att du skrev 1, så att 1 tappar minus tecknet, men -x fortfarande behåller minus tecknet. Är det någonting jag inte ser?

Smaragdalena skrev:

La in din bild direkt i inlägget, för att underlätta för dem som vill svara.  Så här gör du för att lägga in bilden själv. /moderator

Jag försökte ladda upp bilden direkt i sidan men jag fick ett fel och då tänkte jag att såhär skulle bli okej. Jag försöker igen för nästa gången.

magmyr01 skrev:

Ja! Jag skrev det fel. Så det betyder att när man skriver om ekvationen ska man inte ta med +/- tecken utan att man bara skriver om nummer utan tecken och kopierar formeln, som t.ex. här skulle det vara $a^2 + 2ab + b^2$. Så att -1 i problemet skrivs om som 1?

 

Hoppas att jag förklarade mig på rätt sätt!

 

Edit: Jag ser att du skrev 1, så att 1 tappar minus tecknet, men -x fortfarande behåller minus tecknet. Är det någonting jag inte ser?

Du vill utveckla kvadraten $(-x-1)^2$ med hjälp av någon av kvadreringsreglerna.

Första kvadreringsregeln lyder $(a+b)^2=a^2+2ab+b^2$, dvs det är ett plustecken mellan de två termerna inom parentesen.

Om du vill använda första kvadreringsregeln underlättar det därför om du skriver om ditt uttryck så att det är ett plustecken mellan termerna: $(-x-1)^2=((-x)+(-1))^2$. Om du jämför detta med "mallen" $(a+b)^2$ så ser du att $a$ motsvaras av $-x$ och att $b$ motsvaras av $-1$.

Då blir alltså utvecklingen $(-x)^2+2\cdot (-x)\cdot (-1)+(-1)^2=x^2+2x+1$

-----------------------------

Andra kvadreringsregeln lyder $(a-b)^2=a^2-2ab+b^2$, dvs det är ett minustecken mellan de två termerna inom parentesen.

Eftersom du redan har ett minustecken mellan termerna i ditt uttryck så kan du använda den regeln direkt.

Ditt uttryck är $((-x)-(1))^2$. Om du jämför detta med "mallen" $(a-b)^2$ så ser du att $a$ motsvaras av $-x$ och att $b$ motsvaras av $1$.

Då blir alltså utvecklingen $(-x)^2-2\cdot (-x)\cdot 1+(-1)^2=x^2+2x+1$

-----------------------------

Samma resultat, som sig bör.

------------------------------

Men det enklaste är nog att bryta ut -1 ur parentesen innan du använder kvadreringsregeln, som jag nämnde tidigare.