Andragradsekvation matte2b
Hej! Hade behövt hjälp med denna så snart som möjligt! Tack på förhand
Gissar ni håller med derivata, annars blir det klurigt.
Om basen på rektangeln är x, vad är då höjden (uttryckt i x)?
Med basen och höjden kan du skapa en funktion A(x). Det är extrempunkten (maxvärdet) till den du söker, i rätt intervall.
Kommer du vidare?
sictransit skrev:Gissar ni håller med derivata, annars blir det klurigt.
Om basen på rektangeln är x, vad är då höjden (uttryckt i x)?
Med basen och höjden kan du skapa en funktion A(x). Det är extrempunkten (maxvärdet) till den du söker, i rätt intervall.
Kommer du vidare?
Nej derivata har jag inte hört innan, såhär står det i facit iaf om det hjälper
Mitt fel! Jag tänkte lite för avancerat.
Om basen på rektangeln är x, så säger uppgiften att höjden (alltså y) är 5-2x.
Arean för en rektangel är ju basen * höjden, så vi kan sätta upp ett uttryck för den: A=x(5-2x). Så här ser den ut:
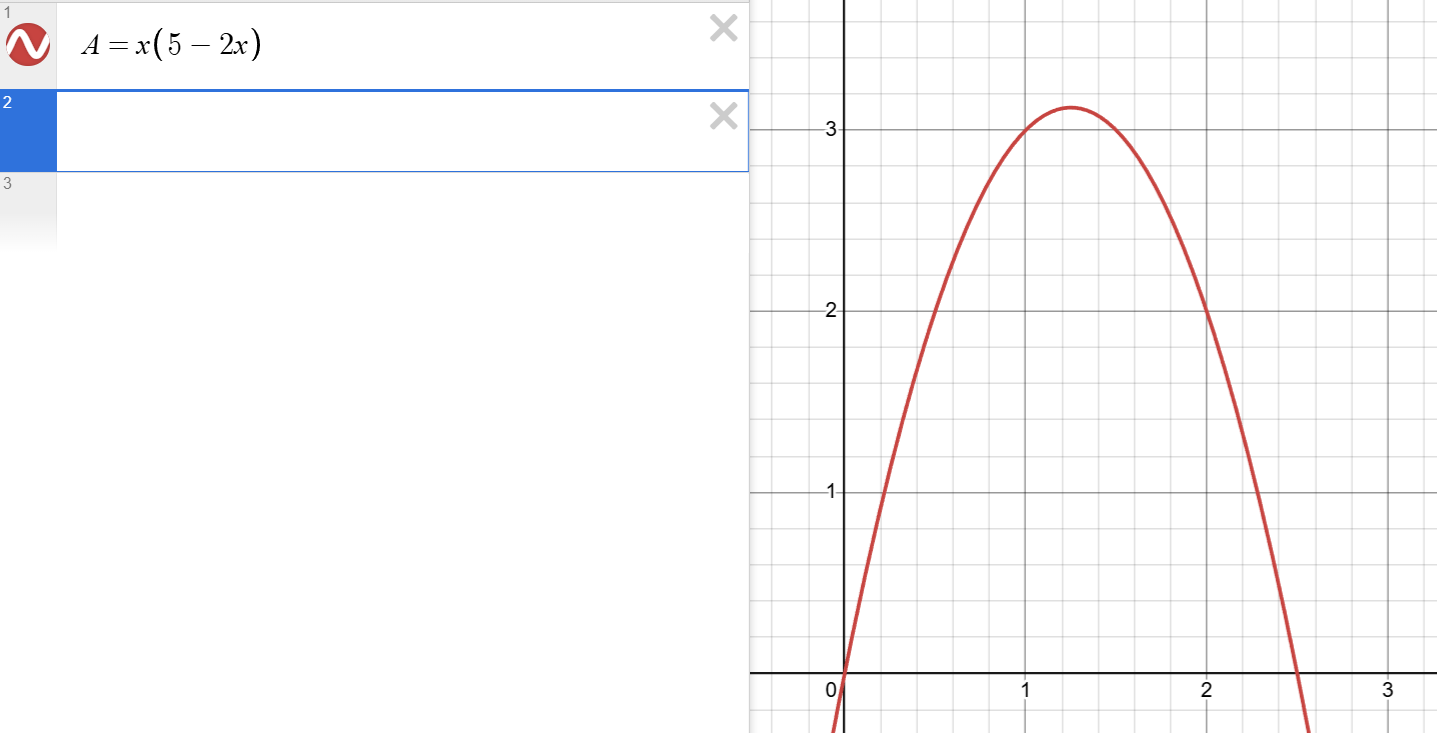
Som du ser har den ett maxvärde någonstans mellan x=1 och x=2.
Man kan hitta det med "derivata" som jag nämnde, men det finns andra sätt också.
Om vi kan hitta när den där röda kurvan skär x-axeln så ligger maxpunkten mitt emellan, på det som kallas symmetrilinjen.
Vi behöver alltså lösa den här ekvationen: x(5-2x)=0
Hängde du med så här långt?
Visa spoiler
Symmetrilinjen är i pq-formlen.
Man ser i figuren att rektangelns area är noll för x=0 och x=2,5.
Maxarean ges av x mitt emellan dessa värden.
(Areafunktionens symmetrilinje ligger mitt emellan dess nollställen.)
