Ang sannolikhetslära

Är det a) eller b) som ska vara 0,028? :)

   Det är b) uppgift tack 

Okej, först en fråga: Vilken sannolikhetsfunktion har binomialfördelningen i uppgiften? :)

charlie2016 skrev:

   Det är b) uppgift tack 

Visa spoiler

Det är b) uppgift tack 🙏🏽🙏🏽

Du har angivit rätt fördelning:        Bin(n, p),  där  n=100  och  p=1/365

och rätt sannolikhetsfunktion:      P(ksi = k) = [n över k] · (p^k) · (1 - p)^(n-k)

Det frågas efter        P(ksi = 2)  =   [n över 2] · (p^2) · (1 - p)^98    

Sätt in  n=100  och  p=1/365  och räkna ut.

Det ser ut som du var på rätt väg (kanske) men du kan ju aldrig någonsin stoppa in ett närmevärde med en enda ynklig liten signifikant siffra och hoppas få ett svar med 2 signifikanta siffror.  Det räcker inte med två heller när de ska manglas i hundra operationer!

Generellt gäller att vänta så länge det bara är möjligt att använda närmevärden.

jag gjorde fel med min Avrundning men fick rätt till slut på 1/365 = 0,00274 men väldig märklig jag får fortfarande inte 0,028 jag får istället 0,9972717 istället 🤔🤔

Vilken sannolikhetsfunktion har binomialfördelningen i uppgiften? :)

På uppgift b) står En annan grupp av 100 personer . Bestäm sannolikheten att exakt 2 av dem är födda den 1 januari.

min värde är rätta men jag får inte 0,028 

tack 🙏🏽🙏🏽🙏🏽

Se mitt förra inlägg:

Du har angivit rätt fördelning:        Bin(n, p),  där  n=100  och  p=1/365

och rätt sannolikhetsfunktion:      P(ksi = k) = [n över k] · (p^k) · (1 - p)^(n-k)

Det frågas efter        P(ksi = 2)  =   [n över 2] · (p^2) · (1 - p)^98    

                                    Sätt in  n=100  och  p=1/365  och räkna ut.

Här är ett närmevärde på  1/365 med  7 värdesiffror: 0.002739726  

Visa vilka siffervärden du använder i formeln.

På'n igen!

charlie2016 skrev:

På uppgift b) står En annan grupp av 100 personer . Bestäm sannolikheten att exakt 2 av dem är födda den 1 januari.

min värde är rätta men jag får inte 0,028 

tack 🙏🏽🙏🏽🙏🏽

Vi kommer till problemet med din lösning om du bara svarar på frågan; Vilken sannolikhetsfunktion har denna binomialfördelning? 

Svara på den frågan först, så kommer felet i din lösning att framgå snart. :)

Råkade jag skriva med osynligt bläck?   :-)

oj jag ber så mycket om ursäkt jag skulle bestämma sannolikhet med 2 

tack så mycket 

väldig nöjd med denna hjälp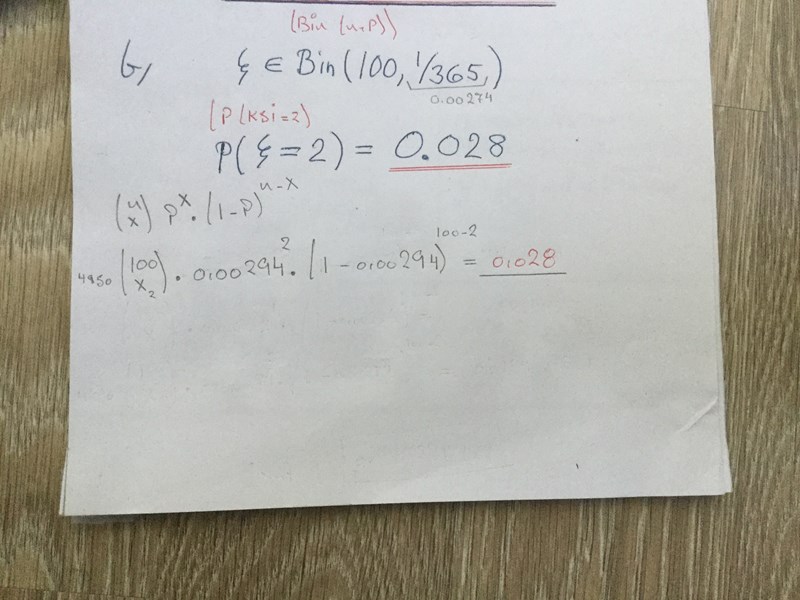

Vad betyder  x₂  i första faktorn? 
Den måste ju också få ett siffervärde.

Nej det är inte X2 jag skrev för bara egen bruk det skall vara en 2 där eller X 

Det måste vara ett siffervärde. Se formeln för  P(ksi = 2).

En sak till, varifrån kommer p-värdet  0,00294 ?

charlie2016 skrev:

oj jag ber så mycket om ursäkt jag skulle bestämma sannolikhet med 2 

Du behöver inte be om ursäkt, du behöver bara svara på frågan. Vi ställer frågor för att hjälpa dig komma fram till svaret på din fråga, så att du nästa gång ska kunna lösa uppgiften själv. Meningen med Pluggakuten är inte att du ska få lösningar serverade, utan att du ska få hjälp att lösa uppgiften själv.

Eftersom du nu är nöjd med hjälpen är tråden utagerad, men jag vill ändå understryka att du fortfarande inte har svarat på frågan jag nu har ställt tre gånger: Vilken sannolikhetsfunktion har binomialfunktionen i uppgiften? 

Oj jag glömde och svara på din fråga 🙏🏽🙏🏽Det va inte med meningen 🙏🏽🙏🏽🙏🏽sannolikheten är 2 på uppgift b) 

Sannolikhetsfunktionen är inte 2. Vad är en sannolikhetsfunktion? :)

Korrekt! I din lösning i trådstarten, vad har du beräknat? :)