Ange ekvationens största lösning i intervallet

Så långt har jag kommit med uppgift 27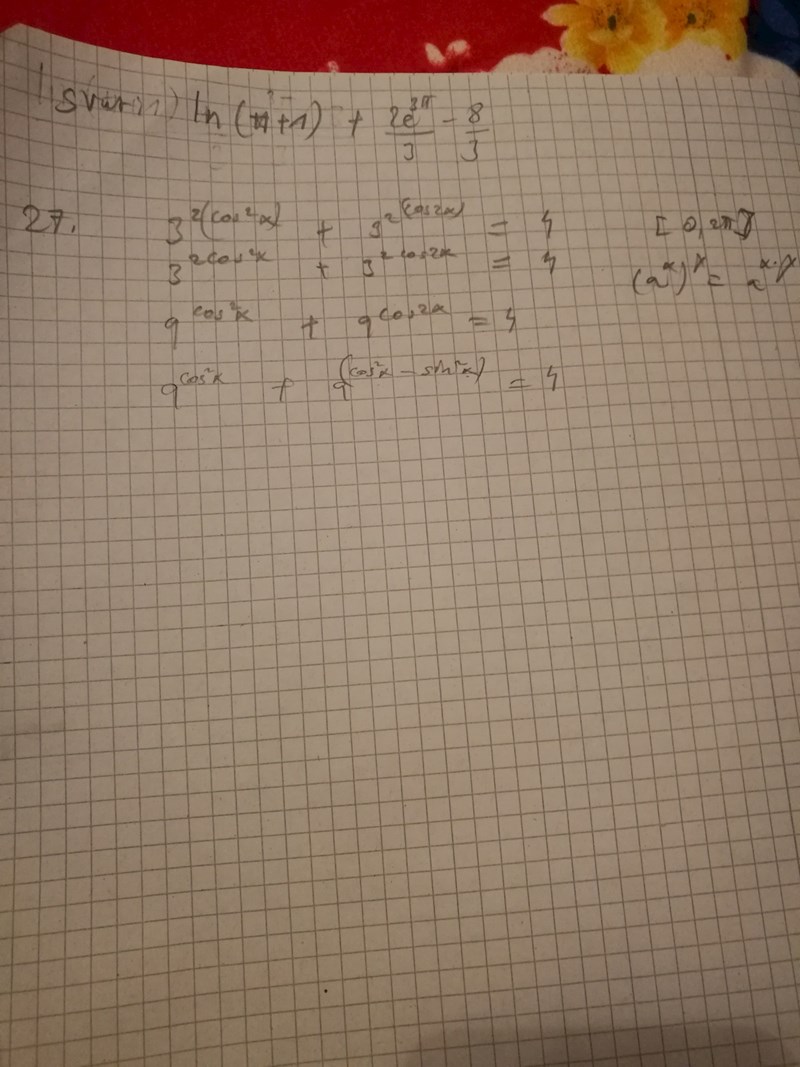 

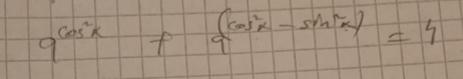
Trigonometriska 1:an: ${\cos }^{2}x + {\sin }^{2}x = 1$ger ${\sin }^{2}x = 1-{\cos }^{2}x$
flytta över 4 också

$9^{{\cos }^{2}x} + 9^{({\cos }^{2}x-(1-{\cos }^{2}x\left)\right)}-4 = 0$

$9^{{\cos }^{2}x} + 9^{(2{\cos }^{2}x-1)} - 4 = 0$

$9^{-1} = \frac{1}{9}$

$9^{{\cos }^{2}x} + 9^{2{\cos }^{2}x}*\frac{1}{9} - 4 = 0$

Potensregel: $a^{xy} = {\left(a^x\right)}^y, där y=2 och x={\cos }^{2}x$

$9^{{\cos }^{2}x} + 9^{{\left({\cos }^{2}x\right)}^2} *\frac{1}{9}-4 = 0$

Ersätt t = $9^{{\cos }^{2}x}$

t + $t^2 * \frac{1}{9} - 4$= 0

ger t = -12 och t = 3

t = -12 inte giltig eftersom $9^{{\cos }^{2}x} inte kan vara negativ$

t=3: 3 = $9^{{\cos }^{2}x}$

Skriv om $9^{{\cos }^{2}x} till basen 3: 3^{2{\cos }^{2}x}$

$9^{{\cos }^{2}x} = 3^1 (t-värdet 3)$

ger att $2{\cos }^{2}x = 1$

${\cos }^{2}x = \frac{1}{2}$

cos x = $\pm \frac{1}{\sqrt{2}}$

cos x = $\frac{1}{\sqrt{2}}$ger x = $\frac{\mathrm{\pi }}{4} och \frac{7\mathrm{\pi }}{4}$

cos x = -$\frac{1}{\sqrt{2}}$ger x = $\frac{3\mathrm{\pi }}{4} och \frac{7\mathrm{\pi }}{4}$

alla x-värden har perioden n*2$\mathrm{\pi }$

Hoppas det jag skrev blev rätt och går att följa.