Ange formel

Kan du ta reda på en formel som ger volymen för formen "Ett halvklot under en kon"?

Densitetens enhet är 

$\frac{g}{c{m}^3}$

 $$\begin{gathered} g\hspace{0.17em}= massa \left(gram\right) \\ c{m}^3 = volym \left(kubikcentimeter\right) \end{gathered}$$

Genom att multiplicera med densiteten med en volym får du kvar massan:

$\frac{g}{c{m}^3}·c{m}^{3 }=g$

Så du behöver alltså hitta volymen på diamanten. "Ett halvklot under en kon"

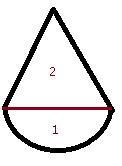
1: volym av halvklot

2: Volym av kon

Denna volym multiplicerar du på densiteten.

sprite111 skrev :

Kan du ta reda på en formel som ger volymen för formen "Ett halvklot under en kon"?

Densitetens enhet är 

$\frac{g}{c{m}^3}$

 $$\begin{gathered} g\hspace{0.17em}= massa \left(gram\right) \\ c{m}^3 = volym \left(kubikcentimeter\right) \end{gathered}$$

Genom att multiplicera med densiteten med en volym får du kvar massan:

$\frac{g}{c{m}^3}·c{m}^{3 }=g$

 

Så du behöver alltså hitta volymen på diamanten. "Ett halvklot under en kon"

1: volym av halvklot

2: Volym av kon

 

Denna volym multiplicerar du på densiteten.

Hur +ar jag ihop B*h/3+pi*r^2/3*3,51?

Ser uppgiften ut sådär eller saknas det något?

Saknas kanske denna figur?

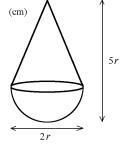
sprite111 skrev :

Ser uppgiften ut sådär eller saknas det något?

Saknas kanske denna figur?

ja exakt

Någon som kan?

Volymen för en kona: $\frac{1}{3}\mathrm{\pi } {\mathrm{r}}^2 \mathrm{h}$

Volymen för ett halvklot: $\frac{2\mathrm{\pi } {\mathrm{r}}^3}{3}$.

Konans diameter är 2r, alltså blir radien bara r.

Samma radie gäller för halvklotet.

När jag adderar volymerna får jag: 

3.67566 h r^2 + (2 π r^3)/3

Frågan är vad ska höjden på konan vara.

sprite111 skrev :

Någon som kan?

 

Volymen för en kona: $\frac{1}{3}\mathrm{\pi } {\mathrm{r}}^2 \mathrm{h}$

Volymen för ett halvklot: $\frac{2\mathrm{\pi } {\mathrm{r}}^3}{3}$.

 

Konans diameter är 2r, alltså blir radien bara r.

Samma radie gäller för halvklotet.

 

När jag adderar volymerna får jag: 

3.67566 h r^2 + (2 π r^3)/3

Frågan är vad ska höjden på konan vara.

Är inte h=3r på konen?

lamayo skrev :

sprite111 skrev :

Någon som kan?

 

Volymen för en kona: $\frac{1}{3}\mathrm{\pi } {\mathrm{r}}^2 \mathrm{h}$

Volymen för ett halvklot: $\frac{2\mathrm{\pi } {\mathrm{r}}^3}{3}$.

 

Konans diameter är 2r, alltså blir radien bara r.

Samma radie gäller för halvklotet.

 

När jag adderar volymerna får jag: 

3.67566 h r^2 + (2 π r^3)/3

Frågan är vad ska höjden på konan vara.

Är inte h=3r på konen?

Blir det inte 4*pi*2^3/6=2/3*pi*r^3=?     och B*h/3=pi*2r*3r/3=2pi*r

Vet faktiskt inte, borde ju vara att bara ta, volymen för konen + volymen för halvklotet där man har rätt höjd på konen. Sen multiplicerar man med densiteten. 

Får dock inte till det av någon anledning. Ska testa en gång till.

Någon som kan lösa uppgiften?

När jag adderar volymerna och sätter h=3r får jag

$\frac{5\mathrm{\pi } {\mathrm{r}}^3}{3}$

.

Tydligen ska h var = 4r.

För när jag sätter h = 4r får jag 7.02Pi*r^3

Ja, om vi tänker att klotets diameter är 2r, blir dess radie r. 

5r-r = 4r.

$$\begin{gathered} (\frac{1\mathrm{\pi } {\mathrm{r}}^2 ·\mathrm{h}}{3} + \frac{2 \mathrm{\pi } {\mathrm{r}}^3}{3}) \\ Sätter vi h = 4r (konens höjd): \\ (\frac{{\displaystyle 1\mathrm{\pi } {\mathrm{r}}^2 ·4r}}{{\displaystyle 3}} + \frac{{\displaystyle 2 \mathrm{\pi } {\mathrm{r}}^3}}{{\displaystyle 3}}) fås volymen: \\ 2\mathrm{\pi } {\mathrm{r}}^3 \\ 2 \mathrm{\pi } {\mathrm{r}}^3*3.51 = 7.02*\mathrm{\pi } {\mathrm{r}}^3 \end{gathered}$$

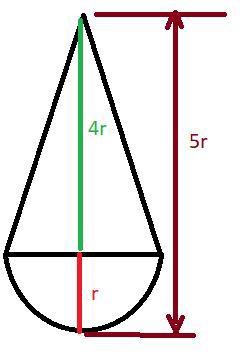
sprite111 skrev :

Ja, om vi tänker att klotets diameter är 2r, blir dess radie r. 

5r-r = 4r.

$$\begin{gathered} (\frac{1\mathrm{\pi } {\mathrm{r}}^2 ·\mathrm{h}}{3} + \frac{2 \mathrm{\pi } {\mathrm{r}}^3}{3}) \\ Sätter vi h = 4r (konens höjd): \\ (\frac{{\displaystyle 1\mathrm{\pi } {\mathrm{r}}^2 ·4r}}{{\displaystyle 3}} + \frac{{\displaystyle 2 \mathrm{\pi } {\mathrm{r}}^3}}{{\displaystyle 3}}) fås volymen: \\ 2\mathrm{\pi } {\mathrm{r}}^3 \\ 2 \mathrm{\pi } {\mathrm{r}}^3*3.51 = 7.02*\mathrm{\pi } {\mathrm{r}}^3 \end{gathered}$$

Från början hur blir diametensvikt hela kroppens massa? Sedan hur blir det när du plusar ihop de? alltså 2/3*pi*r^3+1/3*pi*r^2*4r? Sedan hur kan du gångra när det är r^3?

Volym * Densitet = Massa. Detta kan visas genom att skriva ut enheterna:

Volym har enheten:  cm^3 (kubikcentimeter). (x^3 (kan vara kubikmeter osv, men i detta fall används cm^3 eftersom vi har densiteten i g/cm^3)

Densiteten har enheten: g/cm^3.

Genom att multiplicera volym med densitet fås enligt enheterna:

$c{m}^3·\frac{g}{c{m}^3} = g \left(gram\right)$ (alltså en massa).

----

Vi har de olika volymerna:

Konen: $V_1=\frac{1}{3}\mathrm{\pi } {\mathrm{r}}^2 \mathrm{h} = \{\mathrm{h}=4\mathrm{r}\} = \frac{1}{3}\mathrm{\pi } {\mathrm{r}}^2 4\mathrm{r}.$

Halvklotet: $V_2=\frac{2}{3} \mathrm{\pi } {\mathrm{r}}^3$

Adderar (plussar) vi volymerna fås volymen för föremålet ($V_1+V_2$).

Additionen görs på följande sätt.

Vi har från början:

$\frac{1}{3}\pi r^2*4r+\frac{2}{3}\pi r^3$

Detta kan skrivas om på följande sätt:

 $\frac{1}{a}(b·c)=\frac{b·c}{a}$. I vårt fall innebär det:

 $\frac{\pi r^2·4r}{3}+\frac{2\pi ·r^3}{3}$.

Vi kan ytterligare skriva om lite till om vi vill till: (notera vänstra termens täljare 4 flyttades fram)

$\frac{4\pi r^{2}r}{3}+\frac{2\pi r^3}{3}$.

Detta görs enligt regeln som kallas kommutativa lagen och säger:

$$\begin{gathered} a·b=b·a, \\ a·b·c=c·a·b \end{gathered}$$ 

Alltså multiplikation av två tal (eller 3 eller flera) kan skrivas om enligt ovan.

--

Om vi kollar på första termen (den till vänster) ser vi att vi har

$r^2·r$. Detta kan enligt potensreglerna skrivas om enligt följande:

$a^x·a^y=a^{x+y}$. Multiplicerar man två likadana baser adderas exponenterna. I vårt fall blir det:

$r^2·r^1=r^{2+1}=r^3$.

Detta ger oss nu:

$\frac{4\pi r^3}{3}+\frac{2\pi r^3}{3}$

Vi noterar att vi har gemensam nämnare och kan därför addera bråken enligt följande regel:

$\frac{a}{b}+\frac{c}{b}\text{=}\frac{a+c}{b}$. Två bråk kan adderas/subtraheras när de har gemensam nämnare (nämnaren förblir den samma medan täljarna adderas). I vårt fall ger det:

$\frac{4\pi r^3+2\pi r^3}{3}$.

Vi kan sedan addera i täljaren enligt följande:

4x +2x = 6x. I detta fallet har vi: $4\pi r^3+2\pi r^3=6\pi r^3$. Vilket ger:

$\frac{6\pi r^3}{3}$.

Vi kan sedan förenkla: 

$\frac{6}{3}\pi r^3=2\pi r^3$

Volymen för hela föremålet är alltså: $2\pi r^3$.

---

Ser vi till det vi gjorde ovan med enheterna och fick fram:

Volym * Densitet = Massa. Detta innebär i vårt fall:

$2\pi r^3·3.51=7.02\pi r^3$.

$\mathbf{2}\mathbf{}\mathit{\pi }\mathbf{}{\mathit{r}}^{\mathbf{3}}$ är volymen.

3. 51 är densiteten.

.

sprite111 skrev :

Volym * Densitet = Massa. Detta kan visas genom att skriva ut enheterna:

Volym har enheten:  cm^3 (kubikcentimeter). (x^3 (kan vara kubikmeter osv, men i detta fall används cm^3 eftersom vi har densiteten i g/cm^3)

Densiteten har enheten: g/cm^3.

Genom att multiplicera volym med densitet fås enligt enheterna:

$c{m}^3·\frac{g}{c{m}^3} = g \left(gram\right)$ (alltså en massa).

----

Vi har de olika volymerna:

Konen: $V_1=\frac{1}{3}\mathrm{\pi } {\mathrm{r}}^2 \mathrm{h} = \{\mathrm{h}=4\mathrm{r}\} = \frac{1}{3}\mathrm{\pi } {\mathrm{r}}^2 4\mathrm{r}.$

Halvklotet: $V_2=\frac{2}{3} \mathrm{\pi } {\mathrm{r}}^3$

Adderar (plussar) vi volymerna fås volymen för föremålet ($V_1+V_2$).

Additionen görs på följande sätt.

Vi har från början:

$\frac{1}{3}\pi r^2*4r+\frac{2}{3}\pi r^3$

Detta kan skrivas om på följande sätt:

 $\frac{1}{a}(b·c)=\frac{b·c}{a}$. I vårt fall innebär det:

 $\frac{\pi r^2·4r}{3}+\frac{2\pi ·r^3}{3}$.

Vi kan ytterligare skriva om lite till om vi vill till: (notera vänstra termens täljare 4 flyttades fram)

$\frac{4\pi r^{2}r}{3}+\frac{2\pi r^3}{3}$.

Detta görs enligt regeln som kallas kommutativa lagen och säger:

$$\begin{gathered} a·b=b·a, \\ a·b·c=c·a·b \end{gathered}$$ 

Alltså multiplikation av två tal (eller 3 eller flera) kan skrivas om enligt ovan.

--

Om vi kollar på första termen (den till vänster) ser vi att vi har

$r^2·r$. Detta kan enligt potensreglerna skrivas om enligt följande:

$a^x·a^y=a^{x+y}$. Multiplicerar man två baser adderas exponenterna. I vårt fall blir det:

$r^2·r^1=r^{2+1}=r^3$.

Detta ger oss nu:

$\frac{4\pi r^3}{3}+\frac{2\pi r^3}{3}$

Vi noterar att vi har gemensam nämnare och kan därför addera bråken enligt följande regel:

$\frac{a}{b}+\frac{c}{b}\text{=}\frac{a+c}{b}$. Två bråk kan adderas/subtraheras när de har gemensam nämnare (nämnaren förblir den samma medan täljarna adderas). I vårt fall ger det:

$\frac{4\pi r^3+2\pi r^3}{3}$.

Vi kan sedan addera i täljaren enligt följande:

4x +2x = 6x. I detta fallet har vi: $4\pi r^3+2\pi r^3=6\pi r^3$. Vilket ger:

$\frac{6\pi r^3}{3}$.

Vi kan sedan förenkla: 

$\frac{6}{3}\pi r^3=2\pi r^3$

Volymen för hela föremålet är alltså: $2\pi r^3$.

---

Ser vi till det vi gjorde ovan med enheterna och fick fram:

Volym * Densitet = Massa. Detta innebär i vårt fall:

$2\pi r^3·3.51=7.02\pi r^3$.

 

$\mathbf{2}\mathbf{}\mathit{\pi }\mathbf{}{\mathit{r}}^{\mathbf{3}}$ är volymen.

3. 51 är densiteten.

.

Tack för en väldigt bra förklaring! nu förstår jag!:) 

Obs ovan ska stå Multiplicerar man två likadana baser adderas exponenterna (redigerar nu)

a^x * a^y = a^(x+y)

Alltså funkar det inte på a^x * b^y!!!

sprite111 skrev :

Obs ovan ska stå Multiplicerar man två likadana baser adderas exponenterna (redigerar nu)

 

a^x * a^y = a^(x+y)

 

Alltså funkar det inte på a^x * b^y!!!

okej