Ange om möjligt f invers och dess matris

Hej jag vet inte riktigt hur jag ska gå tillväga på denna
jag har ritat upp grafen till matrisen som visas nedan och får det till två grafer som inte sitter ihop
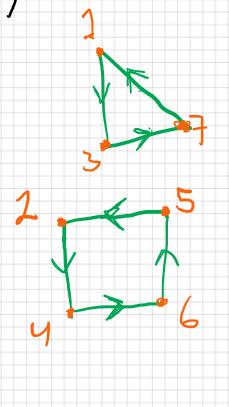
men funktionerna till matrisen är den f(1)=3, f(3)=7 och f(7)=1
och f(2)=4, f(4)=6,f(6)=5 och f(5)=2
och skulle inversen till funktionen exempel bli f(1)=3 -> f(3)=1?
tack på förhand
Jag gissar att det är som du skriver (förutom att det borde vara f-1(3)=1 på slutet.
Det går förstås inte alltid att göra en funktion av en riktad graf.
Laguna skrev:Jag gissar att det är som du skriver (förutom att det borde vara f-1(3)=1 på slutet.
Det går förstås inte alltid att göra en funktion av en riktad graf.
okej tack så mycket!
jag har fastnat på b nu och förstår inte riktigt när n>1 så att
???
Alligatoraffe skrev:Laguna skrev:Jag gissar att det är som du skriver (förutom att det borde vara f-1(3)=1 på slutet.
Det går förstås inte alltid att göra en funktion av en riktad graf.
okej tack så mycket!
jag har fastnat på b nu och förstår inte riktigt när n>1 så att
???
Lättast är att utnyttja grafen.
f^n motsvarar att gå n steg i grafen.
Kan du hitta ett n sådant, att oavsett var du börjar, så slutar du där du börjar efter n steg?
Exvis: om du börjar i nod 1 så slutar du där du börjar om n=3. Men om du börjar i nod 4 så slutar du där du börjar om n=4. Finns det ett n som gör att du slutar där du börjar oavsett där du börjar?
Äsch ser nu att tråden är uråldrig.



