Ange värdet på a
Hej! Jag hade behövt lite hjälp med följande fråga, det har tagit lite stopp i huvudet på mig så jag vet inte riktigt hur jag ska gå tillväga.
för a-uppgiften tänker jag att om man skulle skriva om det uttrycket som pq-formeln så måste diskriminanten vara större än noll för att ekvationen ska ha 2 lösningar.
För b-uppgiften tänker jag att man kan kvadrera och på något vis räkna fram värdet på a.
på c tänker likt första uppgiften men att diskriminanten ska vara mindre än a.
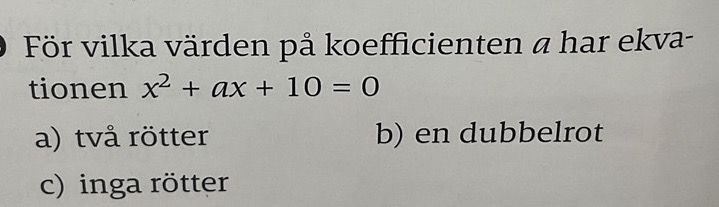
Det kan vara fel tanke på metoder och kanske det som gör att jag inte vet hur jag ska räkna, eller så är jag lite trött, så jag hade varit väldigt tacksam för all hjälp jag kan få :)
Du tänker helt rätt:
D>0: två reella rötter
D=0: en reell dubbelrot
D<0: inga reella rötter (två komplexa rötter)
Diskriminanten D är alltså uttrycket under rottecknet i pq-formeln, bara så vi talar om samma sak.
Jajamän! Det hängde jag med på. Jag gjorde ett försök på att lösa uppgiften en gång till och kom då fram till lite vettigare svar, men när jag kom till c-uppgiften gick något snett, för olikheten är inte rimlig (det är det blåmarkerade) JAg försökte förstå mig på hur den olikheten hade sett ut på en tallinje bara för att få det lite tydligare, men det visade ännu mer på att något var fel. Eller så är det fel på det jag ritat. Eller vem vet, kanske båda.

Bra att du tänker tallinje!
Förvirringen kommer sig kanske av att ditt svar på (a) inte är rätt. När a är >-√40 har du gått till höger på tallinjen.
D>0 när a<-√40 eller när a>√40. Notera tecknen! Alternativt när |a|>√40 (om ”beloppet av” är bekant). Det är alltså ytterkanterna till vänster och höger på din tallinje.
Det komplexa området utan reella lösningar är det i mitten: -√40<a<√40.
Dubbelroten har du prickat: a=+/- √40. Det är punkterna mitt emellan som du markerat.
Bra tänkt och ritat!
Tack! Jag tror jag förstår det mesta av det du förklarar. Dock förstår jag inte hur det i a-uppgiften kan bli ett sådant svar, där a egentligen ligget på det motsatta intervallet för det komplexa orådet. Alltså . Eller jag förstår ju varför det gäller, för det är de reella lösningarna och därav på ytterkanterna, så det i sig är logiskt, men hur man algebraiskt kommer fram till det intervallet från en ekvation som började som en enda olikhet hänger jag inte riktigt med på. Hoppas det går att förstå min fråga, inte alltid lätt att sätta ord på vad det är man inte helt förstår :)
Du har satt minustecknet fel, men jag tror jag förstår och vi menar samma sak.
Regel: När man multiplicerar eller dividerar en olikhet med ett negativt tal, måste man vända på olikhetstecknet.
Om a2>40 så betyder det att a skall vara på längre avstånd än √40 från nollan, om man tittar på tallinjen. Det blir alltså a>√40, men däremot a<-√40.
Jag kan försöka förklara det bättre. Fråga på!
Det kan jag säga är en regel jag helt och hållet glömt bort sedan matte 1, tack för den påminnelsen :)
Och om jag förstått dig rätt för det sista där tecknet vänds för -eftersom att det är som om det skulle vara (-a)^2 så skulle också roten ur 40 multipliceras med -1 och därav orsaka vändningen på olikhetstecknet. Det var itne den bästa förklaringen och jag får dessutom en känsla av att jag bryter mot någon annan regel när jag säger att a multipliceras med -1 när den står i kvadrat. Jag förstår din idé men jag vet inte hur jag matematiskt kan redovisa att jag förstått, för du måste väl multiplicera med -1 för att få -, men gör jag något i ena ledet måste jag självklart göra det i andra ledet också.
Kvadratrötter och absolutbelopp hänger ihop. Jag kanske inte borde ha nämnt multiplikation med -1 för det är inte vad som händer.
Ta en titt: https://www.matteboken.se/lektioner/gymnasiet/matte-fortsattning-niva-1/algebraiska-uttryck/absolutbelopp
Förvisso står det som Ma3, men ändå.
Tidigare har jag bara hört absolutbelopp i samband med vektorer, men visste inte att kvadratrötter och absolutbelopp hängde ihop förrän nu. Menade du alltså att -har samma absolutbelopp som ?
KlmJan skrev:Tidigare har jag bara hört absolutbelopp i samband med vektorer, men visste inte att kvadratrötter och absolutbelopp hängde ihop förrän nu. Menade du alltså att -har samma absolutbelopp som ?
Japp!
Absolutbeloppet anger avståndet från noll.
Det är längden av en vektor oavsett tecken. Om du backar har du kanske hastigheten -20 km/h (riktat bakåt), men din fart är |v|=20 km/h.
Kort sagt: absolutbeloppet stryker minustecknet.
|-1| = 1
Ok, skönt att jag har förstått det nu, men om vi återgår till frågan, kan man alltså säga att a är absolutbeloppet av de två kvadratrötterna? Och att det är därför a förblir positivt men olikhetstecknet vänder håll för för ursprungligen var det ju a2=40 vilket gav oss en positiv och negativ rot.
Man kan säga att |a|>√40, vilket innebär att a kan vara positivt och negativt. Vad gäller a2 så gäller >40, vilket är samma sak.
Kvadratroten blir alltid positiv. Att ta något i kvadrat ger också alltid ett positivt resultat. Saken är att när du tar a2 så försvinner informationen vilket tecken a hade.
Det är det du måste ta hänsyn till när du svarar. Antingen fixar du det med absolutbelopp eller med två uttryck för a. Det finns ingen klockren algebraisk väg.


