Ange en formel för u_n som en funktion av n

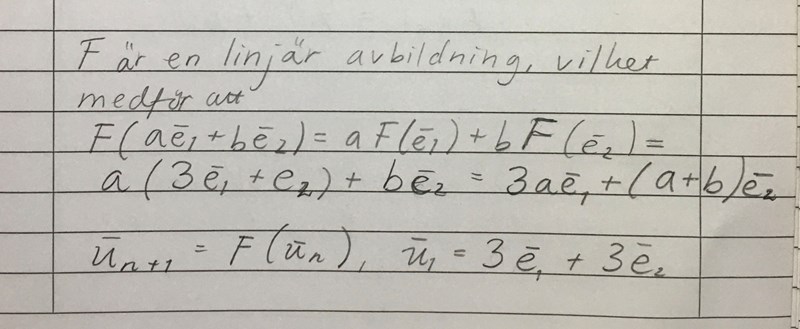
Jag skulle börja med att hitta matrisen till den linjära avbildningen F. Kan du göra det?

Du kan ju börja med att räkna ut $u_1$, $u_2$, $u_3$, $u_4$och se om du ser något mönster i talen.

Ska det vara $3e_1 + e_1$ eller $3e_1 + e_2$?

När du hittat matrisen för avbildningen (A) kan du diagonalisera $A=TDT^{-1}$

Notera nu att

$AA=TDT^{-1}TDT^{-1}=TD^2T^{-1}$ osv

$A_1....A_n=TD^nT^{-1}$

Det ska vara 3e_1 + e_2

Matrisen till den linjära avbildningen F är

3  0

1  1

Vi kallar matrisen A och nu ska jag diagonalisera den, men är inte riktigt säker på hur?

Steg 1 är att ta fram egenvärdena. Notera att din matris är triangulär

Ok, först egenvärdena.

En triangulär matris är en matris som har enbart nollor på ena sidan om diagonalen.

Egenvärdena för en triangulär matris är lika med elementen på diagonalen, vilket ger oss egenvärdena 3, 1.

Stämmer detta?

Javisst, det ser helt korrekt ut. Eftersom du har två olika egenvärden kan du vara helt säker på att diagonalisering är möjlig, men då behöver du två linjärt oberoende egenvektorer(i detta fall från två olika egenrum hörande till respektive egenvärden). Kan du hitta dessa egenvektorer?

Vi har två egenvärden, ${\lambda }_1=3$ och ${\lambda }_2=1$.

När man har egenvärdena ska man stoppa in dessa i ekvationen $(A-\lambda I)\overrightarrow{v}=\overrightarrow{0}$ , ett egenvärde i taget, för att räkna ut egenvektorerna.

För ${\lambda }_1$ har vi $\left[\begin{array}{cc}3-3& 0\\ 1& 1-3\end{array}\right]\overrightarrow{v}=\left[\begin{array}{c}0\\ 0\end{array}\right] \iff \left[\begin{array}{cc}0& 0\\ 1& -2\end{array}\right]\overrightarrow{v}=\left[\begin{array}{c}0\\ 0\end{array}\right]$

Om jag GJ-eliminerar 2x2-matrisen ser den ut som $\left(\begin{array}{cc}1& -2\\ 0& 0\end{array}\right)$ vilket ger lösningen $x-2y=0$ vilket i sin tur ger egenvektorn $\left[\begin{array}{c}2\\ 1\end{array}\right]$.

När jag gör på samma sätt för ${\lambda }_2$ får jag $\left[\begin{array}{cc}3-1& 0\\ 1& 1-1\end{array}\right]\overrightarrow{v}=\left[\begin{array}{c}0\\ 0\end{array}\right] \iff \left[\begin{array}{cc}2& 0\\ 1& 0\end{array}\right]\overrightarrow{v}=\left[\begin{array}{c}0\\ 0\end{array}\right]$.

Om jag GJ-eliminerar 2x2-matrisen ser den ut som $\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right)$  vilket ger lösningen $x=0$ vilket i sin tur ger egenvektorn $\left[\begin{array}{c}0\\ 0\end{array}\right].$

Har jag gjort rätt? Och är egenvektorerna $\left[\begin{array}{c}2\\ 1\end{array}\right]$ och $\left[\begin{array}{c}0\\ 0\end{array}\right]$?

Egenvektorer är per definition skilda från noll. Så något har gått fel.

Jag skulle även vilja räkna ut $u_1, u_2, u_3, u_4...$ och se om jag hittar något mönster. Men jag är osäker på hur jag ska börja.

Kan någon hjälpa mig att komma igång?

Vi har att $u_1= 3e_1+3e_2$

och att $$\begin{gathered} u_{n+1}= F\left(u_n\right)=a_{n+1}{e}_1+b_{n+1}{e}_2 = F(a_n{e}_1+b_n{e}_2)=3a_n{e}_1+(a_n+b_n)e_2. \\ {a}_{n+1}=3a_n, {\mathit{a}}_{\mathbf{1}}\mathbf{=}\mathbf{?} \end{gathered}$$

Vad är $a_1$?

Ja, jag förstod nästan att jag gjort något fel när en av egenvektorerna blev nollvektorn.

Kan någon hjälpa mig se vad som blev tokigt?

Du får villkoret att x = 0, men inget villkor på y, förutom att y inte får vara noll förstås.

Så $\left[\begin{array}{c}0\\ 1\end{array}\right]$ ser ut att funka, men dubbelkolla att $\left[\begin{array}{cc}3& 0\\ 1& 1\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]$ = $\left[\begin{array}{c}0\\ 1\end{array}\right]$.

Men A *(egenvektorn)

ska väl resultera i nollvektorn?

Nej. Ax = $\lambda$x. Så är egenvärdesproblemet. $\iff$ (A - $\lambda$I)x = 0.

Ja, men då stämmer det. Då har vi två korrekta egenvektorer. Dessa är $\left[\begin{array}{c}2\\ 1\end{array}\right]$ och $\left[\begin{array}{c}0\\ 1\end{array}\right]$.

Så nu har jag tagit fram egenvärden, därefter egenvektorerna och nu ska jag alltså diagonalisera?

Jag förstår att det måste vara av värde att veta koordinaterna för $u_1$ också, vilka är (3,3). Vi kan se även dem som en kolonnvektor $\left[\begin{array}{c}3\\ 3\end{array}\right]$. Hur kan jag nu använda detta?

(Jag påstår att kolonnvektorn för $u_1$ är $\left[\begin{array}{c}3\\ 3\end{array}\right]$ eftersom $u_1= 3e_1+3e_2$.)

Jag försöker även parallellt att arbeta med uppgiften genom att definiera en geometrisk talföljd för ${\mathit{a}}_{\mathbf{n}}$.

Jag tror att $a_{n+1}=3a_n$, där $a_1= 3.$

Detta baserar jag på att $F\left(e_1\right)=3e_1+e_2$ och att $u_1=3e_1+3e_2$.  Har jag rätt där? 
Mitt förslag på rekursiv talföljd:

Jag hoppas att ni gått igenom egenvärden, egenvektorer och diagonalisering  i er kurs och att du har ett avsnitt om diagonalisering kurslitteraturen. Lite repetition

Om $n\times n$ matrisen A har n stycken linjärt oberoende egenvektorer $\mathbf{e_i}$ med tillhörande egenvärden $\lambda_i$ gäller att:

$T^{-1}AT=D$

Där T:s kolonner utgörs av egenvektorerna, dvs

$T=(\mathbf{e}_1,\mathbf{e}_2,\dots,\mathbf{e}_n)$

Och där D är diagonalmatrisen

$D=\begin{bmatrix}\lambda_1 & 0 &\dots & 0\\0 & \lambda_2 & \dots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0&\dots & \lambda_n \end{bmatrix}$

($\mathbf{e}_i$ och $\lambda_i$ kan vara reella eller komplexa, liksom A) 

Sätter man in dina värden i T och D  (och inverterar T, notera att $2 \times 2$-matriser är enkla att invertera) får man:

$A=TDT^{-1}=\begin{bmatrix}2&0\\1&1\end{bmatrix}\begin{bmatrix}3&0\\0&1\end{bmatrix}\begin{bmatrix}\frac{1}{2}&0\\-\frac{1}{2}&1\end{bmatrix}$

Nu är $A^n$ enkel att beräkna, allt du behöver göra är att beräkna $D^n$

$A_1A_2\dots A_n=\begin{bmatrix}2&0\\1&1\end{bmatrix}\begin{bmatrix}3^n&0\\0&1^n\end{bmatrix}\begin{bmatrix}\frac{1}{2}&0\\-\frac{1}{2}&1\end{bmatrix}$

Tack Jroth.

Då får jag att 

$A_n=\left[\begin{array}{cc}{3}^{n-1}& 0\\ \left(3^{n-1}\right)/2& 1\end{array}\right]$.

Nu vill jag hitta koordinaterna för $u_n$. 

Då multiplicerar jag matrisen $A_n$ med kolonnvektorn $\left[\begin{array}{c}3\\ 3\end{array}\right]$.

$\left[\begin{array}{cc}{3}^{n-1}& 0\\ \left(3^{n-1}\right)/2& 1\end{array}\right]\left[\begin{array}{c}3\\ 3\end{array}\right]=\left[\begin{array}{c}{3}^n\\ \frac{3^n+3}{2}\end{array}\right],$ vilket betyder att $a_n=3^n$ och $b_n=\frac{3^n+3}{2}$.

Så vi har nu koordinaterna för $u_n$ i basen $e_1, e_2.$

${\mathit{u}}_{\mathbf{n}}\mathbf{=}{\mathbf{3}}^{\mathbf{n}}\mathbf{·}{\mathit{e}}_{\mathbf{1}}\mathbf{+}\frac{{\mathbf{3}}^{\mathbf{n}}\mathbf{+}\mathbf{3}}{\mathbf{2}}\mathbf{·}{\mathit{e}}_{\mathbf{2}}.$