Anpassa en linjär,kvadratisk och exponentiell funktion till värdena.
 Hej!
Hej!
Jag har svarat på linjära och exponentiell, är det stämmer??? Kvadratisk vet jag inte 🤷♂️ tack för svar och hjälpen!
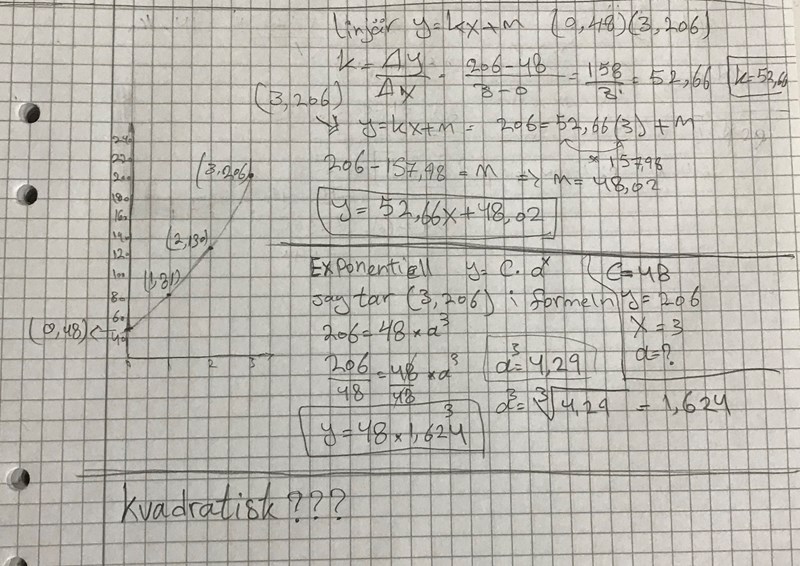
Det finns olika metoder man kan använda och jag vet inte vilka man går igenom i Ma2. Det du har gjort är rätt om det är meningen att man ska använda den enklaste metoden - dvs man väljer några punkter och anpassar till dem.
Sedan finns det andra metoder som minsta kvadratmetoden. Om ni har gått igenom den borde du använda den, men då behöver du ha en miniräknare eller kalkylprogram som kan göra det.
En kvadratisk funktion är ett annat namn på en andragradsfunktion, dvs
SvanteR skrev:Det finns olika metoder man kan använda och jag vet inte vilka man går igenom i Ma2. Det du har gjort är rätt om det är meningen att man ska använda den enklaste metoden - dvs man väljer några punkter och anpassar till dem.
Sedan finns det andra metoder som minsta kvadratmetoden. Om ni har gått igenom den borde du använda den, men då behöver du ha en miniräknare eller kalkylprogram som kan göra det.
En kvadratisk funktion är ett annat namn på en andragradsfunktion, dvs
Hej SvanteR!
Tack för svar. jag vet formeln till andragradsfunktion och med min grafräknare jag kan hitta talen men jag vill vet hur man med hand och skrivning lika som linjär och exponentiell kan visa.
De värdena från linjär och exponentiell som jag har löst, har lite skillnad med facit också.
Att det är skillnad mellan dina svar och facit beror antagligen på metoden. Prova att använda din grafräknare i stället och se om du får samma som facit.
Om du ska anpassa en andragradsfunktion "för hand" får du välja tre punkter och sätta in dem. Om jag till exempel väljer punkten (1, 81) får jag:
Sedan väljer man två andra punkter och får ett ekvationssystem med tre obekanta. Genom att lösa det får du värden på a, b och c. I den har uppgiften har du med en punkt där x=0, vilket underlättar!
SvanteR skrev:Att det är skillnad mellan dina svar och facit beror antagligen på metoden. Prova att använda din grafräknare i stället och se om du får samma som facit.
Om du ska anpassa en andragradsfunktion "för hand" får du välja tre punkter och sätta in dem. Om jag till exempel väljer punkten (1, 81) får jag:
Sedan väljer man två andra punkter och får ett ekvationssystem med tre obekanta. Genom att lösa det får du värden på a, b och c. I den har uppgiften har du med en punkt där x=0, vilket underlättar!
Jag har valt (0,48) 0ck (2,130).
48=a*02+b*0+C.
130=a*22+b*2+3.
a+b+c=48
4a+2b+c=130 den här ekvation systemmet har fått men om det är rät, hur kan kommer vidare?
Nja, vad blir a*0 och b*0 ;)
Som SvanteR skrev, du behöver välja 3 punkter om du vill anpassa en andragradskurva, eftersom det finns 3 olika konstanter i uttrycket f(x)=ax2+bx+c.
SvanteR skrev:Nja, vad blir a*0 och b*0 ;)
De blir 0. men så fall om a och b vilka tal är som helst svaret blir 0. men i en fall bara svaret blir 48 att c=48.
så det bli ax2+bx+48=48 eftersom x=0.
ekvationsystemet blir
a+b+48=48
4a+2b+48=130
andra punkt kan vara (1,81)
a+b+48=81.
är det stämmer??
Det stämmer att c=48
Ekvationen a+b+48=48 är fel.
Ekvationerna 4a+2b+48=130 och a+b+48=81 är rätt, de kan du använda för att bestämma a och b!
SvanteR skrev:Det stämmer att c=48
Ekvationen a+b+48=48 är fel.
Ekvationerna 4a+2b+48=130 och a+b+48=81 är rätt, de kan du använda för att bestämma a och b!
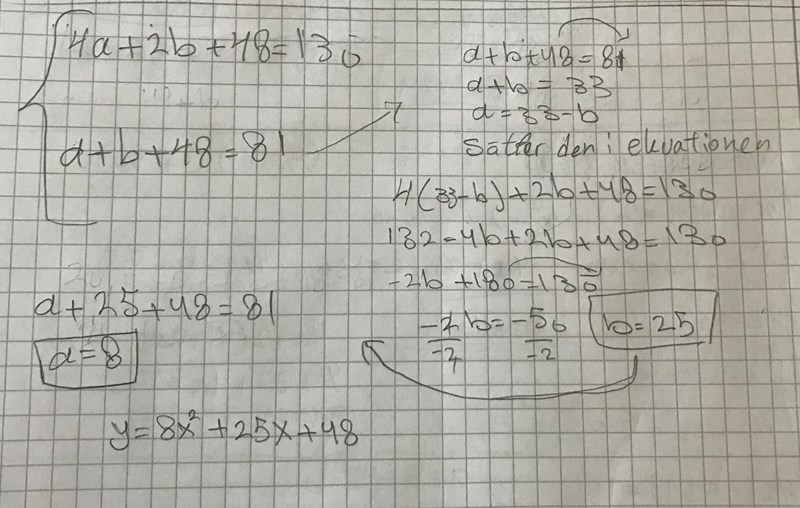 jag löst den på så sätt. Men på facit är y=10,75^2+20,5x+48. Vad jag har gjort fel?
jag löst den på så sätt. Men på facit är y=10,75^2+20,5x+48. Vad jag har gjort fel?
Hade du inte bild på kurvan tidigare? Pricka in värdena som din andragradsfunktion ger, och de som facits ger, så får vi se hur bra anpassningen är.
Du har gjort rätt enligt den metod som du har använt.
Men som jag har skrivit innan använder facit antagligen en annan metod. Jag gissar att det är den som finns programmerad i din räknare. Vet du hur du löser uppgiften med räknaren?
SvanteR skrev:Du har gjort rätt enligt den metod som du har använt.
Men som jag har skrivit innan använder facit antagligen en annan metod. Jag gissar att det är den som finns programmerad i din räknare. Vet du hur du löser uppgiften med räknaren?
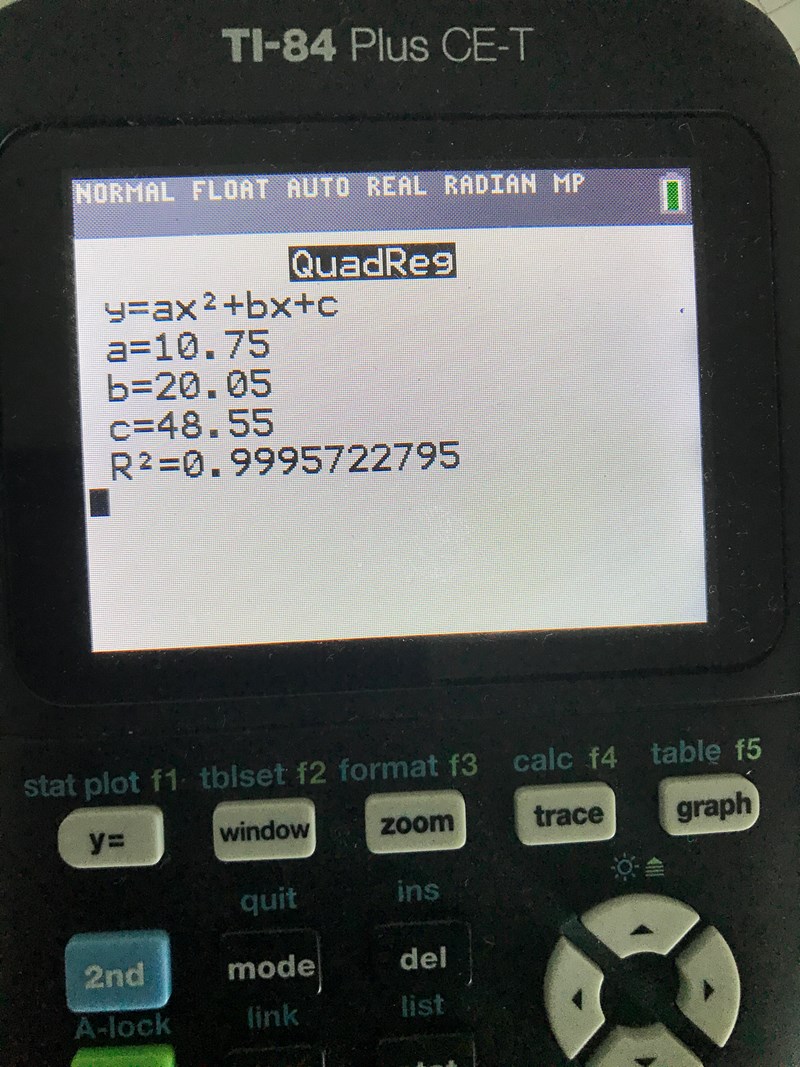
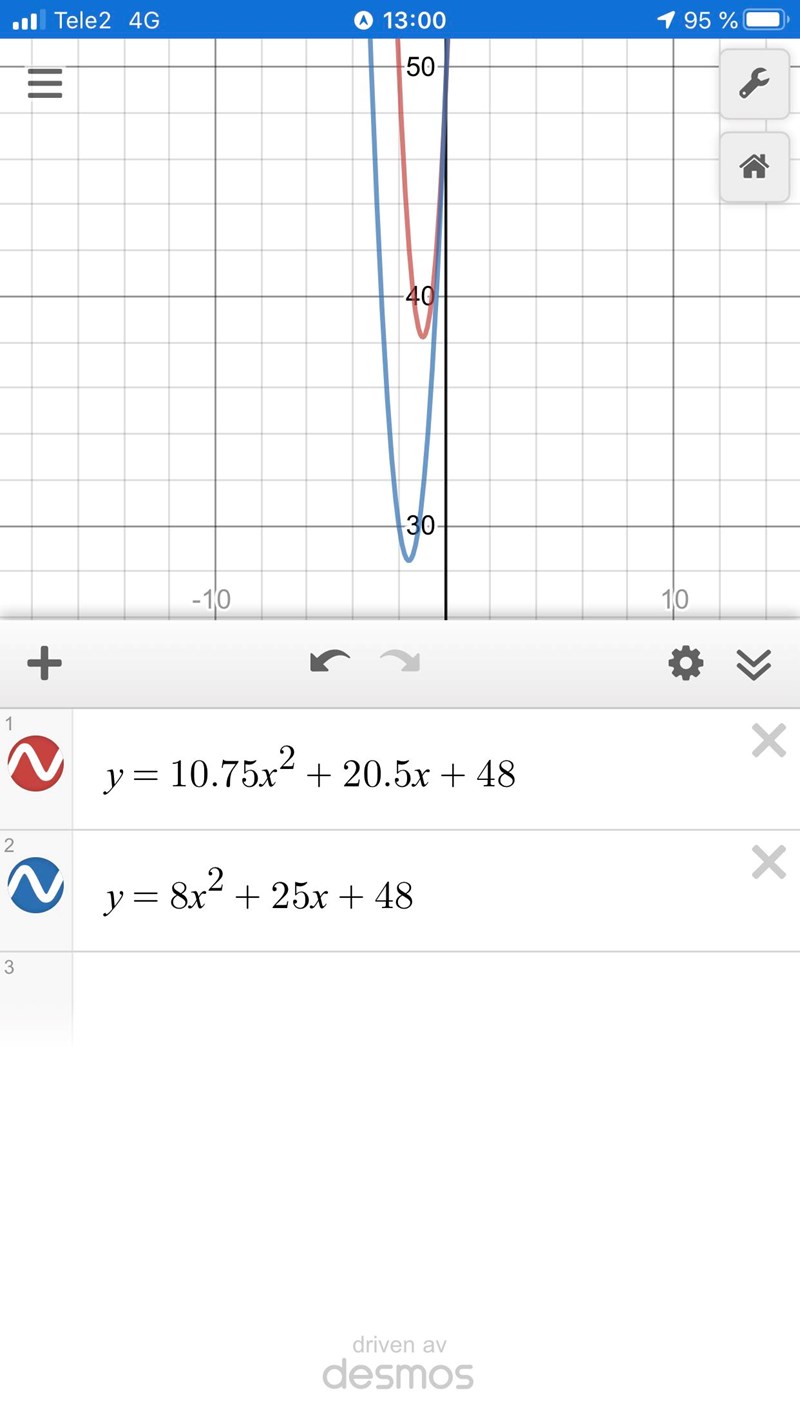 Det första bild har gjort med räknare, andra bild är kurvan med facit den röda , och min är blå.
Det första bild har gjort med räknare, andra bild är kurvan med facit den röda , och min är blå.
Det du får på din räknare är exakt samma som jag får när jag gör det i Excel (se bild). Jag vet inte hur de har gjort i ditt facit, men det finns som sagt många metoder och de kan ge lite olika resultat.
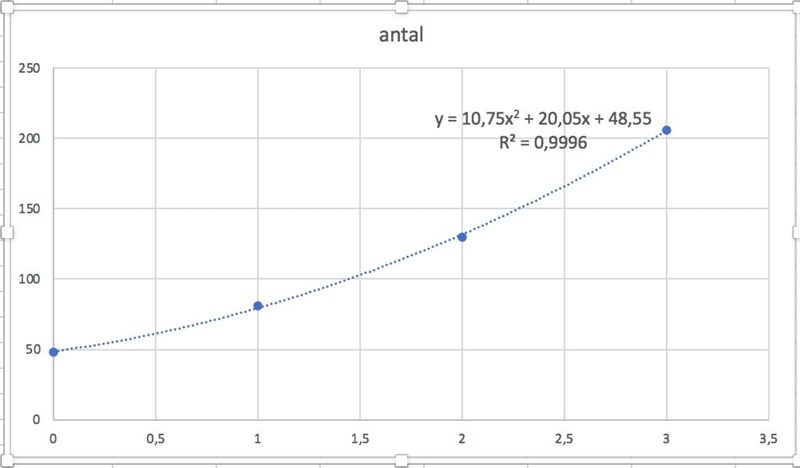
SvanteR skrev:Det du får på din räknare är exakt samma som jag får när jag gör det i Excel (se bild). Jag vet inte hur de har gjort i ditt facit, men det finns som sagt många metoder och de kan ge lite olika resultat.
Ja på facit är y=10,75x^2+20,05x+48.
men det som jag har löst har blivit y=8x^2+25x+48.
kurvan har jag själv skrivit i den här problemet och fått de här fugorna.
Jag är lite osäker på vad du menar? Är det något mer du undrar över?
SvanteR skrev:Jag är lite osäker på vad du menar? Är det något mer du undrar över?
Jag ville bara veta hur man för hand kan svara frågan andragradsekvation. Om du kolla från början jag har gjort exponentiellt och linjär metoden.
Här facit: 
och jag vill veta varför min lösning har inte blivit som facit?
facit: y=10,75x^2+20,05x+48,55
min: y=8x^2+25x+48.
När man ska anpassa en kurva till ett antal punkter kommer kurvan inte att passa perfekt. Om du ritar dina fyra punkter i ett diagram och försöker rita en linje i diagrammet kommer du att se att det är omöjligt att rita en linje som går genom alla fyra punkterna.
Det man gör i stället är att rita en linje som går så nära som möjligt. Den metod man oftast använder för att komma så nära som möjligt kallas minsta kvadratmetoden. Din miniräknare har den metoden inprogrammerad.
I den här uppgiften är det antagligen meningen att du ska använda den metoden. Du har i stället valt att använda en annan metod, där man väljer några punkter, anpassar en kurva till dem och hoppas att den kurvan kommer nära även de punkter man inte har valt. Så kan man också göra, men med den metoden får man ett annat resultat.
Freedom skrev:SvanteR skrev:Det du får på din räknare är exakt samma som jag får när jag gör det i Excel (se bild). Jag vet inte hur de har gjort i ditt facit, men det finns som sagt många metoder och de kan ge lite olika resultat.
Ja på facit är y=10,75x^2+20,05x+48.
men det som jag har löst har blivit y=8x^2+25x+48.
kurvan har jag själv skrivit i den här problemet och fått de här fugorna.
Hur kan man visa att den här linje och punkterna "för hand" blir y=10,75x^2+20,05x+48?
Det kräver en del matematik som man inte hinner med på gymnasiet. Du behöver i så fall förstå hur minsta kvadratmetoden fungerar, hur man använder den för en andragradskurva, och hur man ställer upp ett korrekt ekvationssystem. Du landar i det här (med andra beteckningar än du är van vid (a0 är det som vi har kallat c, a1 är b och a2 är a):
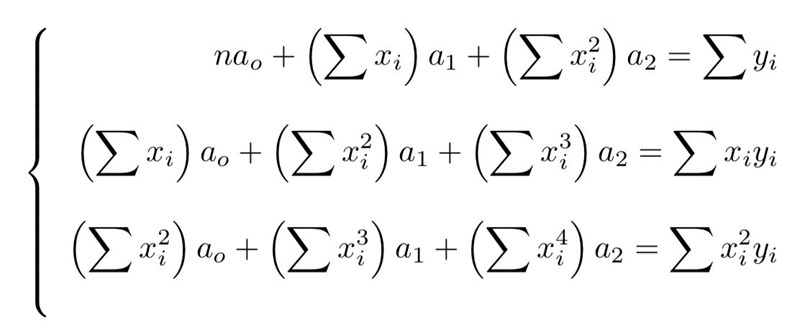
Vill du läsa mer finns det en genomgång här:
Det blir väldigt mycket räknande om man ska göra det för hand, så därför använder folk datorprogram i stället. Du har ett sådant program i din miniräknare!




