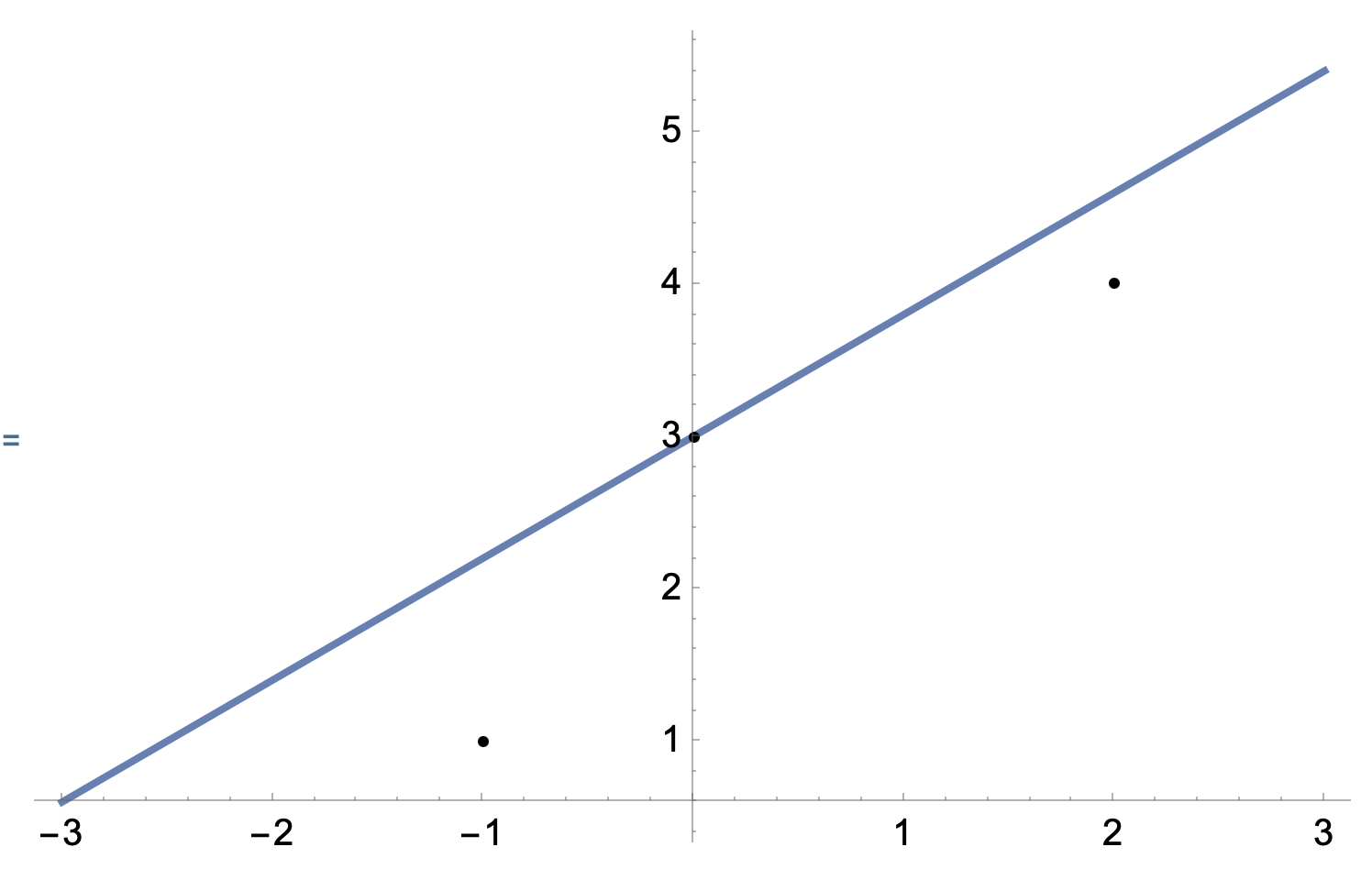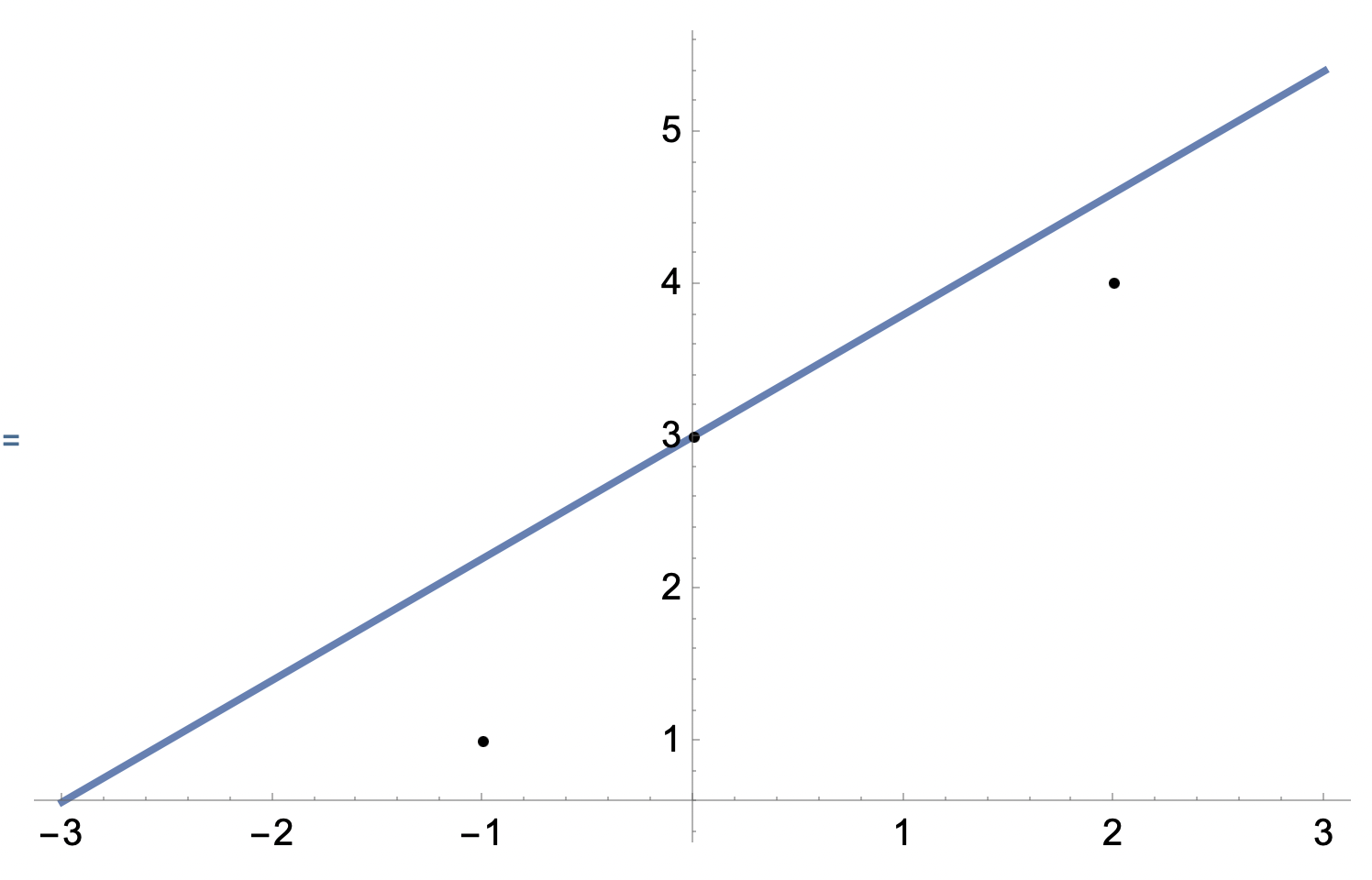Anpassning av en rät linje

OskarT skrev:

Uppgift:

Vi vill göra en anpassning med en rät linje till de tre punkterna (x1, y1) = (−1, 1), (x2, y2) = (0, 3) och (x3, y3) = (2, 4).

Vi antar nu att de tre punkterna är mätdata där den andra punkten är betydligt mer noggrant bestämd än de båda övriga punkterna. Bestäm den räta linje y = kx + m som passerar genom punkten (x2, y2) och anpassar till de båda andra punkterna i minstakvadratmening.


Hur långt jag har kommit:

Jag har kommit fram till att en linje som anpassar sig till alla tre punkter utan att gå genom (x2, y2) har ekvationen $y = \frac{13x}{14} + \frac{33}{14}$. Vet ej hur jag ska göra vidare.

Jag skulle tro att de vill att du skall minimera avstånden enl. minsta kvadratmetoden.

Jag får y=4/5 x+3

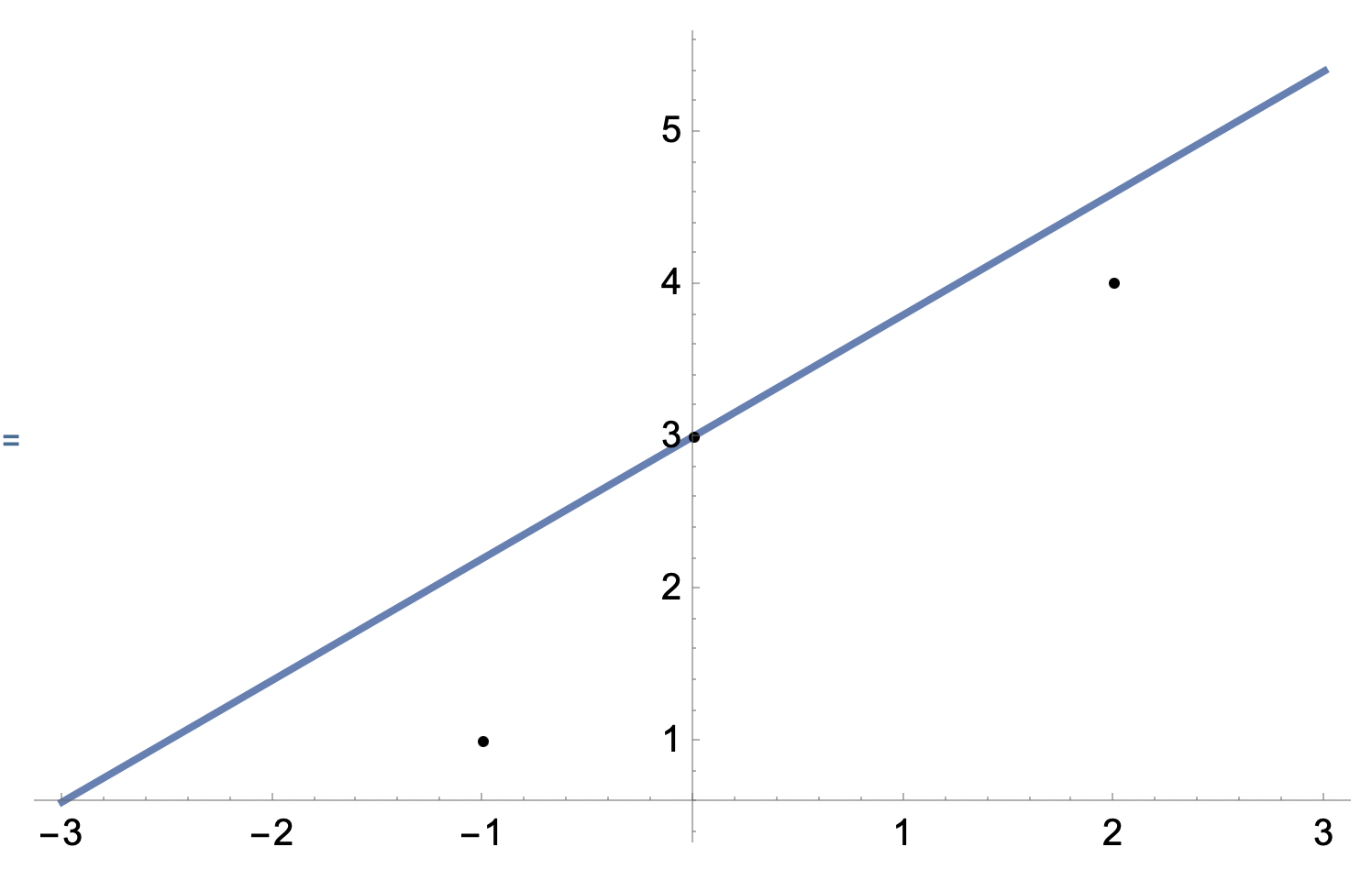
Vad säger facit?

Trinity2 skrev:

OskarT skrev:

Uppgift:

Vi vill göra en anpassning med en rät linje till de tre punkterna (x1, y1) = (−1, 1), (x2, y2) = (0, 3) och (x3, y3) = (2, 4).

Vi antar nu att de tre punkterna är mätdata där den andra punkten är betydligt mer noggrant bestämd än de båda övriga punkterna. Bestäm den räta linje y = kx + m som passerar genom punkten (x2, y2) och anpassar till de båda andra punkterna i minstakvadratmening.


Hur långt jag har kommit:

Jag har kommit fram till att en linje som anpassar sig till alla tre punkter utan att gå genom (x2, y2) har ekvationen $y = \frac{13x}{14} + \frac{33}{14}$. Vet ej hur jag ska göra vidare.

Jag skulle tro att de vill att du skall minimera avstånden enl. minsta kvadratmetoden.

Jag får y=4/5 x+3

Vad säger facit?

Facit säger samma som du fick men hur ska man få fram det?

OskarT skrev:

Trinity2 skrev:

Visa föregående citat

OskarT skrev:

Uppgift:

Vi vill göra en anpassning med en rät linje till de tre punkterna (x1, y1) = (−1, 1), (x2, y2) = (0, 3) och (x3, y3) = (2, 4).

Vi antar nu att de tre punkterna är mätdata där den andra punkten är betydligt mer noggrant bestämd än de båda övriga punkterna. Bestäm den räta linje y = kx + m som passerar genom punkten (x2, y2) och anpassar till de båda andra punkterna i minstakvadratmening.


Hur långt jag har kommit:

Jag har kommit fram till att en linje som anpassar sig till alla tre punkter utan att gå genom (x2, y2) har ekvationen $y = \frac{13x}{14} + \frac{33}{14}$. Vet ej hur jag ska göra vidare.

Jag skulle tro att de vill att du skall minimera avstånden enl. minsta kvadratmetoden.

Jag får y=4/5 x+3

Vad säger facit?

Facit säger samma som du fick men hur ska man få fram det?

Jag löste det analytiskt. Jag skall fundera lite på en lin.alg.metod. Jag vill minnas A^tAx=A^ty där det gäller att välja matriserna lämpligt. Återkommer, om inte någon lin-alg-expert griper in tidigare....

Jag är rätt kass på linjär algebra, men kan ju ge mig på en klassisk lösning som fungerar helt OK för detta problem.

Förhoppningsvis visar den hur minstakvadratmetoden fungerar.

Vi börjar med en rät linje genom (0, 3) eftersom uppgiften kräver det:

$y=kx+3$

Sedan tecknar vi uttryck för felet (residualen) för var punkt:

residual=(linjens y-värde) - (mätvärdet)

Punkten (-1, 1):

$r_1=k\times (-1)+3-1=-k+2$

Punkten (0,3):

Den här skippar vi, eftersom vi vet att felet är noll.

Punkten (2, 4):

$r_3=k\times 2+3-4=2k-1$

Sedan summerar vi kvadraten av felen:

$S\left(k\right)={r_1^2+r_3^2=(-k+2)}^2+{(2k-1)}^2=k^2+4-4k+4k^2+1-4k=5k^2-8k-5$

Nu vill vi minimera S givet k, så först deriverar vi:

$S\text{'}\left(k\right)=10k-8$

Därefter sätter vi derivatan till noll och löser för k:

$$\begin{gathered} 0=10k-8 \\ 10k=8 \\ k=\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$10$}\right.=\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$5$}\right. \end{gathered}$$

Vi har alltså en extrempunkt vid k=4/5. (Denna är ett minimum eftersom koefficienten framför k² är positiv.)

Din anpassade linje är alltså: $\boxed{y=\frac{4}{5}x+3}$

Jag gjorde först som sictransit men jag är lite tvkesam om det är lin.alg.vägen. Men den funkar!

Jag skulle gissa på att lin.alg.metoden är som följer. LuMa07 et al får rätta mig, då de vet mkt bättre.

Vi vet att vi vill ha en passning, i någon mening, av y=kx+3 och vi har 2 punker som skall bestämma k.

4=2k+3

1=-k+3

Detta är överbestämt och vi får göra en m.k.-anpassning. 

Vi skriver det matris-form (och här blir det rörigt då detta är en "skrivmaskin")

{4,1}^T = { {2,1}, {-1,1} } {x,3}^T

där T = transponatet

VL kallar vi Y, 2x2-matrisen i HL kallar vi A och 2x1 matrisen längst till höger kallar vi X

Vi kan nu, i MK-mening, beräkna X genom

A^T AX = A^T Y 

vilket ger ekvationerna

3+5k=7

6+k=5

Den sista ekvationen kan vi förkasta, då vi tvingat l=3 och vi har alltså

3+5k=7 eller k=4/5.

Detta skulle jag gissa på är "lin.alg.-metoden", men slugare personer får gärna rätta om det är fel.