Ansätt homogena ekvationen Asin(2x)+Bcos(2x) istället för Ce^(rx)
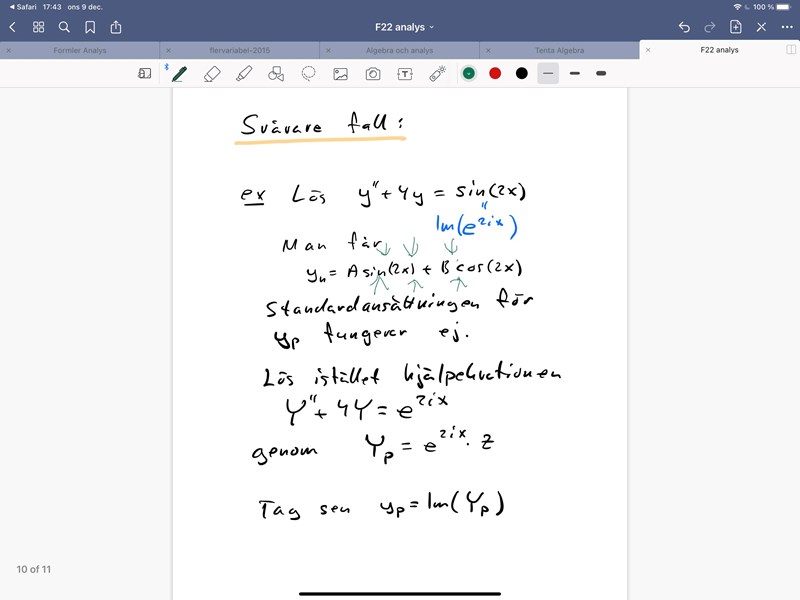 Känns ju ganska rimligt att man ska ansätta en trig. homogen lösning som i exemplet ovan till en trig. diff. ekv. Är det någon som kan utveckla varför man gör det förutom att det är intuitivt. Tack på förhand!
Känns ju ganska rimligt att man ska ansätta en trig. homogen lösning som i exemplet ovan till en trig. diff. ekv. Är det någon som kan utveckla varför man gör det förutom att det är intuitivt. Tack på förhand!
Man ansätter väl en partikulärlösning och räknar ut en homogen lösning i normalfallet? Det är när den karaktäristiska ekvationen, i ditt fall r^2+4=0, har komplexa lösningar som man skriver om de till sin och cos från det e^i... man får.
Jag skulle vilja utveckla det en smula. Du börjar alltid med att lösa , vilket blir .
Inhomogena fallet: Den traditionella ansatsen fungerar inte, eftersom denna inhomogena ansats redan är homogena lösningar. I stället löser vi det inhomogena fallet med den komplexa metoden. Ansätt altså .
Märker att jag var otydlig med över vad jag var förvirrad över. Det jag var förvirrad över var varför man skulle ansätta en trigonometrisk homogen lösning och inte ansätta en Ce^(rx) homogen lösning som man gör ofta annars.
Hej,
Den homogena lösningen ansätts aldrig utan räknas fram; det är partikulärlösningen som ansätts och dess koefficienter matchas mot randvillkor.



