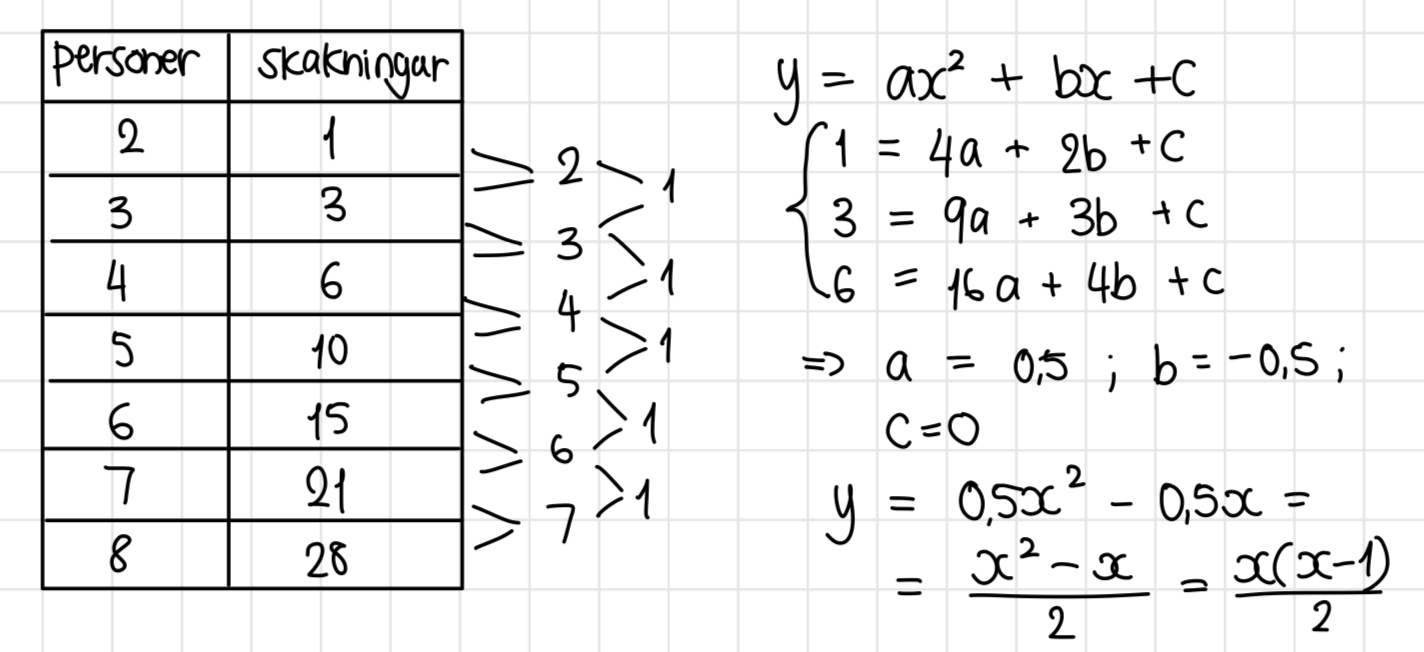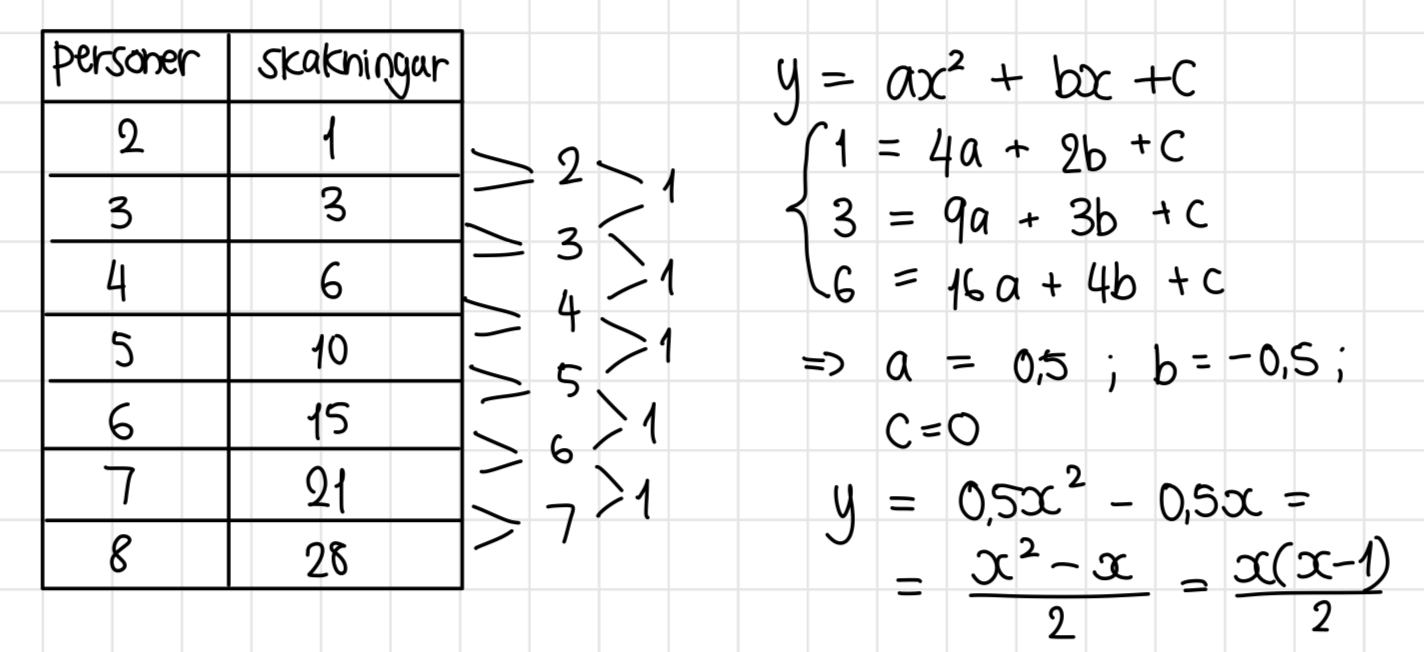Antal handskakningar mellan n personer
Hej! Jag behöver lite hjälp med att komma fram till svaret på ett annat sätt. Den är på C nivå och digitala verktyg är inte tillåtna, men jag har både använt digitala verktyg och lagt ner mer arbete än vad som krävs för en C-uppgift (enligt mig).
"Hur många handskakningar krävs det som minst för att alla ska skaka hand med alla i ett sällskap om sällskapet består av n personer?"
Jag började med att skriva upp hur många handskakningar det skulle vara mellan 2, 3, 4, 5 personer osv. Då fick jag summorna: 1, 3, 6, 10, 15, 21, 28...
Jag ser att mellan varje tal i talföljden ökar det med 2, 3, 4, 5, 6, 7...
Ett sätt jag kan tänka mig lösa det är genom att skriva upp ett ekvationssystem. Genom att lösa ekvationssystemet mha digitala verktyg får jag funktionen .
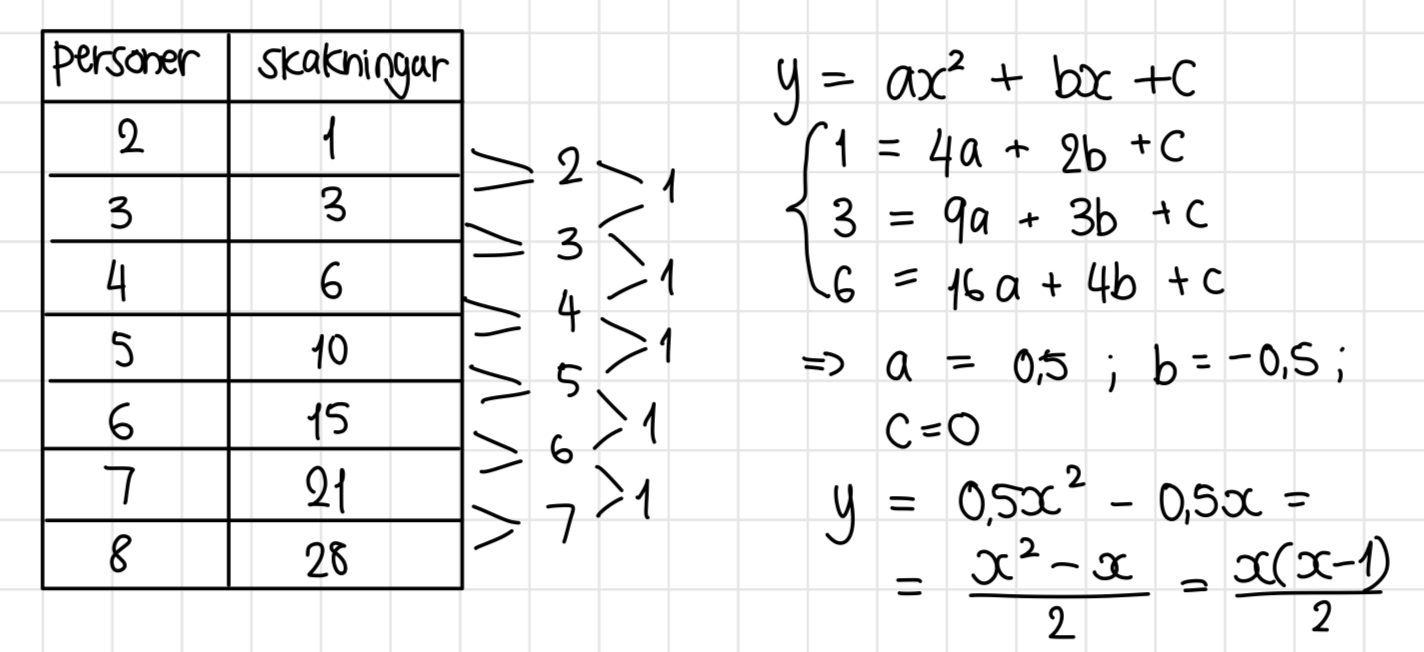
Jag tolkar det som att det finns x sätt att välja person 1 och (x-1) sätt att välja person 2, sen så är det delat på 2 för att varje person skakar med varandra 2 gånger.
Det som jag inte förstår är varför man tar x(x-1), skulle det inte bara fungera för person 1 och 2? och inte för de följande personerna?
Finns det något annat sätt att lösa uppgiften? Det passar inte in på aritmetisk summa eller geometrisk summa, men finns det någon annan metod eller "formel" man skulle kunna applicera för att lösa det?
Tacksam för hjälp!
katie5 skrev:Hej! Jag behöver lite hjälp med att komma fram till svaret på ett annat sätt. Den är på C nivå och digitala verktyg är inte tillåtna, men jag har både använt digitala verktyg och lagt ner mer arbete än vad som krävs för en C-uppgift (enligt mig).
"Hur många handskakningar krävs det som minst för att alla ska skaka hand med alla i ett sällskap om sällskapet består av n personer?"
Jag började med att skriva upp hur många handskakningar det skulle vara mellan 2, 3, 4, 5 personer osv. Då fick jag summorna: 1, 3, 6, 10, 15, 21, 28...
Jag ser att mellan varje tal i talföljden ökar det med 2, 3, 4, 5, 6, 7...
Ett sätt jag kan tänka mig lösa det är genom att skriva upp ett ekvationssystem. Genom att lösa ekvationssystemet mha digitala verktyg får jag funktionen .
Jag tolkar det som att det finns x sätt att välja person 1 och (x-1) sätt att välja person 2, sen så är det delat på 2 för att varje person skakar med varandra 2 gånger.
Det som jag inte förstår är varför man tar x(x-1), skulle det inte bara fungera för person 1 och 2? och inte för de följande personerna?
Finns det något annat sätt att lösa uppgiften? Det passar inte in på aritmetisk summa eller geometrisk summa, men finns det någon annan metod eller "formel" man skulle kunna applicera för att lösa det?
Tacksam för hjälp!
Detta är ett vanligt förekommande problem och det finns många sätt att lösa det på. Det du har gjort är ett bra sätt.
Din direkta fråga, som jag tolkar det är varför det är x(x-1)/2 och inte x(x-1). Det beror på att
a) EN godtycklig person kan inte skaka hand med sig själv (det räknas iaf inte som en handskaning) utan skakar hand med x-1 andra. Så VARJE person framkallar x-1 handskakningar och då det är x personer blir det totalt x(x-1) handskakningar, men då vi löper igenom alla personer 1, 2, 3, ..., x kommer vi att få dubbelt så många handskakningar då vi både räknar när person skakar hand med person 2, som att vi räknar när person 2 skakar hand med person 1 osv. Alltså måste vi dela med 2 och får x(x-1)/2.
b) Använder du kombinatorik är problemet "På hur många sätt kan vi välja 2 olika objekt utan återläggning från en mängd på x objekt". Svaret på det är "x över 2" som är just x(x-1)/2.
c) Ser vi på det som en rekursion låter vi S(x)="Antalet handskaningar vid x personer". S(2)=1. Utgå sedan från en grupp på x-1 personer. För denna grupp är antalet handskakningar S(x-1). Lägg nu till en person till gruppen (då består den av x personer). Denna nytillkomne skall skaka hand med x-1 personer så antalet nya handskakningar som tillkommer förutom dom som redan har skett i gruppen på x-1 personer är x-1 och vi har
S(x) = S(x-1) + x-1, S(2)=1
Här kan man räkna fram S(3)=3, S(4)=6 osv. precis som du har gjort. Som du sedan konstaterar blir 2a-differenserna konstant 1 och det visar på att man skall ansätta ett 2a-gradspolynom (där är lite som att säga att andra-derivatan skall vara konstant, vilket den är för 2a-gradspolynom) och lösa det uppkomna ekvationssystemet, vilket du har gjort på rätt sätt.
Trinity2 skrev:katie5 skrev:Hej! Jag behöver lite hjälp med att komma fram till svaret på ett annat sätt. Den är på C nivå och digitala verktyg är inte tillåtna, men jag har både använt digitala verktyg och lagt ner mer arbete än vad som krävs för en C-uppgift (enligt mig).
"Hur många handskakningar krävs det som minst för att alla ska skaka hand med alla i ett sällskap om sällskapet består av n personer?"
Jag började med att skriva upp hur många handskakningar det skulle vara mellan 2, 3, 4, 5 personer osv. Då fick jag summorna: 1, 3, 6, 10, 15, 21, 28...
Jag ser att mellan varje tal i talföljden ökar det med 2, 3, 4, 5, 6, 7...
Ett sätt jag kan tänka mig lösa det är genom att skriva upp ett ekvationssystem. Genom att lösa ekvationssystemet mha digitala verktyg får jag funktionen .
Jag tolkar det som att det finns x sätt att välja person 1 och (x-1) sätt att välja person 2, sen så är det delat på 2 för att varje person skakar med varandra 2 gånger.
Det som jag inte förstår är varför man tar x(x-1), skulle det inte bara fungera för person 1 och 2? och inte för de följande personerna?
Finns det något annat sätt att lösa uppgiften? Det passar inte in på aritmetisk summa eller geometrisk summa, men finns det någon annan metod eller "formel" man skulle kunna applicera för att lösa det?
Tacksam för hjälp!
Detta är ett vanligt förekommande problem och det finns många sätt att lösa det på. Det du har gjort är ett bra sätt.
Din direkta fråga, som jag tolkar det är varför det är x(x-1)/2 och inte x(x-1). Det beror på att
a) EN godtycklig person kan inte skaka hand med sig själv (det räknas iaf inte som en handskaning) utan skakar hand med x-1 andra. Så VARJE person framkallar x-1 handskakningar och då det är x personer blir det totalt x(x-1) handskakningar, men då vi löper igenom alla personer 1, 2, 3, ..., x kommer vi att få dubbelt så många handskakningar då vi både räknar när person skakar hand med person 2, som att vi räknar när person 2 skakar hand med person 1 osv. Alltså måste vi dela med 2 och får x(x-1)/2.
b) Använder du kombinatorik är problemet "På hur många sätt kan vi välja 2 olika objekt utan återläggning från en mängd på x objekt". Svaret på det är "x över 2" som är just x(x-1)/2.
c) Ser vi på det som en rekursion låter vi S(x)="Antalet handskaningar vid x personer". S(2)=1. Utgå sedan från en grupp på x-1 personer. För denna grupp är antalet handskakningar S(x-1). Lägg nu till en person till gruppen (då består den av x personer). Denna nytillkomne skall skaka hand med x-1 personer så antalet nya handskakningar som tillkommer förutom dom som redan har skett i gruppen på x-1 personer är x-1 och vi har
S(x) = S(x-1) + x-1, S(2)=1
Här kan man räkna fram S(3)=3, S(4)=6 osv. precis som du har gjort. Som du sedan konstaterar blir 2a-differenserna konstant 1 och det visar på att man skall ansätta ett 2a-gradspolynom (där är lite som att säga att andra-derivatan skall vara konstant, vilket den är för 2a-gradspolynom) och lösa det uppkomna ekvationssystemet, vilket du har gjort på rätt sätt.
Tack för det tydliga svaret! Hur man löser det med kombinatorik och rekursion gjorde uppgiften mycket lättare att lösa 😊
Mitt sätt att tolka binomialkoefficienten är hur många olika listor av längden man kan göra givet objekt där ordning inte spelar roll. Med den tolkningen tycker jag man lättare inser att svaret bara är . Det är bara ett tips.
Att kunna lösa problem på flera olika sätt är dock optimalt, och jag skulle väl säga att resonera som du gjorde är den säkraste metoden för att inte råka göra ett tankefel. Så bra jobbat!
katie5 skrev:[...]
Finns det något annat sätt att lösa uppgiften?
[...]
Ytterligare ett sätt att lösa uppgiften är följande:
Tänk dig att alla n personerna står i ett rum.
Person 1 skakar hand med alla andra och går sedan ut ur rummet. Det blir n-1 handskakningar.
Person 2 skakar hand med alla kvarvarande och går sedan ut ur rummet. Det blir ytterligare n-2 handskakningar.
Och så vidare, tills det endast är 2 personer kvar i rummet. De skakar hand med varandra och går tillsammans ut ur rummet. Det blir den sista handskakningen.
Alla har nu skakat hand med alla och det totala antalet handskakningar blir 1+2+3+...+(n-1) = [aritmetisk summa] = (n-1)*(1+(n-1))/2 = n(n-1)/2