Antalet lösningar till ekvationssytemet
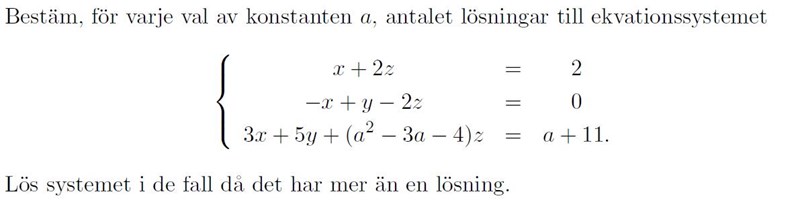
Hej! Börjat lösa uppgiften med att skriva ekvationerna på matrisform. Men vet inte inte hur jag borde gå tillväga efter.
Bra! Undersök nu determinanten. När är den noll? :)
Det verkar lämpligt att börja summera de två översta ekvationerna:
Därefter fås ett ekvationssystem i två variabler: och .
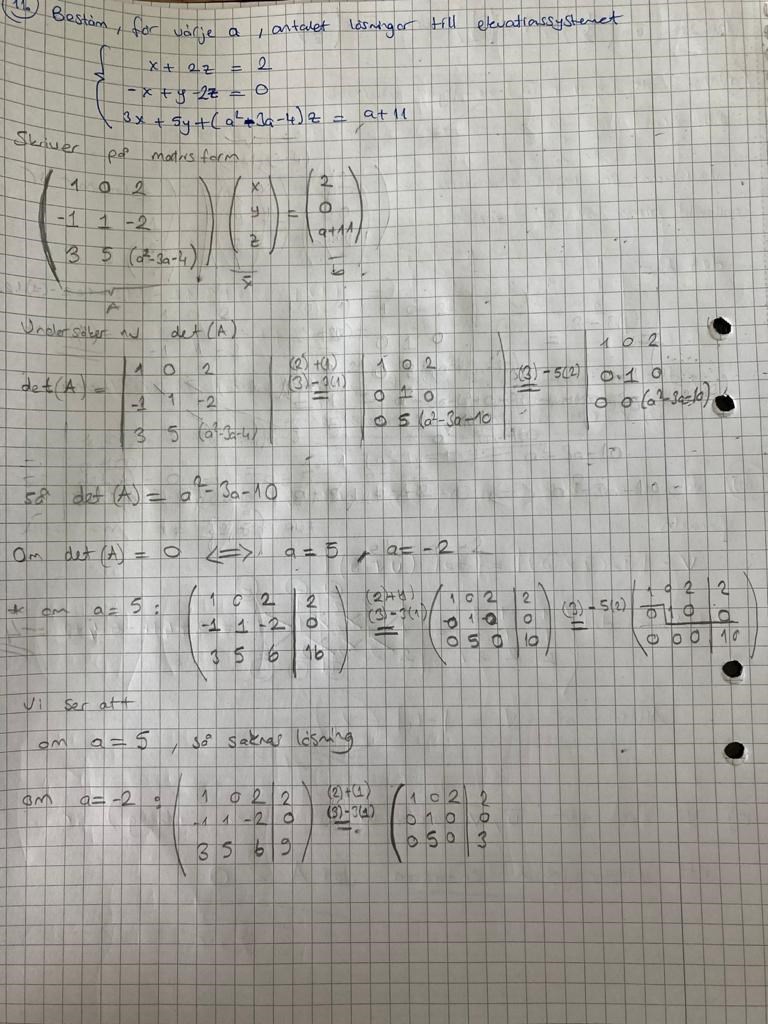
Hej! Jag har undersökt determinanten men vad är nästa steg? I vilka fall har ekvationssystemet mer än en lösning?
Om har ekvationssystemet en unik lösning.
Om har ekvationssystemet antingen ingen eller oändligt många lösningar.
Prova att lösa det för de två värden på som ger .
Jag har kommit fram till att
om a≠5 och -2 så har ekvationssystemet entydig lösning
om a=5 så har ekvationssystemet oändligt många lösningar
om a= -2 så saknas lösning
Stämmer detta? Jag har inte facit och vill bara veta om jag har gjort rätt.
Det verkar stämma.
Tack!



