Antalet lösningar till ett ekvationssystem

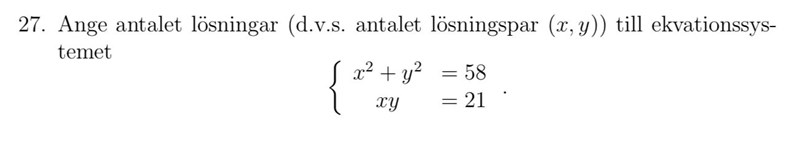
$\begin{array}{r} {(\frac{21}{y})}^{2} + y^{2} = 58 \\ x = \frac{21}{y} \end{array}\} F i n n e r 4 l ö s n i n g a r t i l l d e t h ä r e k v a t i o n s s y s t e m e t, m e d d e h ä r v i l l k o r e n . F a c i t s ä g e r o c k s å a t t d e t f i n n s 4 l ö s n i n g a r . P r o b l e m e t ä r a t t o m m a n g ö r s å h ä r : \begin{array}{r} {(\frac{21}{x})}^{2} + x^{2} = 58 \\ y = \frac{21}{x} \end{array}\} S å f i n n s d e t 4 f l e r l ö s n i n g a r . A l l t s å f i n n s d e t 4 t i l l l ö s n i n g a r t i l l e k v a t i o n e n . R ä k n a s d e t s o m s a m m a l ö s n i n g a r, o c h d ä r f ö r f i n n s d e t b a r a 4 l ö s n i n g a r t i l l e k v a t i o n s s y s t e m e t ?$

Hur hittar du fler än 4 lösningar? Kom ihåg att dina lösningar måste satisfiera båda ekvationerna, dvs även xy = 21 måste vara uppfyllt (x = 7, y = -3 är alltså inte en lösning).

Fann 4 lösningar för den översta omskrivningen av ekvationssystemet, och sedan 4 till (samma fast y är uttryckt i termer av x istället för tvärt om som innan).

Kan du skriva de lösningar du har hittat här i tråden?

Listade bara ut att det fanns 8 lösningar totalt. Inte exakta värde för de. Gjorde såhär:

$\{\begin{cases} {(\frac{21}{y})}^{2} + y^{2} = 58 \\ x = \frac{21}{y} \end{cases} F i n n s e n l ö s n i n g f ö r : 0 \leq y \leq 1 F i n n s e n l ö s n i n g f ö r : y > 1 F i n n s e n l ö s n i n g f ö r : 0 > y > - 1 F i n n s e n l ö s n i n g f ö r : - 1 \geq y S a m m a g ä l l e r f ö r o m m a n u t t r y c k e r y i t e r m e r a v x . A l l t s å f i n n s d e t 8 l ö s n i n g a r$

Här (som så många andra gånger) skulle jag börja med att rita. Har du gjort det?

Jag håller inte med om dina olikheter. För att ta den översta:

Antag att $0 \leq y \leq 1$

Att y=0 och y=1 inte är lösningar ser man lätt genom prövning. Då återstår 0<y<1

Men om 0<y<1 så gäller att $\frac{21}{y} > 21$ och ${(\frac{21}{y})}^{2} > 21^{2} = 441$

Men då gäller även att ${(\frac{21}{y})}^{2} + y^{2} > 441$ , och då ser man att y inte kan finnas i det intervallet!

Tänk ett varv till på problemet, och berätta hur du tänker.

Ok, då finns det två lösningar för när man uttrycker x i termer av y och två lösningar för tvärtom, totalt blir det 4. Tack så mycket för hjälpen!

x=-7, -3, 3, 7

y=-7, -3, 3, 7

Rita, så syns det tydligt! Den övre ekvationen ger en cirkel, den undre blir av typen y=k/x. Graferna kommer att skära varandra i fyra punkter.

Svara

Visa senaste svar