Använda integraler för areaberäknig

Jag skulle gjort på följande sätt:

1. Invertera bägge leden
2. Kvadrera bägge leden
3. Substituera t = x^2 och lös andragradsekvationen.
4. Substituera tillbaka till x.

Ska prova men hur menar du med invertera?

passar på att fråga på fortsättningen. Jag kör fast... (se mederdelen på pappret)

Om man som jag får får x = +/- roten ur 3 - hur ska jag använda detta?

Jag hade löst det såhär, börja att multiplicera båda leden med $1 + x^2$ så får man

$$\begin{gathered} 2=\frac{1+x^2}{\sqrt{1+x^2}}\iff \\ 2=\sqrt{1 + x^2}\iff \\ 4=1+x^2\iff \\ {x}^2=3\iff \\ x=\pm \sqrt{3} \end{gathered}$$

gulfi52 skrev :

Ska prova men hur menar du med invertera?

Jag menar att om VL = HL så är 1/VL = 1/HL.

Detta förutsätter förstås att både VL och HL är skilda från 0, vilket är fallet i detta fallet.

Jg kanske kan lösa skärningen, punkt 2 på pappret, men punkt 1) f(x)-g(x) får jag inte ihop...

Det gäller att

$\int \frac{1}{x^2 + 1} dx = \arctan(x) + C$

Samt att

$\int \frac{1}{\sqrt{1 + x^2}} dx = \sinh^{-1}(x) + C$

Den senare kan man beräkna genom variabelbytet $t = \sinh(x)$ och använda den hyperboliska ettan. Om man känner sig bekväm med de hyperboliska funktionerna dvs.

Hej!

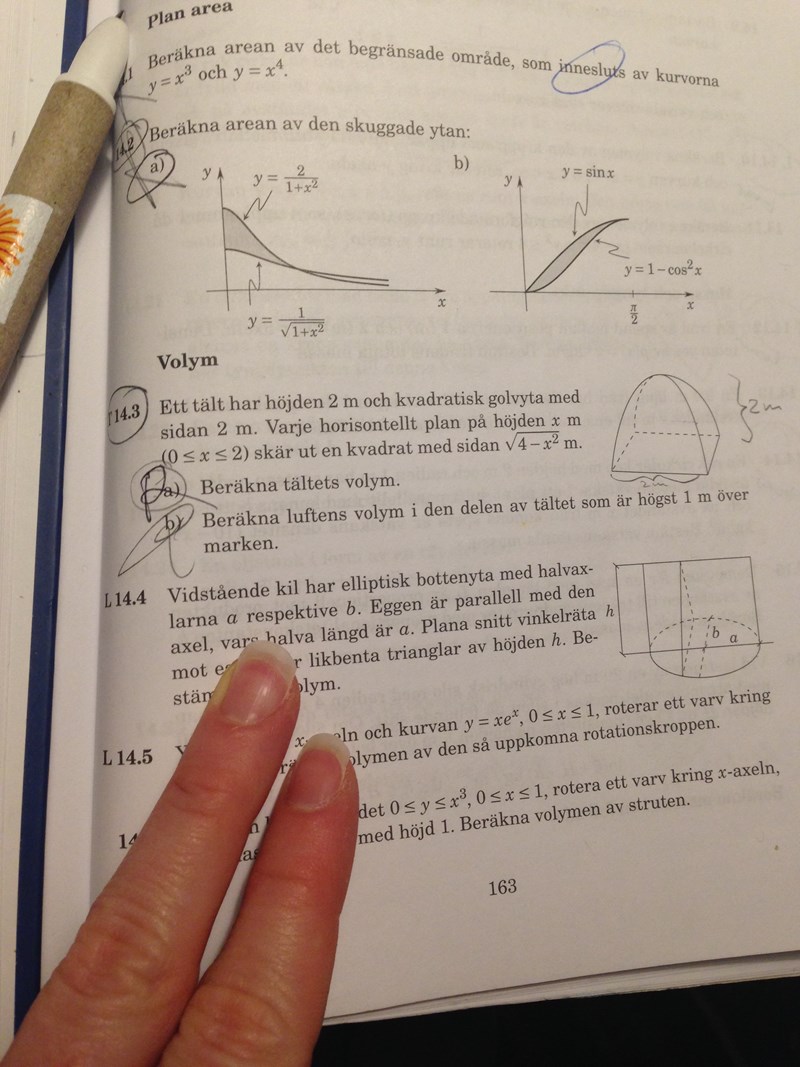
Uppgift 14.2 a: Beräkna arean av den skuggade ytan mellan de två graferna.

Den skuggade ytans area är lika med integralen

    $\int_{0}^{a} \frac{2}{1+x^2}-\frac{1}{\sqrt{1+x^2}}\,\text{d}x\ ,$

där det positiva talet $a$ är sådant att

    $\frac{2}{1+a^2} = \frac{1}{\sqrt{1+a^2}}$

det vill säga $a=\sqrt{3}\ .$

Albiki

Stokastisk skrev :

Det gäller att

$\int \frac{1}{x^2 + 1} dx = \arctan(x) + C$

Samt att

$\int \frac{1}{\sqrt{1 + x^2}} dx = \sinh^{-1}(x) + C$

Den senare kan man beräkna genom variabelbytet $t = \sinh(x)$ och använda den hyperboliska ettan. Om man känner sig bekväm med de hyperboliska funktionerna dvs.

Men... är inte promotiven till den senare av de två 

ln av x+(roten ur (1+x^2) ) ?

Stokastisk skrev :

Jag hade löst det såhär, börja att multiplicera båda leden med $1 + x^2$ så får man

$$\begin{gathered} 2=\frac{1+x^2}{\sqrt{1+x^2}}\iff \\ 2=\sqrt{1 + x^2}\iff \\ 4=1+x^2\iff \\ {x}^2=3\iff \\ x=\pm \sqrt{3} \end{gathered}$$

Hur går du från steg ett till steg två?

Duh, $\sinh^{-1}(x) = \ln(x + \sqrt{1 + x^2})$, är inte det uppenbart :P Nej skämt åsido likheten mellan detta gäller men det kanske inte är uppenbart, man ser det genom att beräkna inversen till $\sinh(x)$ på följande sätt:

$$\begin{gathered} y=\frac{e^x-e^{-x}}{2}\Rightarrow \\ 2e^{x}y=e^{2x}-1\Rightarrow \\ {e}^{2x}-2e^{x}y-1=0\Rightarrow \\ {e}^x=y+\sqrt{y^2+1}\Rightarrow \\ x=\ln (y+\sqrt{y^2+1}) \end{gathered}$$

Så inversen till $\sinh(x)$ är $\ln(x + \sqrt{1 + x^2})$.

För att gå mellan steg 1 och steg 2 så se det som att $a = 1 + x^2$ då står det ju

$2=\frac{a}{\sqrt{a}}$

Eftersom $a/\sqrt{a} = \sqrt{a}$ så gäller det alltså att $\frac{x^2 + 1}{\sqrt{x^2 + 1}} = \sqrt{x^2 + 1}$.

Aha - tack :)

och ytterligare ett aha med ett tack!