Använding av Newtons andra lag

Du har ju redan resultatet!

Tyngdkraften liggande block 23 Kg * 9.82 m/(s^2)

Friktionskraften liggande block 23 Kg * 9.82 m/(s^2) * 0.17 = 38.39 N = Spännkraften i snöret

Tyngdkraften hängande cylinder 19 Kg * 9.82 m/(s^2) = 186.5 N

Blockets friktionskraft räcker inte för att hålla cylindern i position. Anordningen kommer att börja axa och snart gör det BUM!

Men så vad är spännkraften?

Plus är "Tyngdkraften liggande block 23 Kg * 9.82 m/(s^2)" relevant? Jag menar tar inte den tyngdkraften och normalkraften ut varandra så den resulterande kraften på det blocket blir 0?

Tror jag löste den. 

Först räknar jag ut accelerationen; F= mxa -> a= F/m   -> (186.5-38,39)/(23+19) = 3,5m/s^2 

Sen så är dom enda relevanta krafterna Friktionskraften och Tyngdkraften för den hängande cylindern; 

Fs=spännkraft

Så F= mxa -> mg - Fs = ma

Fs = mg-ma = 186.5 - 66.5 = 120N

Stämmer det?

Uppgiften är dålig, det avslöjas inte om friktionstalet gäller för vilofriktion eller glidfriktion. Blocket kommer att glida och axa i alla fall. Men jag är inte längre säker på min tidigare lösning. Det är ju två kroppar som accelererar och påverkar varandra.

------------------

mB - massa blocket 23 Kg

mC - massa cylinder 19 Kg

frikB - 0.17 (anta glidfriktion)

g - 9.82

------------

(mB * g * frikB) - (a * mB) = (mC * g) - (a * mC)

(mB * g * frikB) - (mC * g) = (a * mB) - (a * mC)

g * (mB * frikB - mC) = a * (mB - mC)

a = g * (mB * frikB - mC) / (mB - mC)

(inte färdigt)

Så jag har fel alltså?

Nej, du verkar ha tänkt någorlunda rätt Malle. Så här skulle jag sätta upp problemet (S är spännkraften i snöret), $m_1$ är 23kg, $m_2$ är 19kg, frilagda kroppar, Newton 2 (ma=F):

$m_1\ddot x=S-\mu mg$
$m_2\ddot y=m_2g-S$

Eftersom accelerationen är lika för båda kropparna $a=\ddot y= \ddot x$ blir (sätta a=a och lös ut S)

$S=\frac{m_1 m_2 g(1+\mu)}{m_1+m_2}$

Okej men hur kommer det sig att jag ska använda 2 olika newtons andra lag ekvationer och sätta ihop dom? Samt jag förstår inte hur och varför du sätter upp formeln som du gör. Kanske är jag som är lite seg bara men skulle uppskatta om du ville förklara varför du tar m1xm2xgx(1-friktionstalet) 

Jag frilägger varje kropp för sig. Båda kropparna känner av samma kraft (S) från snöret. Båda kropparna accelererar med accelerationen a (den ena åt höger, den andra nedåt). Så här:

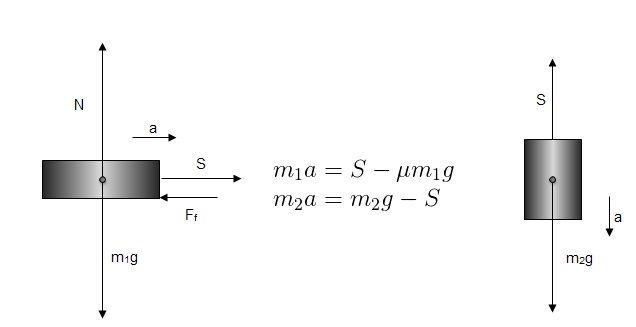
Nu har du alltså två ekvationer och två okända (a och S), använd valfri metod för att lösa ut S. Själv delar jag med $m_1$ respektive $m_2$ och låter a=a ge mig en ekvation för S.

$S=\frac{m_1m_2g(1+\mu)}{m_1+m_2}\approx 120N$

Notera också att du tänkte (ungefär) rätt själv när du räknade ut a. Cylindermassans tyngd ska accelerera båda massorna. Detta är bara en alternativ och mer strikt lösningsgång.

Edit: Uppdaterade $m_1$ med en normalkraft N, $F_f=\mu N=\mu mg$

Okej tack så hemskt mycket för hjälpen, då förstår jag! Men jag fick ju också fram svaret 120N när jag räknade ut den. Var det av ren slump eller går det att lösa talet så också? För jag menar när båda massorna har samma acceleration så borde väl min teknik fungera?

I efterhand verkar Malles lösning vara rätt, bara dåligt förklarad. Guggles lösning är mycket bra. Min ekvation var mindre bra och jag hade ont om tid i förrgår :-(