Är alla trianglar liksidiga?
Jo men jag funderar på om alla trianglar är liksidiga. Jo, jag vet, det låter som en lite korkad fråga men jag har ett ganska övertygande bevis för att så är fallet.
Vi börjar med att kika på en fin bild
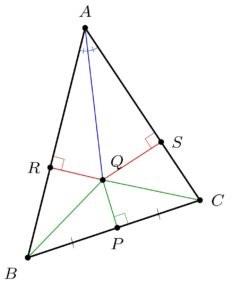
Här har vi en triangel. AQ är bisektris till vinkeln vid A. P är mittpunkt på sträckan BC och PQ är följaktligen mittpunktsnormalen till BC. Q är alltså skärningspunkten mellan bisektrisen vid A och motstående sidas mittpunktsnormal. QR och QS är höjderna i trianglarna AQB respektive AQC.
Trianglarna PQB och PQC är förstås kongruenta så |BQ|=|QC|.
Vidare: de rätvinkliga trianglarna AQR och AQS har alla vinklar lika och kanten AQ gemensam så de är också kongruenta. Det följer att |QR|=|QS| och |AR|=|AS|.
Betrakta nu trianglarna QRB samt QSC. De är rätvinkliga och |QR|=|QS| samt |BQ|=|QC| så även de tredje sidorna är lika, det vill säga: |RB|=|SC|.
Men nu har vi |AR|=|AS| och |RB|=|SC| så |AB|=|AC|.
Alltså är två godtyckliga sidor i en triangel lika långa och alltså är alla trianglar liksidiga.
Är det någon som tror att det här beviset möjligtvis inte stämmer?
Du måste bevisa att punkten där bisektriserna skär varandra och punkten där mittpunktsnormalerna skär varandra är densamma. Lycka till med det!
Hej!
Liksidiga??!!!! Menar du likbenta?
"Betrakta nu trianglarna QRB samt QSC. De är rätvinkliga och |QR|=|QS| samt |BQ|=|QC| så även de tredje sidorna är lika, det vill säga: |RB|=|SC|. "
Stämmer inte för att
Om det är två sidor som är lika långa och två vinklar lika stora betyder nödvändigtvis inte att trianglarna är kongruenta, så länge de vinklarna ligger inte mellan de två liklånga sidorna.
Om du kollar på trianglarna QSC och QRB så är QS=QB och QC=QB och för att att de här två trianglarna ska vara kongruenra så måsta vinklarna CQS och BQR vara lika stora, för att de här två vinklarna ligger mellan de två lika långa sidorna.
Mvh
Smaragdalena skrev:Du måste bevisa att punkten där bisektriserna skär varandra och punkten där mittpunktsnormalerna skär varandra är densamma. Lycka till med det!
Nä det måste jag väl inte bevisa? Ingenstans i beviset har jag antagit det.
Q är alltså skärningen mellan bisektrisen från A och mittpunktsnormalen till BC. Det har inget att göra med punkten där bisektriserna skär varandra eller punkten där mittpunktsnormalerna skär varandra.
Mohammad Abdalla skrev:Hej!
Liksidiga??!!!! Menar du likbenta?
"Betrakta nu trianglarna QRB samt QSC. De är rätvinkliga och |QR|=|QS| samt |BQ|=|QC| så även de tredje sidorna är lika, det vill säga: |RB|=|SC|. "
Stämmer inte för att
Om det är två sidor som är lika långa och två vinklar lika stora betyder nödvändigtvis inte att trianglarna är kongruenta, så länge de vinklarna ligger inte mellan de två liklånga sidorna.
Om du kollar på trianglarna QSC och QRB så är QS=QB och QC=QB och för att att de här två trianglarna ska vara kongruenra så måsta vinklarna CQS och BQR vara lika stora, för att de här två vinklarna ligger mellan de två lika långa sidorna.
Mvh
Du bortser ifrån att det är rätvinkliga trianglar. Om hypotenusorna i två rätvinkliga trianglar är lika och en katet är lika i de två trianglarna är den andra kateten given av Pythagoras sats. I trianglarna QSC och QRB är hypotenusorna QB och QC lika och en katet är lika, dvs QS=QR. Pythagoras sats ger då att även den andra kateten är lika, dvs RB = SC.
Och för att vara övertydlig: jag vet att beviset är felaktigt, förstås, och jag vet var felet ligger. Kluringen är att finna felet och helst att förklara lite varför det är fel.
Lite bakgrund om problemet: det falska beviset är påhittar av Charles Dodgson mer känd som Lewis Caroll. Syftet är att illustrera hur lätt vi luras av vår egen geometriska intutition.
Det finns alltså ett specifikt steg i beviset som är felaktigt. Hitta det!
Smutsmunnen skrev:Smaragdalena skrev:Du måste bevisa att punkten där bisektriserna skär varandra och punkten där mittpunktsnormalerna skär varandra är densamma. Lycka till med det!
Nä det måste jag väl inte bevisa? Ingenstans i beviset har jag antagit det.
Q är alltså skärningen mellan bisektrisen från A och mittpunktsnormalen till BC. Det har inget att göra med punkten där bisektriserna skär varandra eller punkten där mittpunktsnormalerna skär varandra.
Då formulerar jag det annorlunda: Du måste bevis att de tre Q-punkterna sammanfaller. Det är precis samma sak osm jag skrev tidigare. Du påstår ju att det finns EN punkt Q, eftersom du använder den till flera trianglar.
Smaragdalena skrev:Smutsmunnen skrev:Smaragdalena skrev:Du måste bevisa att punkten där bisektriserna skär varandra och punkten där mittpunktsnormalerna skär varandra är densamma. Lycka till med det!
Nä det måste jag väl inte bevisa? Ingenstans i beviset har jag antagit det.
Q är alltså skärningen mellan bisektrisen från A och mittpunktsnormalen till BC. Det har inget att göra med punkten där bisektriserna skär varandra eller punkten där mittpunktsnormalerna skär varandra.
Då formulerar jag det annorlunda: Du måste bevis att de tre Q-punkterna sammanfaller. Det är precis samma sak osm jag skrev tidigare. Du påstår ju att det finns EN punkt Q, eftersom du använder den till flera trianglar.
Jag använder väl bara en Q. Skärningen mellan bisektrisen från A och mittpunktsnormalen till BC. Linjerna BQ och QC antar jag inte vara bisektriser och linjerna QR och QS antar jag inte vara mittpunktsnormaler. Så du har missförstått något.
Hej!
Felet är att man antar att bisektrisen möter mittpunktsnormalen inuti triangeln. De möts utanför triangln.
Mvh
Mohammad Abdalla skrev:Hej!
Felet är att man antar att bisektrisen möter mittpunktsnormalen inuti triangeln. De möts utanför triangln.
Mvh
Hej nu börjar det likna något.
Du har rätt att de möts utanför triangeln och att min möjligtvis missledande figur får det att se ut som att de möts innanför triangeln men varför gör det beviset felaktigt? Utnyttjar beviset att de möts innanför?
Jag smäller upp en till figur:
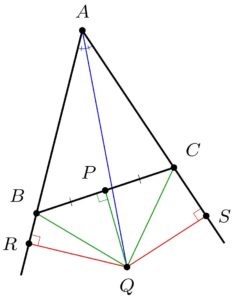
Nu kan vi göra beviset exakt som ovan förutom sista steget:
det vill säga vi har |AR|=|AS| och |BR|=|SC| så slutsatsen |AB|=|AC| följer ändå men med subtraktion istället för addition.
Smutsmunnen skrev:Mohammad Abdalla skrev:Hej!
Felet är att man antar att bisektrisen möter mittpunktsnormalen inuti triangeln. De möts utanför triangln.
Mvh
Hej nu börjar det likna något.
Du har rätt att de möts utanför triangeln och att min möjligtvis missledande figur får det att se ut som att de möts innanför triangeln men varför gör det beviset felaktigt? Utnyttjar beviset att de möts innanför?
Jag smäller upp en till figur:
Nu kan vi göra beviset exakt som ovan förutom sista steget:
det vill säga vi har |AR|=|AS| och |BR|=|SC| så slutsatsen |AB|=|AC| följer ändå men med subtraktion istället för addition.
Det här beviset stämmer inte heller.
Smutsmunnen skrev:Mohammad Abdalla skrev:Hej!
Felet är att man antar att bisektrisen möter mittpunktsnormalen inuti triangeln. De möts utanför triangln.
Mvh
Hej nu börjar det likna något.
Du har rätt att de möts utanför triangeln och att min möjligtvis missledande figur får det att se ut som att de möts innanför triangeln men varför gör det beviset felaktigt? Utnyttjar beviset att de möts innanför?
Jag smäller upp en till figur:
Nu kan vi göra beviset exakt som ovan förutom sista steget:
det vill säga vi har |AR|=|AS| och |BR|=|SC| så slutsatsen |AB|=|AC| följer ändå men med subtraktion istället för addition.
Men du skriver att |BR| = |SC| !!! Det gäller ju bara om det är en liksidig triangel, dvs om P ligger på |AQ|. Du påstår alltså saker som förutsätter att det är en liksidig triangel och med det bevisar du att det är en liksidig triangel...
Om det nu vore en liksidig triangel skulle du dessutom kunna sätta din punkt P var som helst på |AQ|.
bengali skrev:Smutsmunnen skrev:Mohammad Abdalla skrev:Hej!
Felet är att man antar att bisektrisen möter mittpunktsnormalen inuti triangeln. De möts utanför triangln.
Mvh
Hej nu börjar det likna något.
Du har rätt att de möts utanför triangeln och att min möjligtvis missledande figur får det att se ut som att de möts innanför triangeln men varför gör det beviset felaktigt? Utnyttjar beviset att de möts innanför?
Jag smäller upp en till figur:
Nu kan vi göra beviset exakt som ovan förutom sista steget:
det vill säga vi har |AR|=|AS| och |BR|=|SC| så slutsatsen |AB|=|AC| följer ändå men med subtraktion istället för addition.
Men du skriver att |BR| = |SC| !!! Det gäller ju bara om det är en liksidig triangel, dvs om P ligger på |AQ|. Du påstår alltså saker som förutsätter att det är en liksidig triangel och med det bevisar du att det är en liksidig triangel...
Om det nu vore en liksidig triangel skulle du dessutom kunna sätta din punkt P var som helst på |AQ|.
Nej att |BR|=|SC| bevisar jag i den ursprungliga posten. Det gäller också på riktigt i alla trianglar, så det är inte där felet i beviset ligger. Ingen aning varför du tror att det bara gäller i liksidiga trianglar.
Du har å andra sidan rätt att om triangeln vore liksidig eller likbent så skulle jag kunna sätta punkten Q var som helst på |AP| men det är ju inget problem. Beviset görs under antagande att |AB| är skilt ifrån |AC| vilket visar sig leda till motsägelse. Om |AB|=|AC| så är inte punkten Q entydigt definierad men det spelar ingen roll, det är inte en egenskap hos liksidiga trianglar vi vill härleda, utan att bevisa att det inte existerar andra än liksidiga trianglar.
Jag kan förövrigt rent allmänt säga att felet i beviset inte beror på cirkularitet, felet är ett rent felslut.
Lite mer om punkten Q: Q:s läge kan beskrivas mycket precist, på riktigt alltså, inte i låtsas beviset, Q ligger på triangelns omskrivna cirkel, precis där cirkelbågen mellan B och C delas mitt i tu.
Smutsmunnen skrev:Jag kan förövrigt rent allmänt säga att felet i beviset inte beror på cirkularitet, felet är ett rent felslut.
Lite mer om punkten Q: Q:s läge kan beskrivas mycket precist, på riktigt alltså, inte i låtsas beviset, Q ligger på triangelns omskrivna cirkel, precis där cirkelbågen mellan B och C delas mitt i tu.
Felet i andra bilden är att R måste ligga mellan A och B.
Mohammad Abdalla skrev:Smutsmunnen skrev:Jag kan förövrigt rent allmänt säga att felet i beviset inte beror på cirkularitet, felet är ett rent felslut.
Lite mer om punkten Q: Q:s läge kan beskrivas mycket precist, på riktigt alltså, inte i låtsas beviset, Q ligger på triangelns omskrivna cirkel, precis där cirkelbågen mellan B och C delas mitt i tu.
Felet i andra bilden är att R måste ligga mellan A och B.
Äntligen! Där kom det rätta svaret.
Mer precis: punkterna A,B och R ligger inte i samma ordning som punkterna A,C och S. Om R ligger mellan A och B så ligger S inte mellan A och C och vice versa.
Därför är det sista steget i beviset felaktigt, allting fram tills dess är korrekt: dvs
|AR|=|AS| och |RB|=|SC|
men |AB|=|AR|+|RB|
medan |AC|=|AS|-|SC| eller vice versa.
Jag vet inte, det känns inte som att folk tyckte det här var lika roligt som jag tyckte.
I vilket fall: Dodgson poäng var att begreppet ordning nästan alltid utelämnas i framställningar av elementär Euklidisk geometri, mattelärare säger nästan aldrig sådant som " punkterna A,B,C ligger i samma ordning som punkterna D,E,F" utan vi förlitar oss nästan helt på figurer för det. Lite bedrägliga figurer och konstiga saker tycks följa...
Smutsmunnen skrev:Mohammad Abdalla skrev:Smutsmunnen skrev:Jag kan förövrigt rent allmänt säga att felet i beviset inte beror på cirkularitet, felet är ett rent felslut.
Lite mer om punkten Q: Q:s läge kan beskrivas mycket precist, på riktigt alltså, inte i låtsas beviset, Q ligger på triangelns omskrivna cirkel, precis där cirkelbågen mellan B och C delas mitt i tu.
Felet i andra bilden är att R måste ligga mellan A och B.
Äntligen! Där kom det rätta svaret.
Mer precis: punkterna A,B och R ligger inte i samma ordning som punkterna A,C och S. Om R ligger mellan A och B så ligger S inte mellan A och C och vice versa.
Därför är det sista steget i beviset felaktigt, allting fram tills dess är korrekt: dvs
|AR|=|AS| och |RB|=|SC|
men |AB|=|AR|+|RB|
medan |AC|=|AS|-|SB| eller vice versa.
Jag vet inte, det känns inte som att folk tyckte det här var lika roligt som jag tyckte.
I vilket fall: Dodgson poäng var att begreppet ordning nästan alltid utelämnas i framställningar av elementär Euklidisk geometri, mattelärare säger nästan aldrig sådant som " punkterna A,B,C ligger i samma ordning som punkterna D,E,F" utan vi förlitar oss nästan helt på figurer för det. Lite bedrägliga figurer och konstiga saker tycks följa...
Det var väldigt intressant faktiskt. Tack så mycket.



