Är detta nonsens eller inte nonsens?
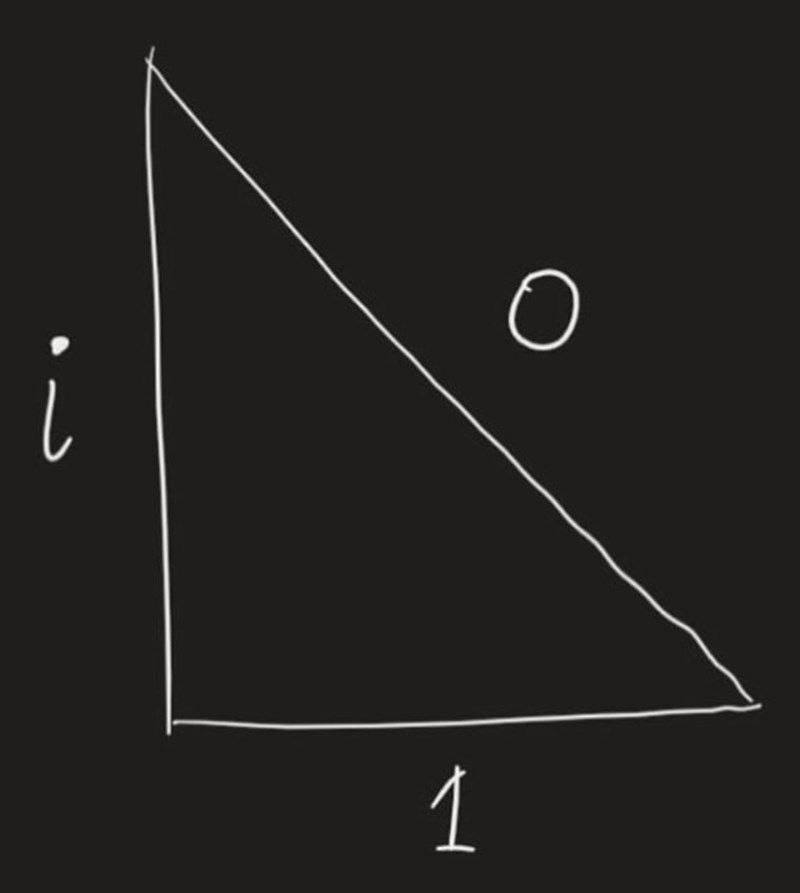
(Den är rätviklig)
Känslan när jag såg det där:
Allt i mig vill säga nonsens. Det skulle kunna gå att konstruera en triangelaktig sak i det komplexa talplanet, men det innebär inte att hypotenusan har längden noll. Talet i ligger ju i det komplexa talplanet och där har talet längden ett, även om det går in i det komplexa talplanet.
Inte nonsens. Hypotenusan o, kateten i och kateten 1.
Om man bortser allt det "konstiga", så stämmer det visserligen att ("pythagoras sats") .
Å andra sidan ser jag detta på 2 "möjliga" sätt.
Det första vore att vi ser dessa som tal i . Vi utgår från origo och ritar ut i och 1. Sedan drar vi då en linje mellan dessa och får då triangeln. Men sen ser vi att detta blir väldigt konstigt då normen av i och 1 är 1 (som tal i ), men normen av 0 är 0.
Det andra sättet är att helt enkelt se i, 1 och 0 som längderna i triangeln. Men då tycker jag återigen att det genast blir problem, eftersom hur vill du ordna talen då vi har komplexa tal? Är i>1? är 2i<7? är 0>i? är 2+3i<10? Hur kan då en längd som vi är vana vid vara ett imaginärt tal som i?
Jag tycker det verkar som nonsens.
Att se det som en triangel i C hjälper inte för hypotenusan blir ju rot2 ändå eller? Jag tänker att den har hörn i origo, i+0 och 1i+0. Som pepparkvarn sa
Finns det ingen teknikalitet kring pythagoras sats som gör att den endast gäller R?
En avståndsfunktion ska ju vara reellvärd. Det är svårt att tolka en komplexvärd avståndsfunktion.





