Är Z och V rågrannar med varandra, matematiskt?
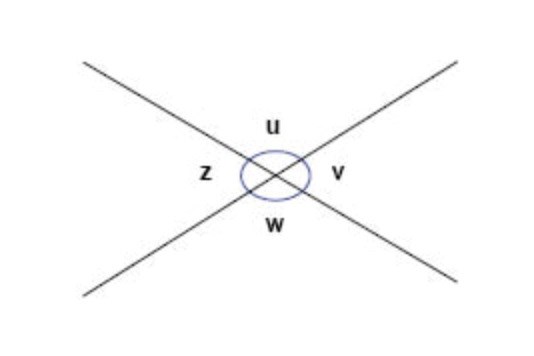
I nedan exempel är det fyra fastighetsgränser. Fastigheterna är z, u, w och v enligt nedan, strecken är fastighetsgränser. Är z då i kontakt med v? Så kallad rågranne, dvs gemensam tomt- eller fastighetsgräns. Med rågranne menas då alltså angränsande fastighet såsom nedan fastighet;
z till u och w,
u till v och z,
v till w och u samt
w till z och v.
Men är då fastighet z och v rågrannar med varandra? Respektive fastighet u och w. Ja eller nej? Och hur förklarar man det matematiskt?
Definitionen för ”rågranne” är inte uttömmande nog. Precist blir det först när man besvarat frågan: Räcker det med att två ”fastigheter” (mängder) har en randpunkt gemensam för att de ska vara rågrannar eller måste hela randen vara gemensam? Det är exakt den frågan jag upplever att du ställer. Någon allmäntopologisk definition för den aktuella situationen har jag aldrig sett. Den är kanske inte intressant nog. Notera också att de ritade fastigheterna är obegränsade ”utåt”, så där saknas randpunkter.
Man skulle kunna tänka sig att cirkeln består av fyra bågar och att två fastighetsbågar är rågrannar omm de har en gemensam punkt.
Båge z och båge v saknar gemensam punkt.

