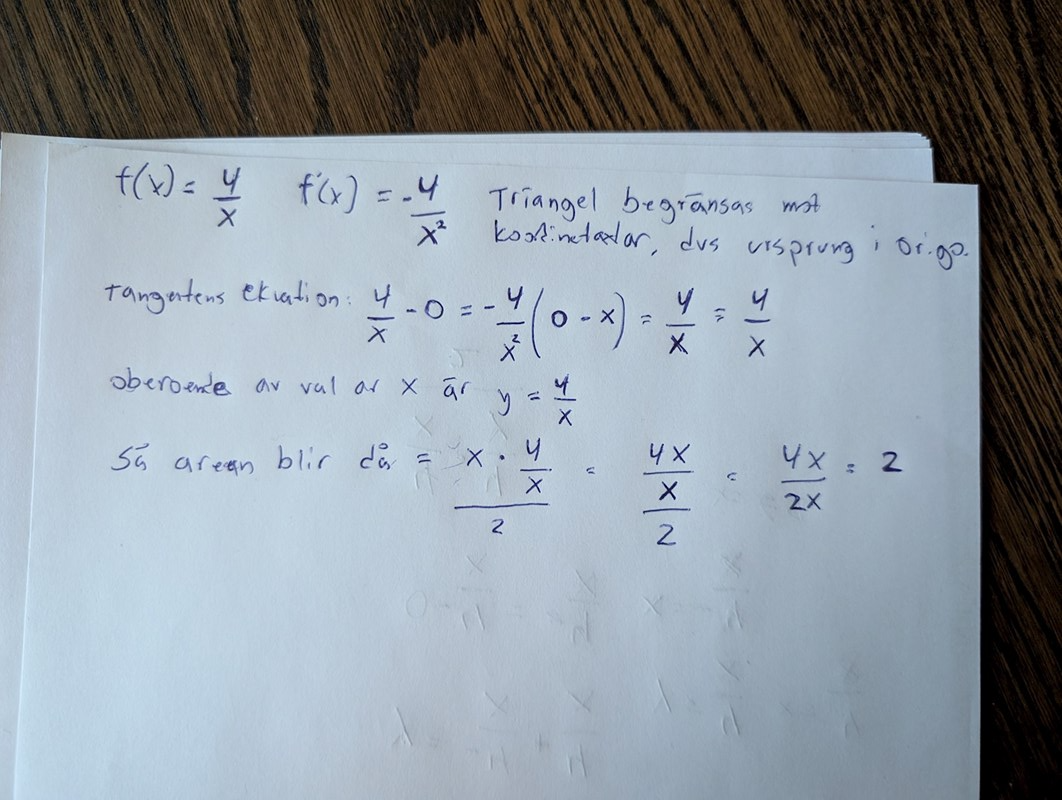Area av triangel oberoende av valet av p

Har du ritat en skiss med kurvan och en tangent vid en godtycklig punkt P?

Om inte, gör det.

Inför lämpliga obekanta storheter i skissen och använd dessa för att sätta upp ett uttryck för triangelns area.

Visa din skiss och dina uttryck.

Såhär har jag gjort 

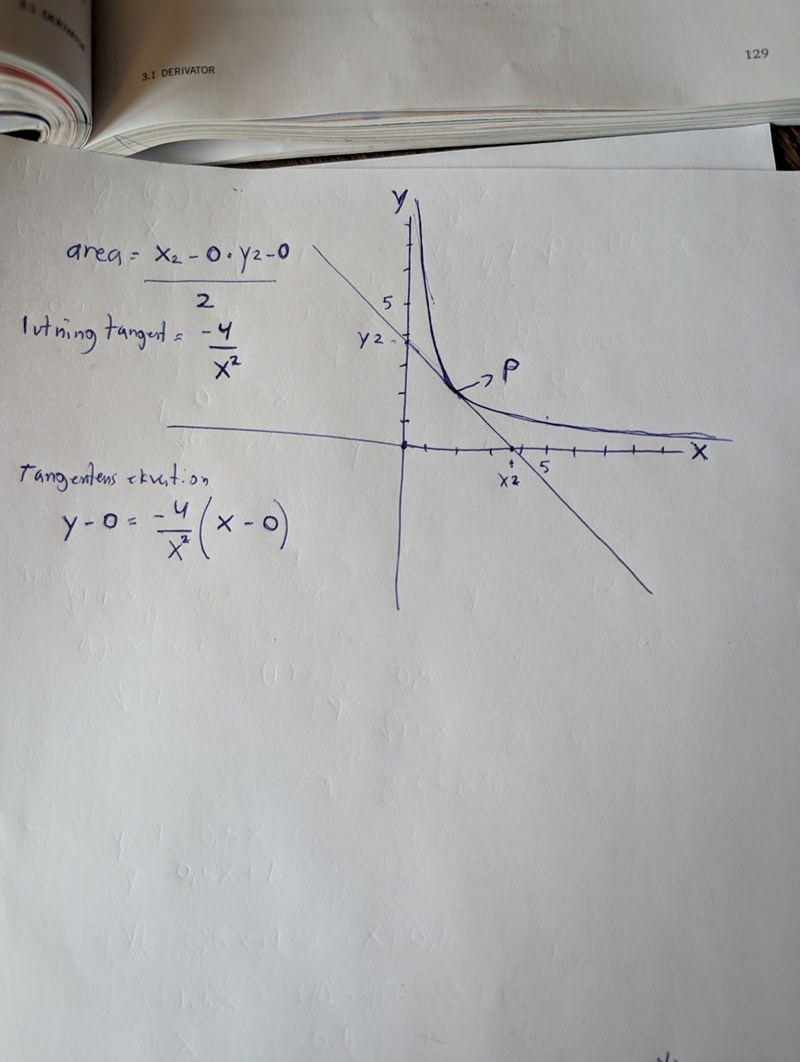
Kompletterad:

Fast nej, det har inget med saken att göra tror jag 

Jag får att triangelns area alltid kommer att vara= -2, men jag antar att det ska vara 2 här så måste ha glömt att vända tecken någonstans..

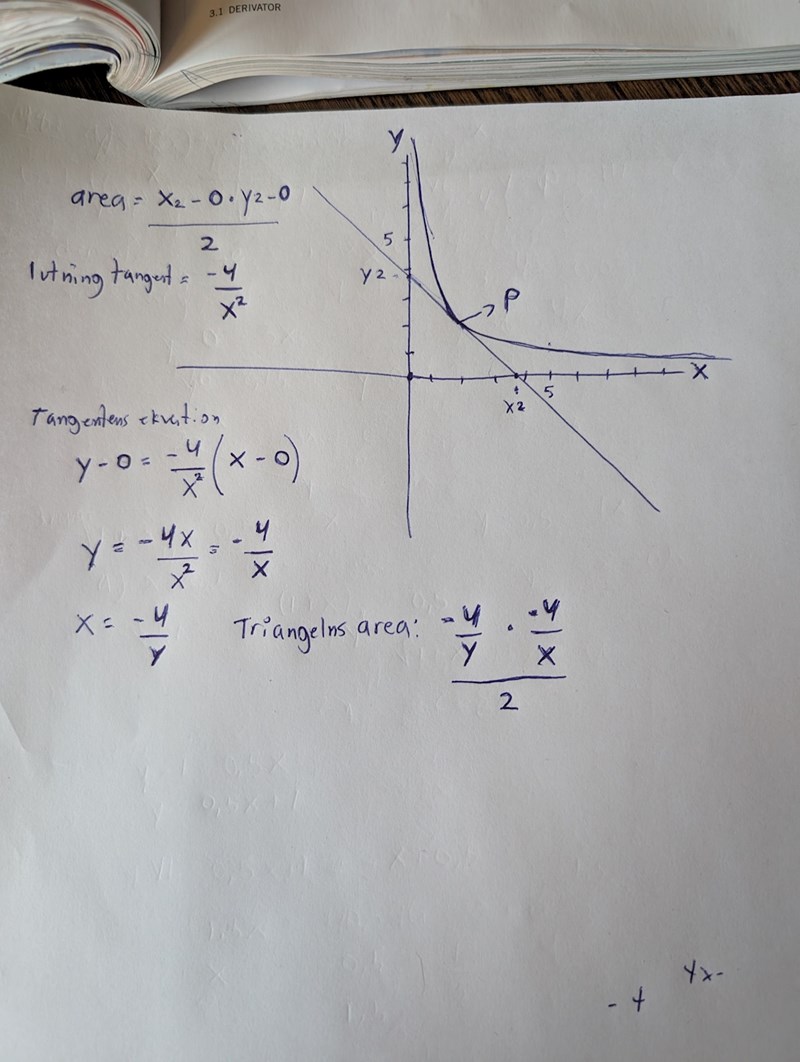
Såhär:

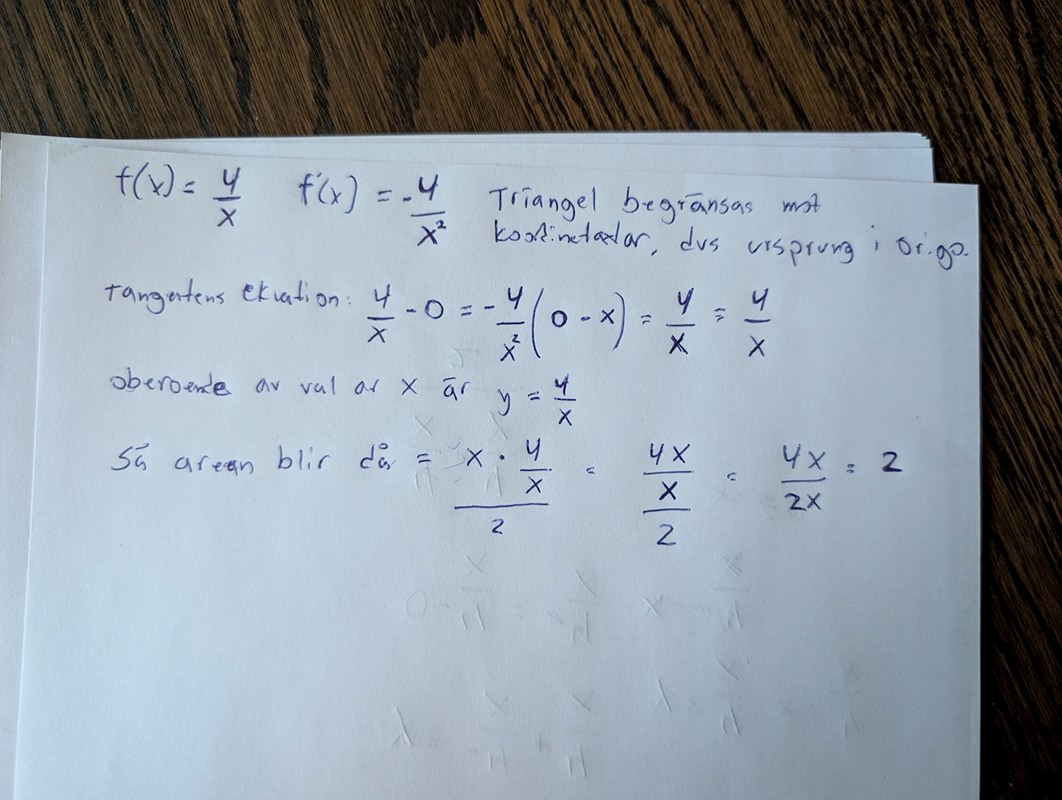
Dkcre skrev:

Såhär:

Snyggt.

Tack!

Stämmer det att triangelns area är 2 ae (jag får 8 ae)?
Det är otydligt vilken ekvation du anser att tangenten har.
Och vad x och y står för på olika ställen.
Kanske jag som har svårt att hänga med, men lösningen kan nog göras tydligare.

Tänkte precis skriva! Nej, det är fel. Svaret är 8 a.e.

Men jag har gjort mitt bästa, ingen aning hur man kommer fram till det.

Om P = (a, 4/a) blir tangentens ekvation y = - 4x/a² + m,

där insättning av P ger m = 8/a (tangentens skärning med y-axeln).

y = 0 ger x =2a (tangentens skärning med x-axeln)

Area 2a *(8/a)/2 = 8

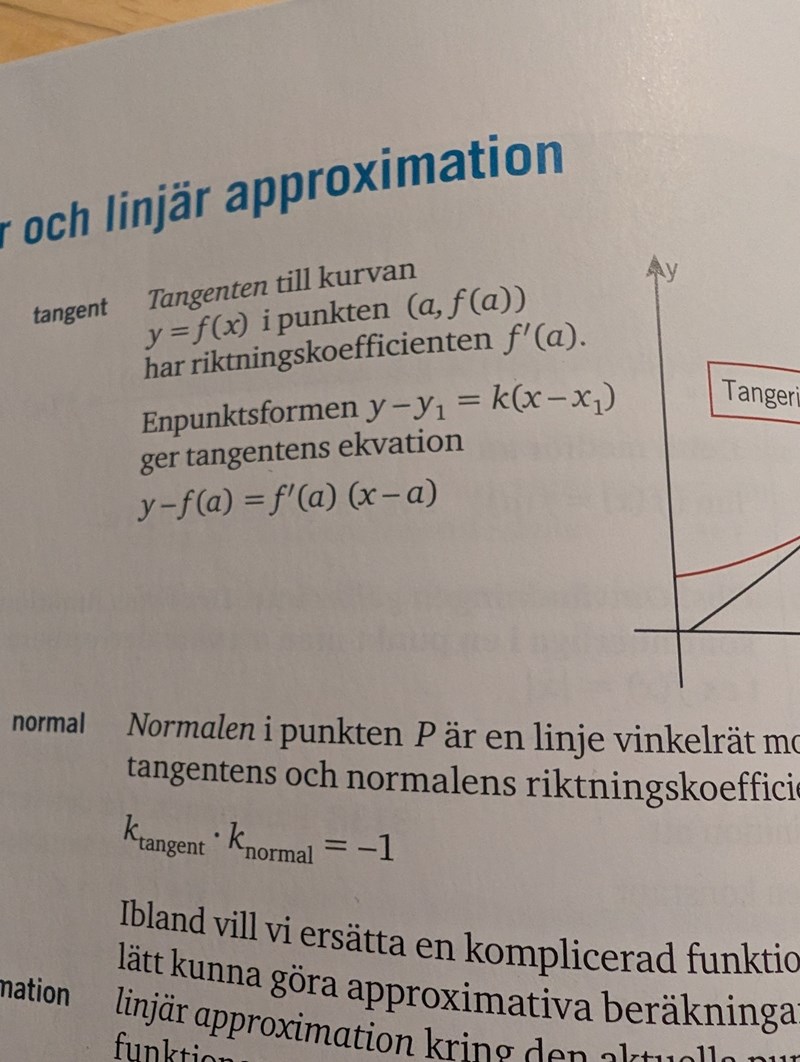
Det ser ut som du vill använda enpunktsformeln. Bra idé.

Du har k redan, samt punkten P. Säg att den har koordinaterna P=(a, 4/a).

Ja, vad jag ser Louis precis skrivit ... :-)

Okej, det hade jag aldrig klarat tyvärr.

Insättning av p där menar du att man sätter x = 0 också då?

I tangentens ekvation y = - 4x/a² + m sätter du in P, dvs x=a och y= 4/a.

Det ger m = 8/a så att ekvationen blir y = - 4x/a² + 8/a.

Okej tack 

Oj, där svarade jag utan att läsa ordentligt. Ber om ursäkt för det.

Hur kommer man fram till tangentens ekvation? Försökte själv nu men det går inte.

Jag kommer fram till det här, lite annat än y = -(4x/a^2) + m

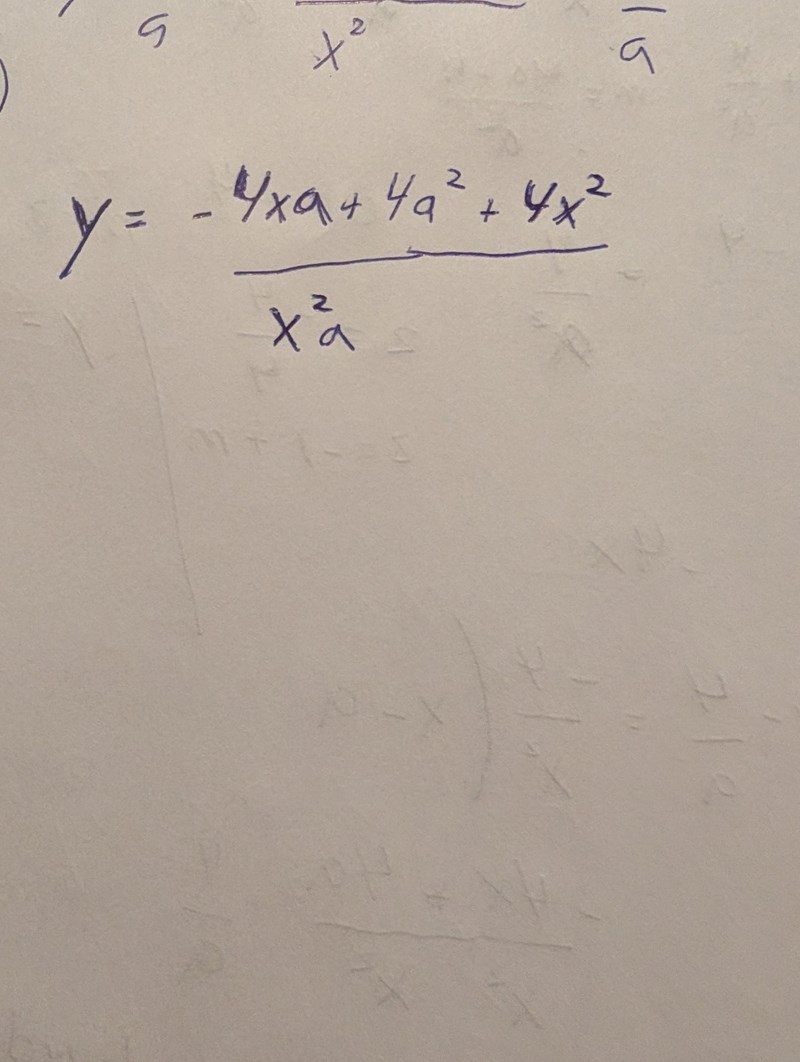
Hur kom du fram till det?

Tangenten är en rät linje som alltså kan skrivas på formen y = kx + m.

k är kurvans lutning i tangeringspunkten där x = a.

Då y'(x) = -4/x²  blir  k= y'(a) = -4/a².

I boken här står det hur man ska göra, jag följde det bara så blir det så.

Och ja.. just det. Måste lära mig att a och x där är två olika saker.. tycker att det är samma. Har haft svårt för det sen matte 1.

Okej då, nu blev det något annat :3

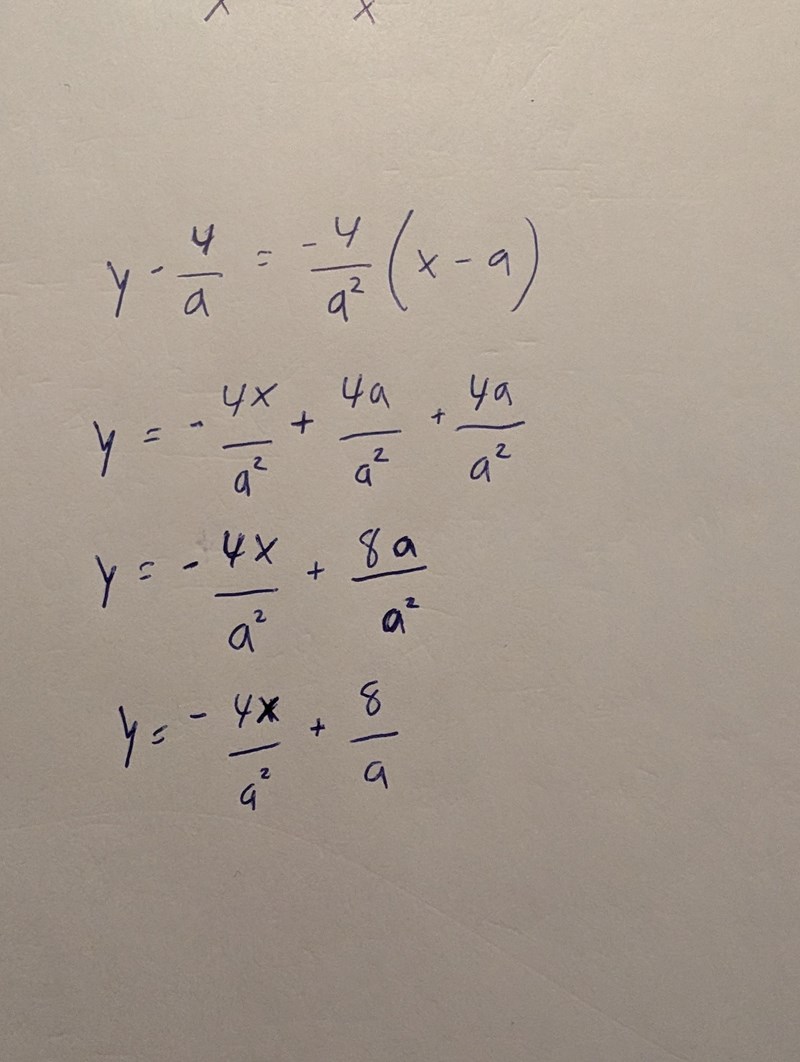
Ja, nu är det rätt. Enpunktsformen fungerar minst lika bra som att gå via beräkning av m.

Är du med på hur den fungerar?

Jadå, tror det 🙂 tack