Area med nya variabler
Hej!
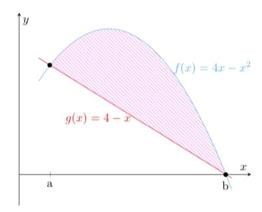
Beräkna den efterfrågade arean genom att införa ett nytt koordinatsystem med t-axeln genom linjen och vinkelrät mot .
Därefter, beräkna arean som:
Det verkar inte ha hänt så mycket här, har du lust att dela med dig av din lösning?
Vad jag kan se går det inte att skapa en sådan funktion , eftersom för flera -värden finns två -värden.

(Bilden i ursprungsinlägget har olika skalor på axlarna, vilket gör att det ser ut att vara möjligt, men i själva verket är det inte det.)
Tack Moffen för att du väckte min tråd till liv! Jag ger lite tips på vägen så kanske någon fyller i resten? ✊️
Sätt:
Detta ger:
AlvinB skrev:Vad jag kan se går det inte att skapa en sådan funktion , eftersom för flera -värden finns två -värden.
(Bilden i ursprungsinlägget har olika skalor på axlarna, vilket gör att det ser ut att vara möjligt, men i själva verket är det inte det.)
Bra poäng, men det räcker att funktionen för är definierad i intervallet .
är avståndet mellan funktionerna och mätt vinkelrätt mot linjen .
tomast80 skrev:AlvinB skrev:[...]
Bra poäng, men det räcker att funktionen för är definierad i intervallet .
Jag hänger inte med. Jag tänker mig att jag roterar och flyttar koordinatsystemet så att linjen hamnar på den horisontella axeln. Då är ju den sökta arean området ovanför den horisontella axeln, men detta avgränsas till vänster av en kurva som inte är en funktion, eller?

Min poäng är helt enkelt att det inte går att för varje punkt längs -axeln få ett unikt avstånd mätt vinkelrätt från -axeln:

Bra poäng, AlvinB, man får räkna ut den mindre arean längst till vänster där det finns dubbla u-värden separat. Min uppgiftsformulering var ej fullständig. Tack för påpekandet! 🙏
tomast80 skrev:Bra poäng, AlvinB, man får räkna ut den mindre arean längst till vänster där det finns dubbla u-värden separat. Min uppgiftsformulering var ej fullständig. Tack för påpekandet! 🙏
Jag måste dock säga att jag gillar idén till problemet, så det är synd att skrota det. Kanske vi kan rädda det genom att välja linjen så att den skär parabeln mellan symmetrilinjen och , t.ex. med linjen ?

Då uppstår inte samma problem.
Jättebra idé AlvinB, vi omformulerar uppgiften enligt ditt förslag ovan! 👏🤝



