Area och likformighet
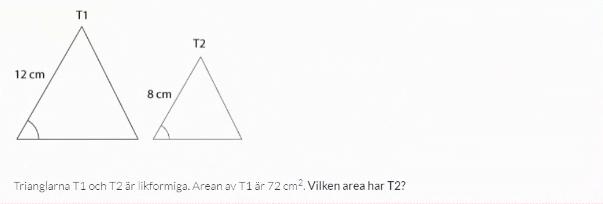
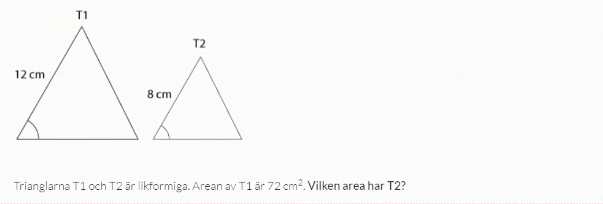
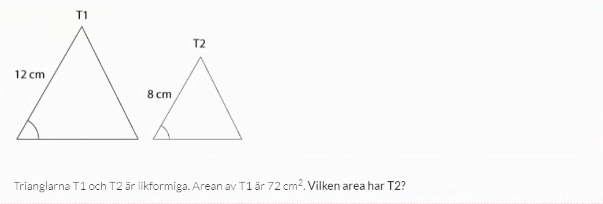
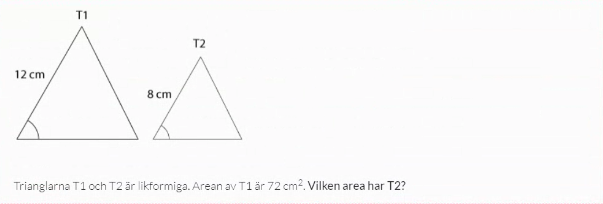
Hur skulle ni ha löst uppgiften nedan?
Jag vet vad förhållandet är mellan sidorna i respektive triangel, men kommer inte längre än så. Testade pythagoras sats men jag har för många variabler. Testade även att multiplicera 72*2, men då får man 72*2=bh, fortfarande två variabler.
OmarTaleb skrev:Hur skulle ni ha löst uppgiften nedan?
Jag vet vad förhållandet är mellan sidorna i respektive triangel, men kommer inte längre än så. Testade pythagoras sats men jag har för många variabler. Testade även att multiplicera 72*2, men då får man 72*2=bh, fortfarande två variabler.
Jag skulle ha kladdat på pappret och fyllt båda trianglarna med mindre trianglar med sidan 4. Det blir 9 trianglar i den vänstra trianglen och 4 i den högra. Om 9 små trianglar har arean 72 så har varje liten triangel arean 72/9 = 8 och 4 små trianglar har arean 4.8 = 32 kvadratcentimeter.
Smaragdalena skrev:OmarTaleb skrev:Hur skulle ni ha löst uppgiften nedan?
Jag vet vad förhållandet är mellan sidorna i respektive triangel, men kommer inte längre än så. Testade pythagoras sats men jag har för många variabler. Testade även att multiplicera 72*2, men då får man 72*2=bh, fortfarande två variabler.
Jag skulle ha kladdat på pappret och fyllt båda trianglarna med mindre trianglar med sidan 4. Det blir 9 trianglar i den vänstra trianglen och 4 i den högra. Om 9 små trianglar har arean 72 så har varje liten triangel arean 72/9 = 8 och 4 små trianglar har arean 4.8 = 32 kvadratcentimeter.
Finns det ingen mer matematisk metod?
Vi får ut arean av en triangel genom att ta b*h/2.
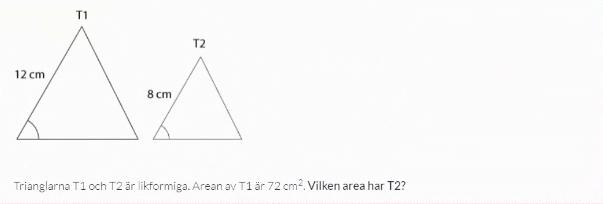
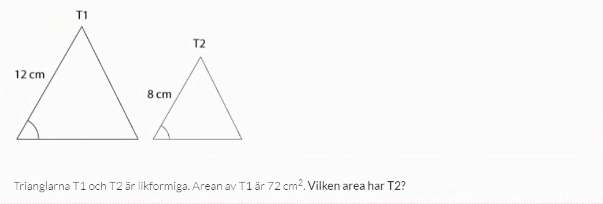
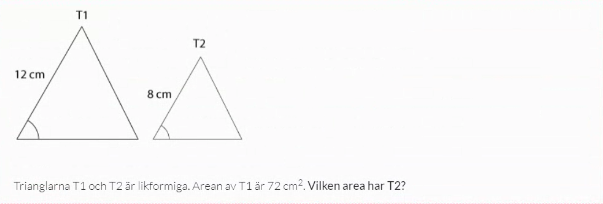
Då vi gör det på T1 får vi 72 cm2.
En sträcka i T1 förhåller sig till en sträcka i T2 som 12:8.
Basen och höjden i T2 är alltså (8/12)*b och (8/12)*h, så arean av T2 ges av [(8/12)*b]*[(8/12)*h]/2 = (8/12)2*b*h/2 = (8/12)2*72.
Finns det ingen mer matematisk metod?
På högskoleprovet är det tidseffektivitet som gäller. Åtminstone för mig skulle det som jag beskrev vara den snabbaste, och därför bästa, metoden.
Smaragdalena skrev:OmarTaleb skrev:Hur skulle ni ha löst uppgiften nedan?
Jag vet vad förhållandet är mellan sidorna i respektive triangel, men kommer inte längre än så. Testade pythagoras sats men jag har för många variabler. Testade även att multiplicera 72*2, men då får man 72*2=bh, fortfarande två variabler.
Jag skulle ha kladdat på pappret och fyllt båda trianglarna med mindre trianglar med sidan 4. Det blir 9 trianglar i den vänstra trianglen och 4 i den högra. Om 9 små trianglar har arean 72 så har varje liten triangel arean 72/9 = 8 och 4 små trianglar har arean 4.8 = 32 kvadratcentimeter.
Betyder likformigheten att alla sidor är samma förhållande? dvs samma 3 vinklar också?
Japp! Lika stora vinklar, och varje sida i figur ett förhåller sig till motsvarande sida i figur två, på samma sätt. :)
eddberlu skrev:Smaragdalena skrev:OmarTaleb skrev:Hur skulle ni ha löst uppgiften nedan?
Jag vet vad förhållandet är mellan sidorna i respektive triangel, men kommer inte längre än så. Testade pythagoras sats men jag har för många variabler. Testade även att multiplicera 72*2, men då får man 72*2=bh, fortfarande två variabler.
Jag skulle ha kladdat på pappret och fyllt båda trianglarna med mindre trianglar med sidan 4. Det blir 9 trianglar i den vänstra trianglen och 4 i den högra. Om 9 små trianglar har arean 72 så har varje liten triangel arean 72/9 = 8 och 4 små trianglar har arean 4.8 = 32 kvadratcentimeter.
Betyder likformigheten att alla sidor är samma förhållande? dvs samma 3 vinklar också?
Ja!
Smaragdalena skrev:OmarTaleb skrev:Hur skulle ni ha löst uppgiften nedan?
Jag vet vad förhållandet är mellan sidorna i respektive triangel, men kommer inte längre än så. Testade pythagoras sats men jag har för många variabler. Testade även att multiplicera 72*2, men då får man 72*2=bh, fortfarande två variabler.
Jag skulle ha kladdat på pappret och fyllt båda trianglarna med mindre trianglar med sidan 4. Det blir 9 trianglar i den vänstra trianglen och 4 i den högra. Om 9 små trianglar har arean 72 så har varje liten triangel arean 72/9 = 8 och 4 små trianglar har arean 4.8 = 32 kvadratcentimeter.
Hur vet du att du ska ta sidan 4? Bara pga 3•4=12?
eddberlu skrev:Smaragdalena skrev:OmarTaleb skrev:Hur skulle ni ha löst uppgiften nedan?
Jag vet vad förhållandet är mellan sidorna i respektive triangel, men kommer inte längre än så. Testade pythagoras sats men jag har för många variabler. Testade även att multiplicera 72*2, men då får man 72*2=bh, fortfarande två variabler.
Jag skulle ha kladdat på pappret och fyllt båda trianglarna med mindre trianglar med sidan 4. Det blir 9 trianglar i den vänstra trianglen och 4 i den högra. Om 9 små trianglar har arean 72 så har varje liten triangel arean 72/9 = 8 och 4 små trianglar har arean 4.8 = 32 kvadratcentimeter.
Hur vet du att du ska ta sidan 4? Bara pga 3•4=12?
Jag är inte Smaragdalena, men troligtvis pga att 12 och 8 båda utgör en multipel av 4.
Ett enkelt sätt är att titta på längd och areaskalan.
Areaskalan ändras med kvadraten på längdskalan, Alltså
Arean för den lilla = (8/12)2*72 = (2/3)2*72 = 4*72/9 = 32