Area trianglar
Jag ska visa att de gråa trianglarna har samma area. Jag har lyckats komma fram till att nedre vänstra triangel är samma area som den i mitten. Jag vet om areasatsen men jag vet inte vinklarna vilket just nu sätter stopp för mig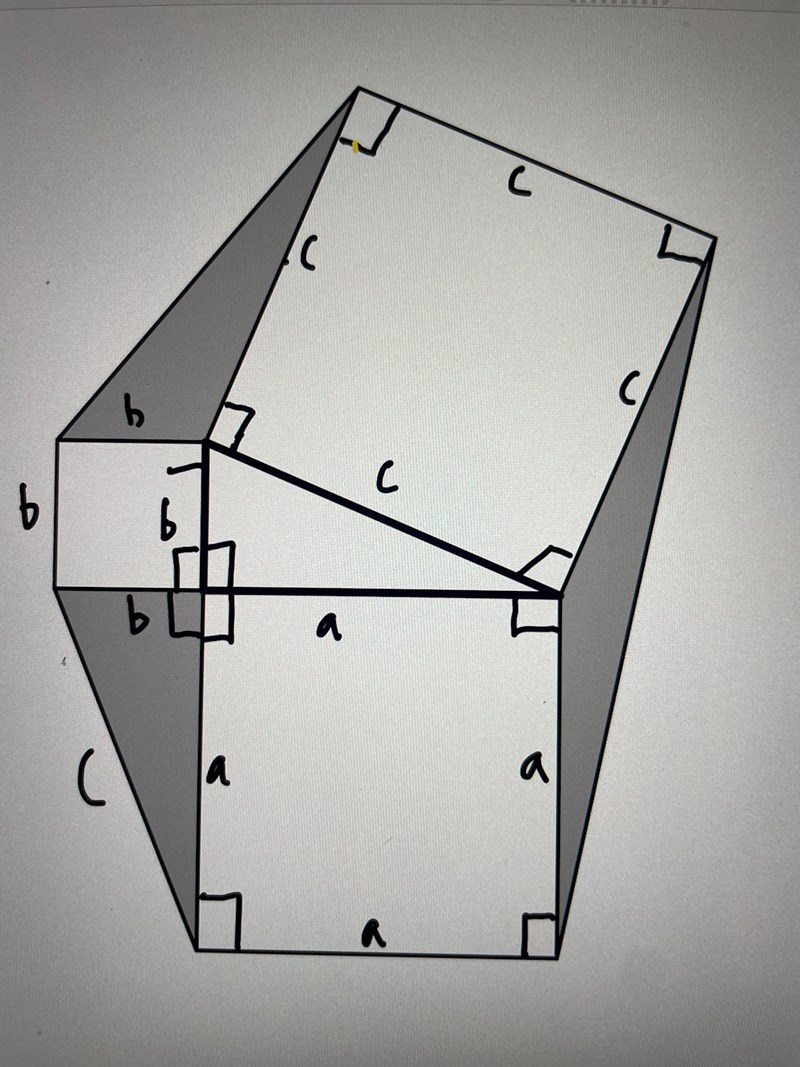
Om du får använda trigonometri:
Definiera A, B, och C som rätvinkliga triangelns interna vinklar. (A är motstående sidan med längd a osv)
Definiera A', B', och C' som trubbiga vinkeln i den skuggade trianeln som delar hörn med A,B,C-vinklarna.
Se figur
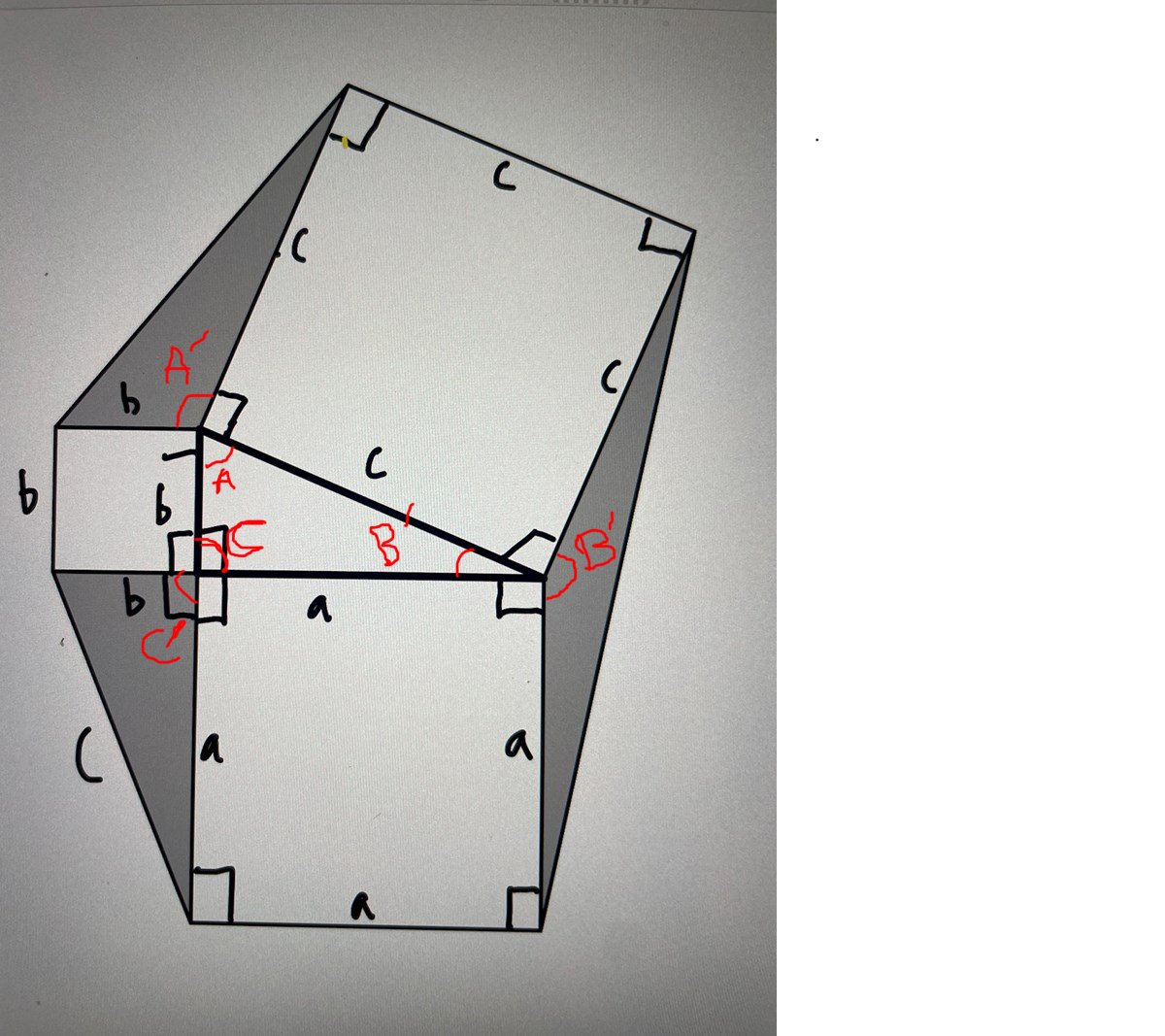
För vinkel-primvinkelparen gäller då
A + A' = 180 grader
B + B' = 180 grader
C + C' = 180 grader
Sedan kan du använda areasatsen i kombination med att
sin(A') = sin(180 - A) = sin(A)
dvs att sin av primvinklarna är samma som sin av triangelns vinklar.
Det visar sig att de mörka trianglarna har samma area som den rätvinkliga triangeln och detta gäller även om mitttriangeln är rätvinklig eller ej.
Om du vill bevisa påståendet utan trigonometri så får man använda pythagoras sats på finurliga vis. Ett vis är att helt enkelt rita "storkvadraten" från standardbeviset för pythagoras sats och notera konruenser.

Övre vänstra vinkeln i den inre triangeln kan vi kalla A. Då är sin(A) = a/c. Bredvid den vinkeln finns två räta vinklar, så den återstående vinkeln där är också A. Arean av den gråa ytan får du med areasatsen.
Lite overkill.
Utan trigonometri:
Den högra triangeln har en sida som är a och höjden (med den sidan som bas) är b eftersom den triangel som bildas av de röda linjerna höger tillsammans med en sida c ovan är kongruent med den nedre vänstra.
Den översta har en sida b och att höjden är a framgår av en kongruent triangel med c och röda linjer upp til vänster.



