Area under graf
Uppgift 63. Det känns som att jag har gjort helt rätt. Jag har även kontroll räknat. Men jag fattar inte varför jag får ett fel svar. 
Som du beräknade så blir tangent funktionen g(x) = 9ln(3)x+9-ln(3)18 på punkten (2,9) av funktionen f(x) = 3x. Då man graphar detta så bildar det en triangel på fjärde kvadranten som bilden visar.
Då man vet detta så är det bara att hitta hörnen av triangeln som är (0,0), (x-1/ln(3)) och (0,9-ln(3)*18), detta får du genom att lösa g(x) = 0 och räkna g(0). När du har detta så använder du area formeln for triangeln.
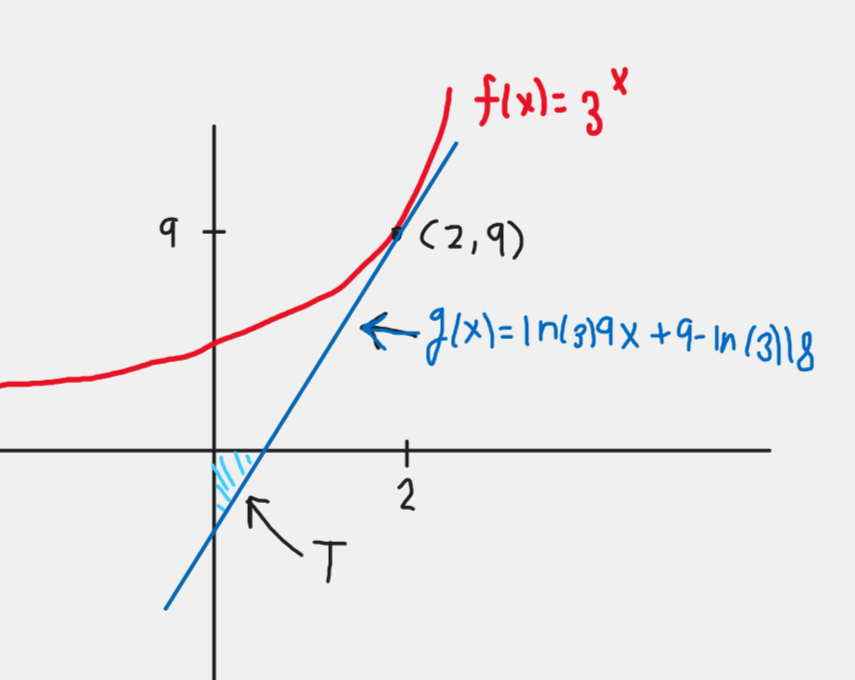
Tack! Som jag har gjort här borde det inte vara något fel men enligt facit är min y-värde vänd.
Värdet y(0)=9−18ln(3) är i sig korrekt.
Vid geometriska volymberäkningar kräver man dock alltid ett positivt resultat. I andra sammanhang kan det däremot vara praktiskt att låta volymen vara tecknad (dvs. ha både positiva och negativa värden).
Eftersom 9−18ln(3)<0 kan vi byta teckenled och få 18ln(3)−9>0.
