2
svar
245
visningar
Arean
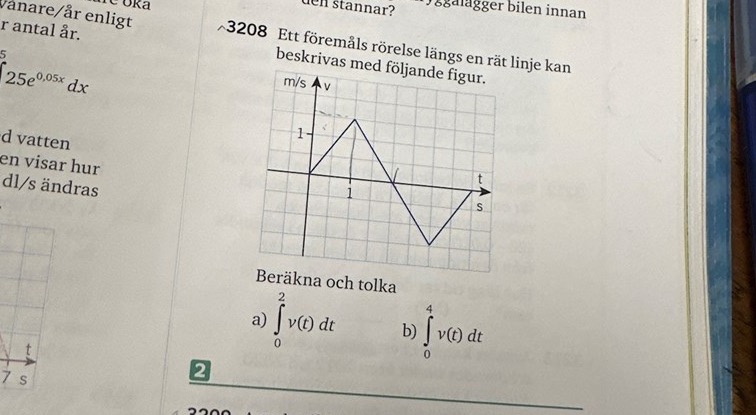 Går det att göra såhär? A) blir det problem med b) då?
Går det att göra såhär? A) blir det problem med b) då?

Så kan du nog tänka.
Dock är iden med dessa uppgifter att du ska använda den geometriska uppfattningen av integralen: arean under kurvan. För a) ser vi att integralen motsvarar en triangel med bas och höjd .
Då kan vi bara beräkna integralen som arean på en triangel:
För b) måste du komma ihåg att integralen beräknar tecknad area. Arean under x-axeln får ett negativt värde.
 Såhär?
Såhär?

