Arean A2 över y=e^x är ekvivalent med A1 under y=e^x från 0 till a. Vad är a?
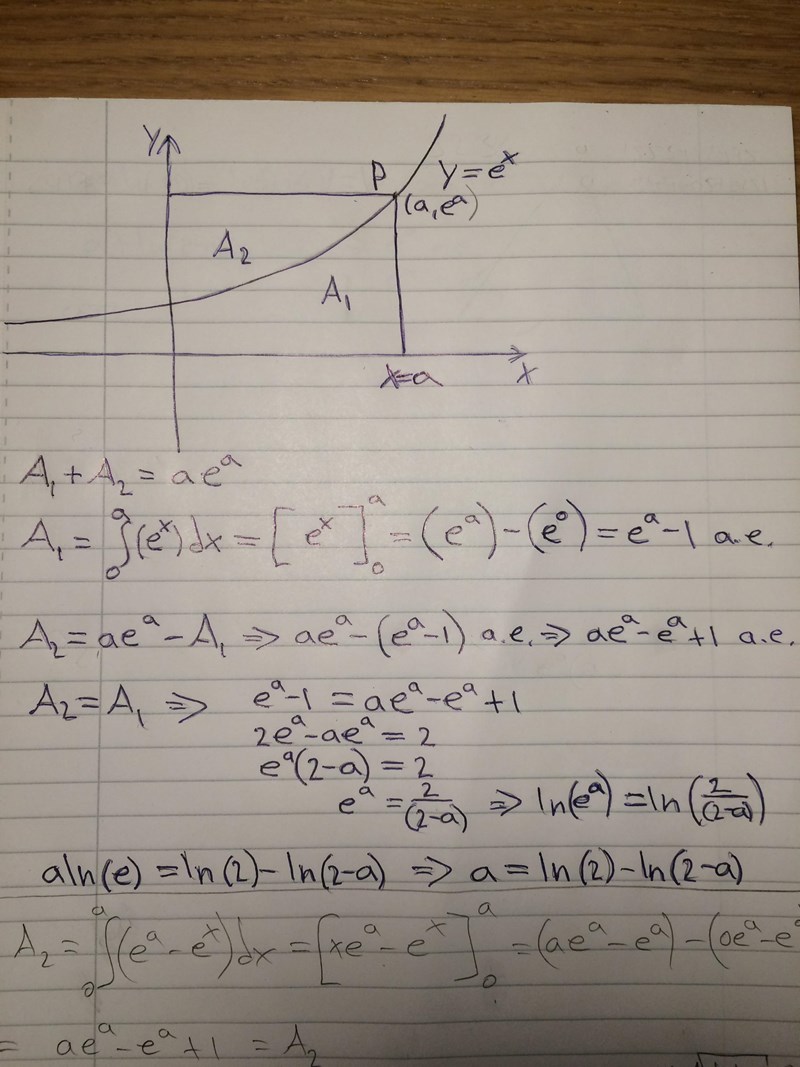 Som rubriken säger är arean A2 över y=e^x lika med A1 under y=e^x från x=0 till x=a. Vad ska a vara för att dessa två areor ska vara lika? Punkten P på grafen delar alltså arean lika i två delar A1 och A2. Arean för hela geometriska figuren är basen a gånger höjden e^a. P(a,e^a). Vad ska a vara för att areorna ska vara lika med varandra? Jag har påbörjat lösningen, men kommer inte längre än på bilden.
Som rubriken säger är arean A2 över y=e^x lika med A1 under y=e^x från x=0 till x=a. Vad ska a vara för att dessa två areor ska vara lika? Punkten P på grafen delar alltså arean lika i två delar A1 och A2. Arean för hela geometriska figuren är basen a gånger höjden e^a. P(a,e^a). Vad ska a vara för att areorna ska vara lika med varandra? Jag har påbörjat lösningen, men kommer inte längre än på bilden.
Tror inte du kan lösa den exakt för hand, jag skulle bara använt grafräknare
Är du säker? Hur använder man grafritaren för att bestämma värdet på x=a?
Jag håller med om att man inte kan lösa den exakt med standardfunktioner. Ett numeriskt sätt är att iterera sig fram. Man "löser ut" a som en funktion av a:
Sedan tar man något bra startvärde på a, t.ex. 1, och kör några varv tills man är nöjd.
f(1) = 1.264
f(1.264) = 1.435
f(1.435) = 1.524
f(1.524) = 1.564
osv.
Partykoalan skrev:Är du säker? Hur använder man grafritaren för att bestämma värdet på x=a?
Ja den ska du lösa numeriskt eller grafiskt.
Vilken metod du ska använda framgår nog av sammanhanget. Vad heter avsnittet i boken där uppgiften finns?
Och hur du ska lösa ekvationen med grafräknare beror på vilken räknare du har.
Nedan är en numerisk metod som ofta används i dylika fall:

Grafisk metod är nog mer rättfram att förstå om du inte har lärt dig om numeriska metoder att lösa ekvationer. (Fast en numerisk metod är mer elegant, så fördjupa dig gärna i det...)
Den grafiska metoden är helt enkelt så att du löser ekvationen genom att plotta kurvan och zooma in i grafen för att se för vilket x-värde som y blir 0 (kurvans skärning med x-axeln). Klart!
(On a side note, jag satt också halva natten och klurade på att försöka hitta ett analytiskt sätt att lösa ekvationen ;-))
Hej allihopa och tack för era svar!
Vi har inte arbetat med numeriska metoder, så en grafisk lösning för detta fall är nog lite simplare och kanske ger ett säkrare värde för x=a. I detta fall är det tillåtet att använda räknare, så jag antar att räknare är ett verktyg som ska användas för att kunna lösa uppgiften grafiskt.
Det har dock aldrig fallit mig in att jag var så nära lösningen genom att knappa in variablerna och skapa en kurva som ska skära x=0, dvs x-axeln och utläsa värdet för skärningspunkten.
Hur som helst fick jag att arean är 3,92 a.e. för både A1 och A2 om x=a=1,59, vilket verkar rimligt. Vad tycker ni? Haha skönt att veta att man inte var ensam om att försöka hitta en lösningsmetod för ekvationen.
Din räknare har antagligen en funktion som heter "Intersect" eller liknande.
Då använder räknaren internt någon numerisk metod för att ta fram ett närmevärde på x.
Partykoalan skrev:
Hur som helst fick jag att arean är 3,92 a.e. för både A1 och A2 om x=a=1,59, vilket verkar rimligt. Vad tycker ni? Haha skönt att veta att man inte var ensam om att försöka hitta en lösningsmetod för ekvationen.
Min talserie kanske närmar sig 1,59.
Ett litet Python-skript nedan för fixpunktsiterationen:
import math
a_prev=0
a=1
print('a = ', a)
while abs(a-a_prev)>1e-6:
a_prev=a
a=2-2/math.exp(a)
print('a = ', a)
Ger följande resultat:
a = 1
a = 1.2642411176571153
a = 1.4350928722989194
a = 1.5238134985594098
a = 1.5642411643895795
a = 1.581506526363297
a = 1.588669950170612
a = 1.5916059531703466
a = 1.5928032408367592
a = 1.5932904807529327
a = 1.593488597595861
a = 1.5935691263742027
a = 1.593601854438143
a = 1.5936151548449866
a = 1.5936205598928175
a = 1.5936227563871928
a = 1.5936236489915423
Newton-Raphson:
import math
a_prev=0
a=1
print('a = ', a)
while abs(a-a_prev)>1e-6:
a_prev=a
a=a-(2-a-2*math.exp(-a))/(-1+2*math.exp(-a))
print('a = ', a)
Detta ger följande svar:
a = 1
a = 2.0
a = 1.6288774948182745
a = 1.5940301554289886
a = 1.5936243164007198
a = 1.5936242600400412
Slutligen sekantmetoden: https://sv.wikipedia.org/wiki/Sekantmetoden
import math
a_prev2=1
a_prev1=2
print('a = ', a_prev1)
while True:
a=a_prev1-(a_prev1-a_prev2)/((2-a_prev1-2*math.exp(-a_prev1))-(2-a_prev2-2*math.exp(-a_prev2)))*(2-a_prev1-2*math.exp(-a_prev1))
print('a = ', a)
if abs(a-a_prev1)<1e-6:
print('Klart!')
break
else:
a_prev2=a_prev1
a_prev1=a
Den ger följande resultat:
a = 2
a = 1.493990177250883
a = 1.5820890819589652
a = 1.5940493299143499
a = 1.5936225690467833
a = 1.5936242597940804
a = 1.5936242600400403
Klart!
Lämnar som uppgift, för den intresserade, att lösa denna uppgift numeriskt, medelst Python eller annat programmeringsspråk med någon av följande metoder:
Halley's metod: https://en.wikipedia.org/wiki/Halley%27s_method
Steffensen's method: https://en.wikipedia.org/wiki/Steffensen%27s_method
Inverse quadratic interpolation: https://en.wikipedia.org/wiki/Inverse_quadratic_interpolation
Din räknare har antagligen en funktion som heter "Intersect" eller liknande.
Då använder räknaren internt någon numerisk metod för att ta fram ett närmevärde på x.
Precis!
Jag knappade in 2e^x-xe^x-2 och sedan tryckte jag ZERO, vilket söker nollvärden. Då fick jag att x= 1,5936243 när y=0
Jag har en Texas TI 84 Plus grafritare






