Arean av en ellips

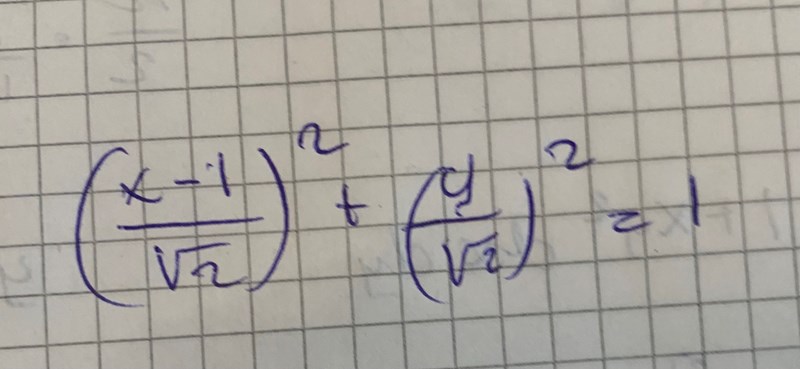
sin 2x skrev:

Hej! 

skärningen mellan ytan z=x^2 + z^2 och planet z=1+ 2x blir en ellips och jag undrar hur man räknar arean av det 

jag fick denna ekvation med hjälp av kvadrat komplettering  

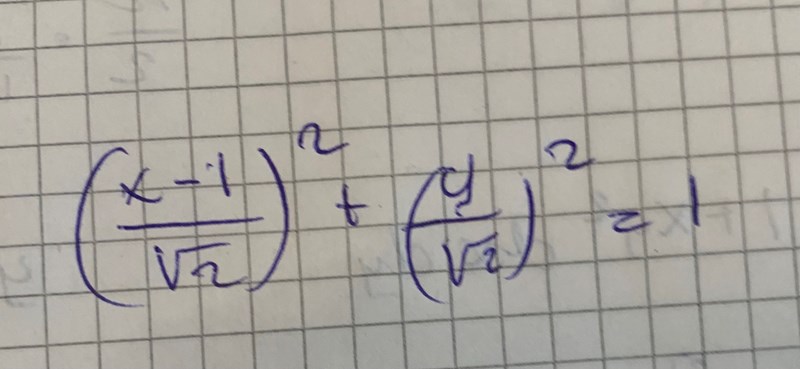
Det där ser ut som en cirkel, inte en ellips. 

i facit står det att de ska vara en ellips, hur ska man göra då för att det bli en ellips? 

skärningen mellan ytan z=x^2 + z^2 och planet z=1+ 2x blir en ellips

Skall det vara z = x²+y² eller skall det vara som det står?

sin 2x skrev:

i facit står det att de ska vara en ellips, hur ska man göra då för att det bli en ellips? 

Din cirkel är ellipsens projektion på xy-planet. Om en ellips i planet z = 1 + 2x blir en cirkel med radie sqrt(2) då den projiceras på xy-planet vilken area har ellipsen då?

Vad menas med att min cirkel är ellipsens projektion på xy-planet?

Se figur.

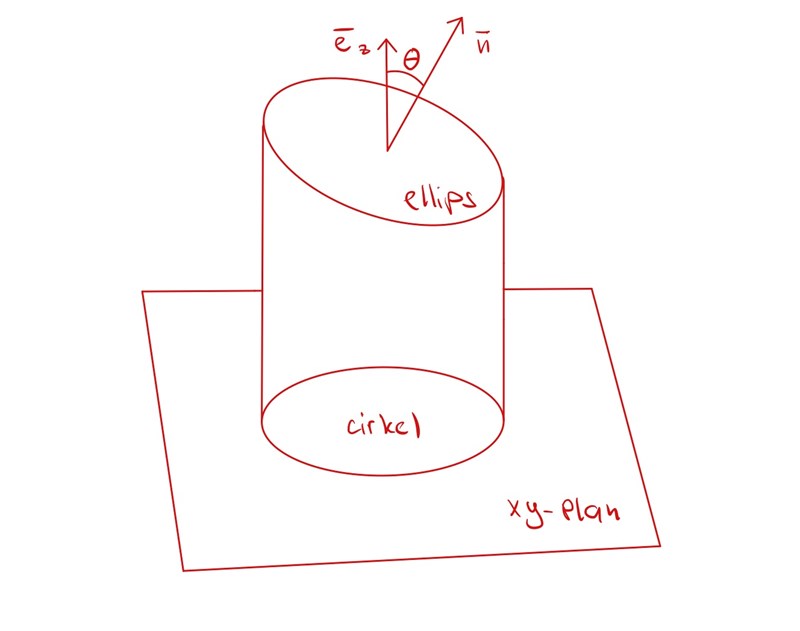
jag förstår nu, men hur räknar man då arean och va hjälper dehär oss?

Area _cirkel = cos($\theta$)Area_ellips.

Va beror vinkeln på då? 

Vinkeln är vinkeln mellan normalen till ellipsytan och vektorn (0, 0, 1).

cos($\theta$) = (0, 0, 1)•$\frac{\overrightarrow{n}}{\left|\overrightarrow{n}\right|}$.

Du kan också parametrisera ellipsytan, tex kan vi låta x och y vara oberoende variabler.

$\overrightarrow{r}$ = (x, y, 1 + 2x).

$d\overrightarrow{S}$ = $\frac{\partial \overrightarrow{r}}{\partial x}\times \frac{\partial \overrightarrow{r}}{\partial y}$$dxdy$ = (-2, 0, 1)$dxdy$.

rot$\overrightarrow{F}$ = (-1, 0, 1).

$\underset{ellips}{\iint }rot\overrightarrow{F}\bullet d\overrightarrow{S}=\underset{C}{\iint }(-1, 0, 1)\bullet (-2, 0, 1)dxdy=3\underset{C}{\iint }dxdy=3·2\mathrm{\pi }=6\mathrm{\pi }.$

Där C är cirkelskivan i xy-planet.