Arean av två trig funktioner

Jag antar att det är det här området vi är intresserade av

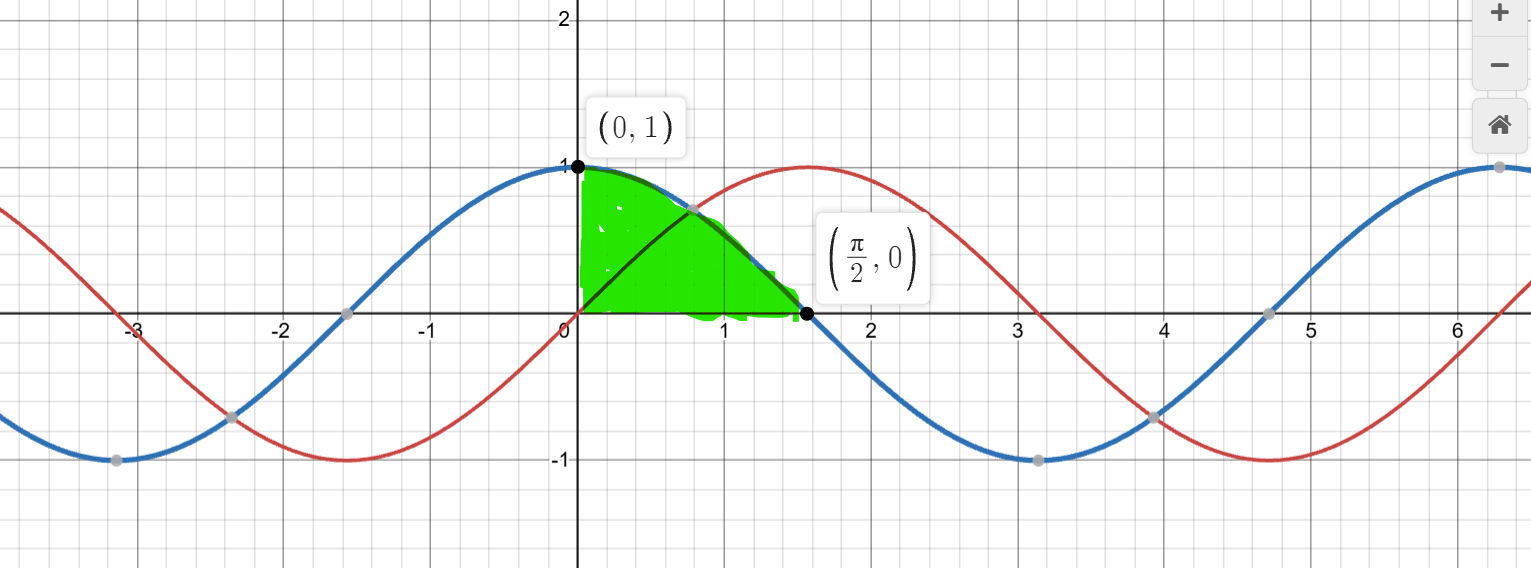
Utnyttja symmetri.

Hur menar du då ?

borde jag inte börja med att ta reda på nollställena ?

Arup skrev:

Hur menar du då ?

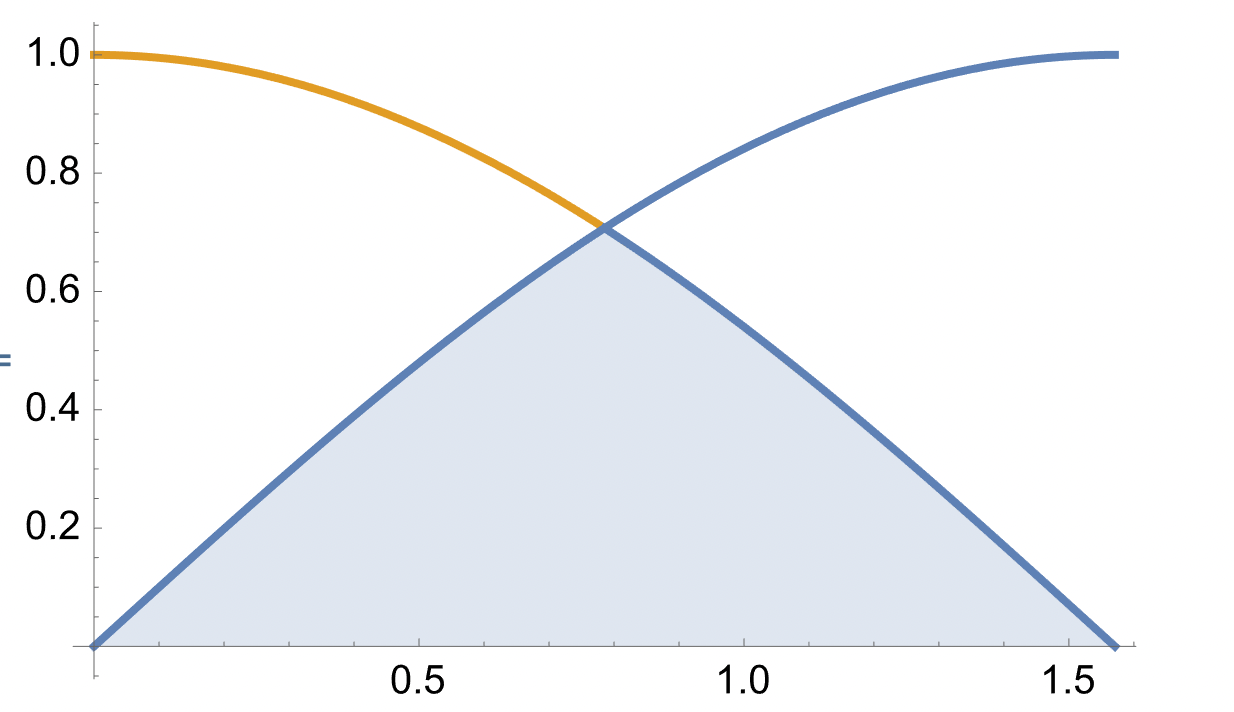
Det är det rödfärgade området som avses:

Arup skrev:

borde jag inte börja med att ta reda på nollställena ?

Ja, det är en bra idé.

Sedan bör du även bestämma x-koordinaten för skärningspunkten mellan de två graferna.

Kan man dela det med två eftersom det är en symmetri som Trinity skrev i #3 ?

Är sdt så här ?

Arup skrev:

Kan man dela det med två eftersom det är en symmetri som Trinity skrev i #3 ?

Ja, det går bra.

Arup skrev:

Är sdt så här ?

Inte riktigt.

Det stämmer att skärningspunkten är x = pi/4, men din integral stämmer inte. Ser du varför?

Om inte, förklara varför du valde just den integranden och visa gärna med bild vilket område du areaberäknar med hjälp av integralen..

borde det vara 

${\int }_0^{\frac{\mathrm{\pi }}{4}}\cos \left(x\right)-\sin \left(x\right)dx$?

Arup skrev:

borde det vara 

${\int }_0^{\frac{\mathrm{\pi }}{4}}\cos \left(x\right)-\sin \left(x\right)dx$?

Det är fel område.

Arup skrev:

borde det vara 

${\int }_0^{\frac{\mathrm{\pi }}{4}}\cos \left(x\right)-\sin \left(x\right)dx$?

Varför då?

Tänk på att arean av ett område kan beräknas som integralen av ("övre funktion" minus "undre funktion")

Visa i denna bild vilket område du avser med din integral: