Areasatsen bevis
Hallå, behöver lite hjälp med att förstå areasatsen..
Alla bevis jag läser använder sig av rätvinkliga trianglar i en godtycklig triangel för att visa areasambandet..
Typ i figuren nedan kan man skriva att h = bSINA
Och h = aSINB
Då är det superlogiskt att arean blir cbSINA/2 och caSINB/2. Men tycker tycker inte abSINC/2 är speciellt logiskt. Då ska alltså b×SINC = h, men det stämmer inte.. så, ja, varför är det sant undrar jag.

Vi kallar punkten med den räta vinkeln för D.
Först kan vi börja med att hitta en formel för arean med längderna i bilden. Basen gånger höjden/2 ger att
Area=hc2
För att motivera anledningen till att hitta areasatsen kan vi säga att vi vill byta ut h eftersom höjden kan ofta vara lite strulig att få fram i en triangel. Därför är det ofta enklare att ha en areaformer som uttryckt i sidlängderna.
Om vi då kollar på den rätvinkliga triangeln ACD: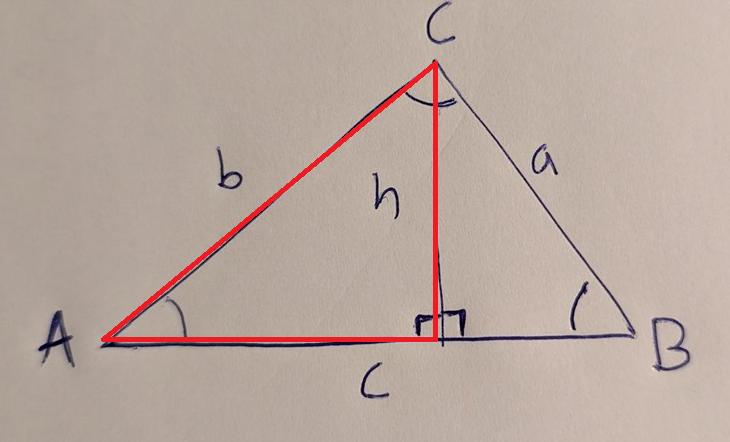
får vi att sinA=hb
Alltså är h=bsinA. Om vi byter ut h i formeln för area från förr får vi
Area=bcsinA2
Precis på samma sätt kan vi kolla på den andra rätvinkliga triangeln i bilden. Alltså BCD:
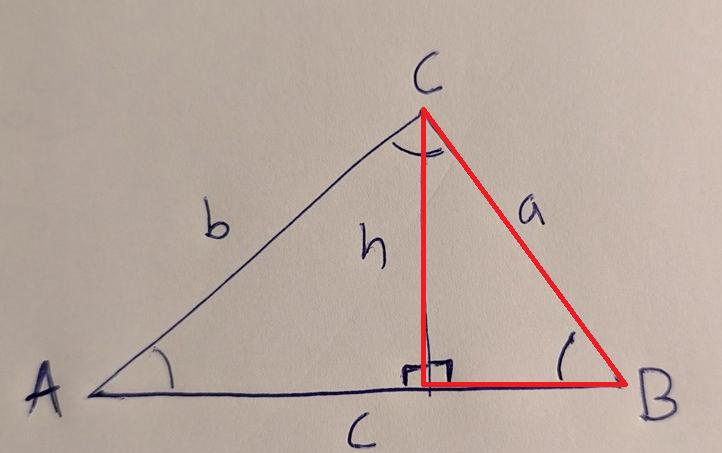
Då får vi att sinB=ha⇔ h=asinB vilket igen, ger att Area=acsinB2
Ber om ursäkt! Missade att du frågade om sin C
Hej Alex,
Ja, absolut. Men det sista sambandet, abSIN(C)/2, vart kommer det ifrån?
Det där beviset lyfter bara två samband, hittar inte någonstans där man bevisar det sista..Eller är det sista så självklart på något sätt att det inte behöver förklaras?
Ah, såg din kommentar nu. Skulle ha uttryckt det tidigare i inlägget..
Dkcre skrev:Hej Alex,
Ja, absolut. Men det sista sambandet, abSIN(C)/2, vart kommer det ifrån?
Det där beviset lyfter bara två samband, hittar inte någonstans där man bevisar det sista..Eller är det sista så självklart på något sätt att det inte behöver förklaras?
Istället för att dra höjden från vinkeln C, kan vi lika gärna dra en linje från A eller B och på så sätt kan vi visa fallet för C. Vi kan använda samma triangel för det, kanske bara blir lite knöligt med hur det ser ut när det är utritat.
Det tredje fallet följer också från sinussatsen, sinAa=sinBb=sinCc.
Om vi utgår från (jag kommer använda T för att representera arean av triangeln)
T=bcsinA2⇔ . Om vi delar med på båda sidor får vi
Om vi löser ut får vi att
Dock tror jag inte att man ska använda sinussatsen för att bevisa areasatsen, de säger mycket liknande saker. Men det är intressant att se sambanden!
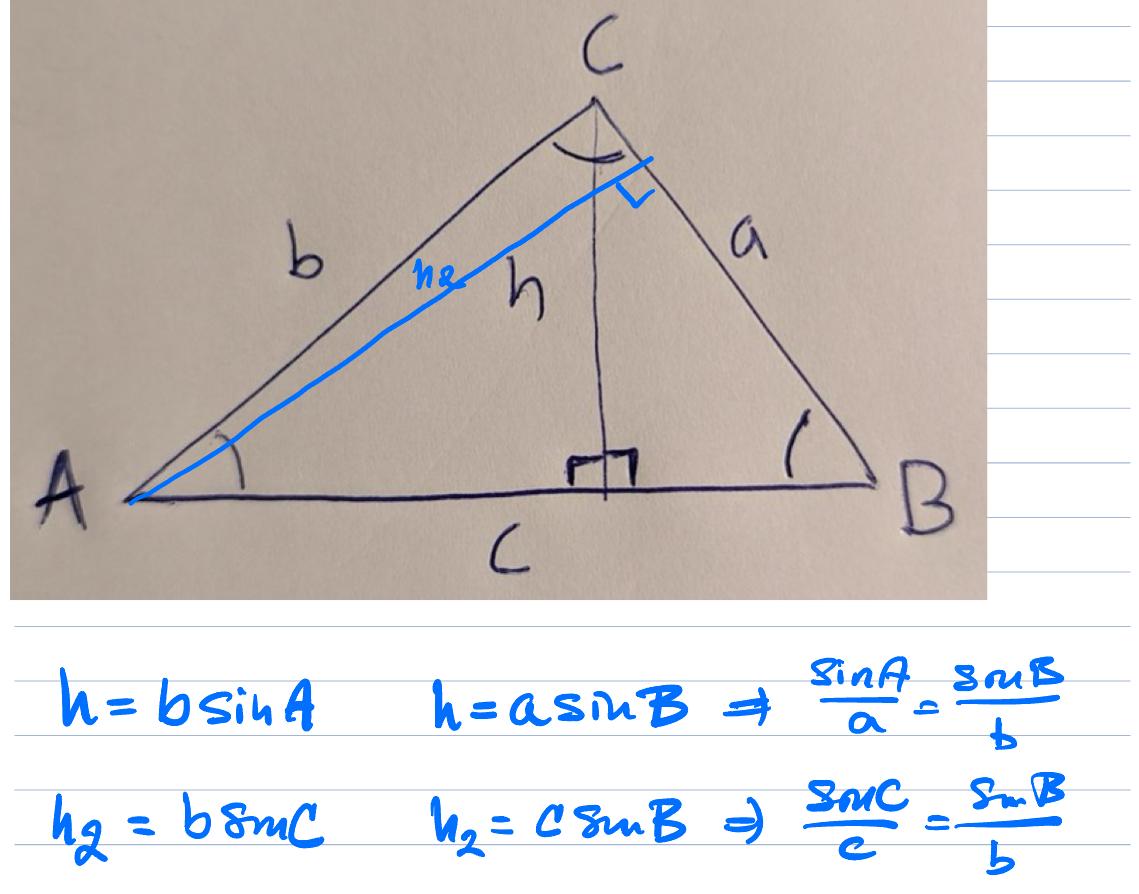
Drag en ny höjd
AlexMu skrev:Dkcre skrev:Hej Alex,
Ja, absolut. Men det sista sambandet, abSIN(C)/2, vart kommer det ifrån?
Det där beviset lyfter bara två samband, hittar inte någonstans där man bevisar det sista..Eller är det sista så självklart på något sätt att det inte behöver förklaras?
Istället för att dra höjden från vinkeln C, kan vi lika gärna dra en linje från A eller B och på så sätt kan vi visa fallet för C. Vi kan använda samma triangel för det, kanske bara blir lite knöligt med hur det ser ut när det är utritat.
Det tredje fallet följer också från sinussatsen, .
Om vi utgår från (jag kommer använda för att representera arean av triangeln). Om vi delar med på båda sidor får vi
Om vi löser ut får vi attDock tror jag inte att man ska använda sinussatsen för att bevisa areasatsen, de säger mycket liknande saker. Men det är intressant att se sambanden!
Fattar, tack 👍
Trinity2 skrev:Drag en ny höjd
Tack :)



