Åskådliggör i det komplexa talplanet punkter för z
 Behöver hjälp med 4215 b, vet helt enkel inte hur man ska göra. Har ritat denna bild:
Behöver hjälp med 4215 b, vet helt enkel inte hur man ska göra. Har ritat denna bild:
Hur gjorde du då med a?
Lösningspunkter i b har samma avstånd till i och till 2.
Markera en godtycklig punkt z i det komplexa planet.
Markera punkterna A = z – i och B = z – 2.
Var ska z ligga för att A och B ska ligga lika långt från origo?
EDIT: Peter Kuipers lösningsförslag var smartare. Glöm detta.
Marilyn skrev:Markera en godtycklig punkt z i det komplexa planet.
Markera punkterna A = z – i och B = z – 2.
Var ska z ligga för att A och B ska ligga lika långt från origo?
Avståndet från origo spelar ingen roll i uppgift b.
Det är nog lättast att börja med en punkt som ligger lika långt från i som från 2.
Pieter Kuiper skrev:Marilyn skrev:Markera en godtycklig punkt z i det komplexa planet.
Markera punkterna A = z – i och B = z – 2.
Var ska z ligga för att A och B ska ligga lika långt från origo?
Avståndet från origo spelar ingen roll i uppgift b.
Det är nog lättast att börja med en punkt som ligger lika långt från i som från 2.
Först, din lösning var smartare. Jag har inte tänkt så förut.
Men om |z–i| = |z–2| så är väl punkterna z–i och z–2 lika långt från origo?
Marilyn skrev:Pieter Kuiper skrev:Marilyn skrev:Markera en godtycklig punkt z i det komplexa planet.
Markera punkterna A = z – i och B = z – 2.
Var ska z ligga för att A och B ska ligga lika långt från origo?
Avståndet från origo spelar ingen roll i uppgift b.
Det är nog lättast att börja med en punkt som ligger lika långt från i som från 2.
Först, din lösning var smartare. Jag har inte tänkt så förut.
Men om |z–i| = |z–2| så är väl punkterna z–i och z–2 lika långt från origo?
Nej, |z–i| = |z–2| beskriver de z som ligger på lika avstånd från i resp. 2.
Det triviala z som uppfyller detta är det z som ligger mitt emellan i och 2.
d.v.s. mittpunken på

Sedan är resten lätt (när man väl har gjort denna typ av uppgift en gång...). Från denna punkt, drag en normal till linjen mellan i och 2 (en s.k. mittpunktsnormal). Alla punkter på normalen uppfyller |z–i| = |z–2| .
Pieter Kuiper skrev:Det är nog lättast att börja med en punkt som ligger lika långt från i som från 2.
Eller man ritar två cirklar med lika stora radier kring i och kring 2. Då får man två lösningar på skärningspunkterna. Även det leder snabbt till mittpunktsnormalen.
Peter Kuiperskriver:
"Nej, |z–i| = |z–2| beskriver de z som ligger på lika avstånd från i resp. 2."

Trinity2 skrev:Marilyn skrev:Pieter Kuiper skrev:Marilyn skrev:Markera en godtycklig punkt z i det komplexa planet.
Markera punkterna A = z – i och B = z – 2.
Var ska z ligga för att A och B ska ligga lika långt från origo?
Avståndet från origo spelar ingen roll i uppgift b.
Det är nog lättast att börja med en punkt som ligger lika långt från i som från 2.
Först, din lösning var smartare. Jag har inte tänkt så förut.
Men om |z–i| = |z–2| så är väl punkterna z–i och z–2 lika långt från origo?
Nej, |z–i| = |z–2| beskriver de z som ligger på lika avstånd från i resp. 2.
Det triviala z som uppfyller detta är det z som ligger mitt emellan i och 2.
d.v.s. mittpunken på
Sedan är resten lätt (när man väl har gjort denna typ av uppgift en gång...). Från denna punkt, drag en normal till linjen mellan i och 2 (en s.k. mittpunktsnormal). Alla punkter på normalen uppfyller |z–i| = |z–2| .
Tack! i facit står det att man ska skriva en formel får linjen som går mellan i och 2, vet dock inte hur
Koizenu skrev:Trinity2 skrev:Marilyn skrev:Pieter Kuiper skrev:Marilyn skrev:Markera en godtycklig punkt z i det komplexa planet.
Markera punkterna A = z – i och B = z – 2.
Var ska z ligga för att A och B ska ligga lika långt från origo?
Avståndet från origo spelar ingen roll i uppgift b.
Det är nog lättast att börja med en punkt som ligger lika långt från i som från 2.
Först, din lösning var smartare. Jag har inte tänkt så förut.
Men om |z–i| = |z–2| så är väl punkterna z–i och z–2 lika långt från origo?
Nej, |z–i| = |z–2| beskriver de z som ligger på lika avstånd från i resp. 2.
Det triviala z som uppfyller detta är det z som ligger mitt emellan i och 2.
d.v.s. mittpunken på
Sedan är resten lätt (när man väl har gjort denna typ av uppgift en gång...). Från denna punkt, drag en normal till linjen mellan i och 2 (en s.k. mittpunktsnormal). Alla punkter på normalen uppfyller |z–i| = |z–2| .
Tack! i facit står det att man ska skriva en formel får linjen som går mellan i och 2, vet dock inte hur
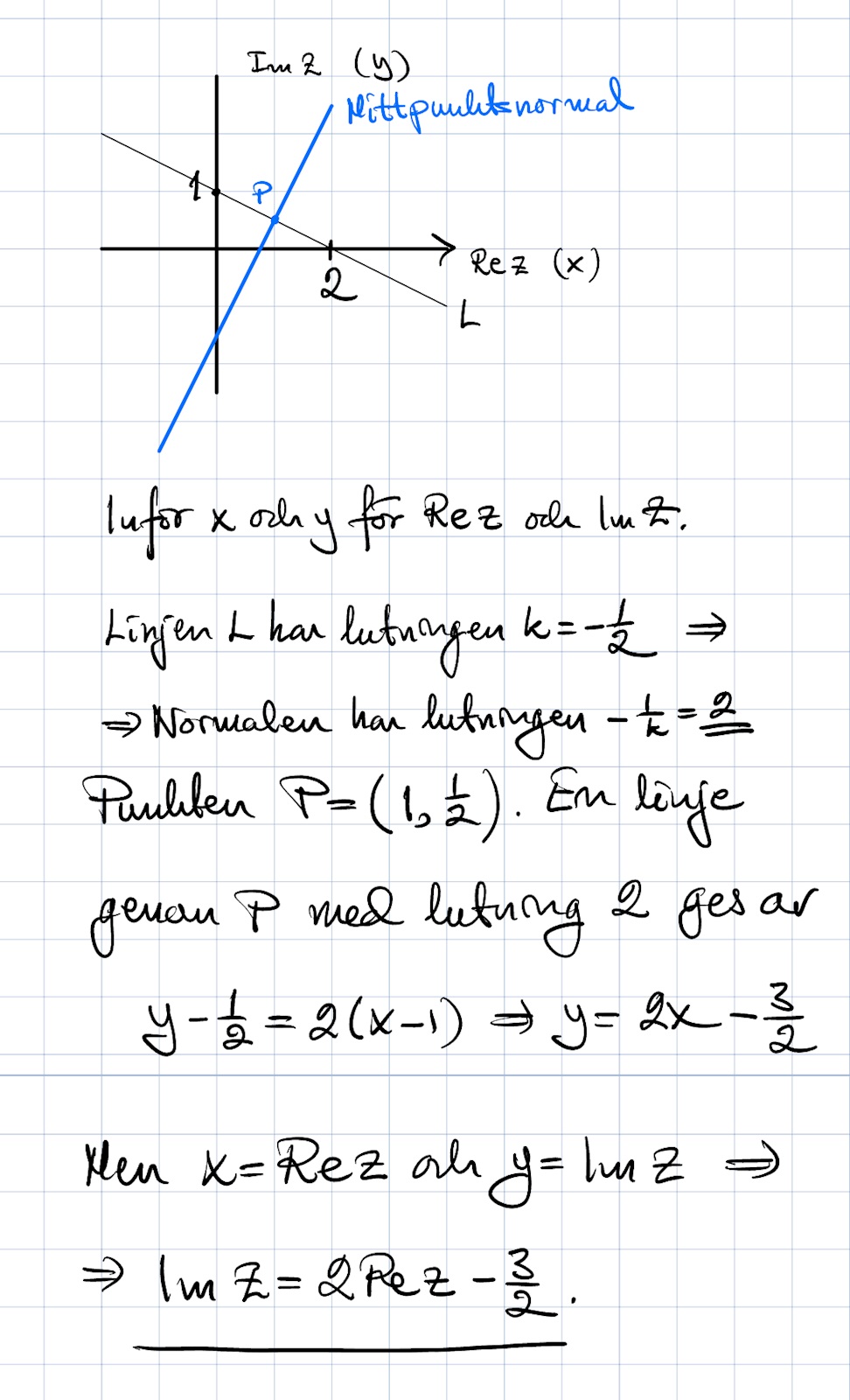
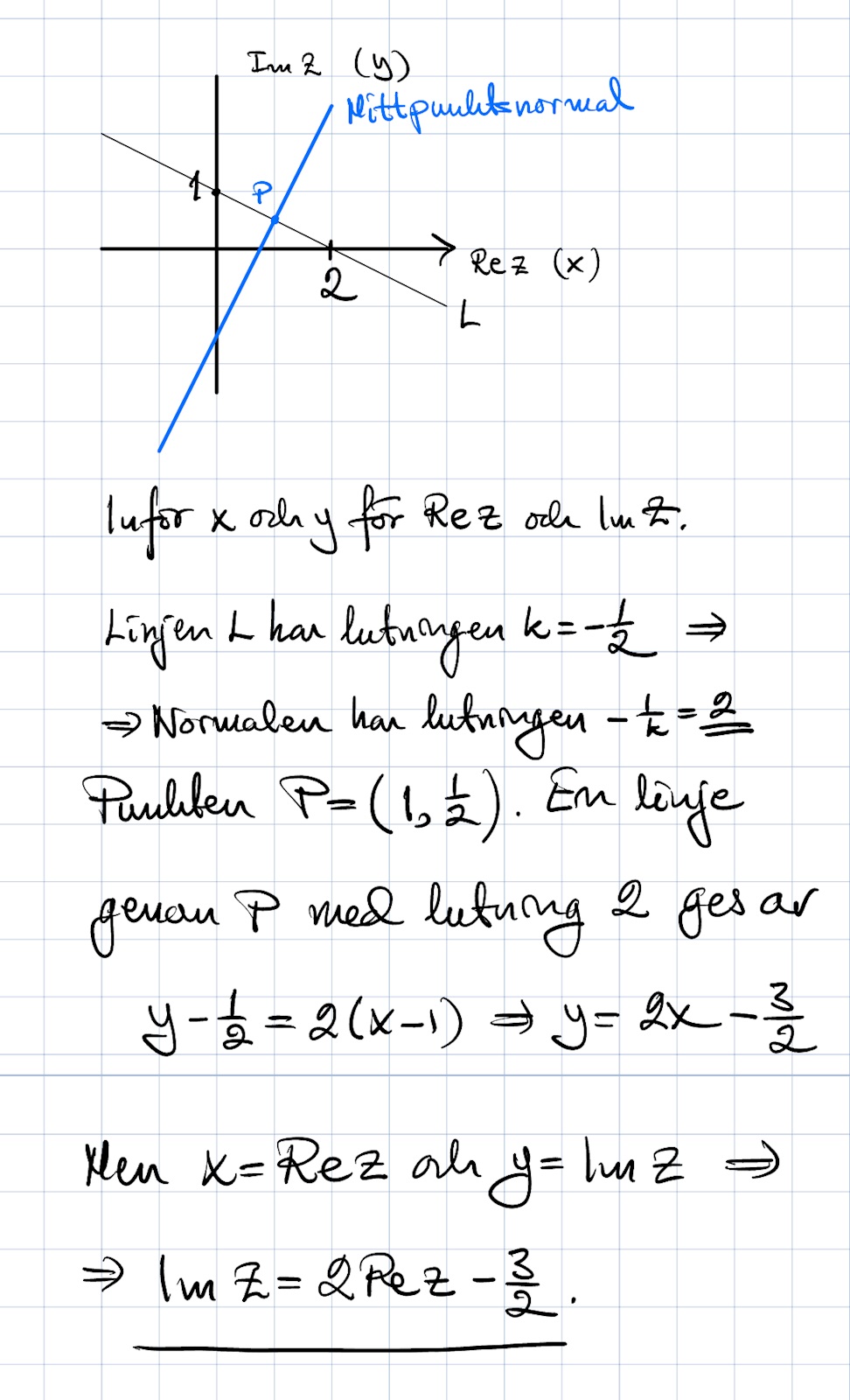
Koizenu skrev:i facit står det att man ska skriva en formel får linjen som går mellan i och 2, vet dock inte hur
Konstigt. I uppgiften står att man ska "åskådliggöra" och då borde det räcka med att rita.
Någon ritning kanske inte syns i facit, men utan den skulle jag inte tro att man fick poäng. Så, hade du själv ritat något mer? Gjort något med alla tips här hur man kunde börja?
Pieter Kuiper skrev:Koizenu skrev:i facit står det att man ska skriva en formel får linjen som går mellan i och 2, vet dock inte hur
Konstigt. I uppgiften står att man ska "åskådliggöra" och då borde det räcka med att rita.
Någon ritning kanske inte syns i facit, man utan den skulle jag inte tro att man fick poäng. Så, hade du själv ritat något mer? Gjort något med alla tips här hur man kunde börja?
Håller med. En bild borde räcka.
Trinity2 skrev:Koizenu skrev:Trinity2 skrev:Marilyn skrev:Pieter Kuiper skrev:Marilyn skrev:Markera en godtycklig punkt z i det komplexa planet.
Markera punkterna A = z – i och B = z – 2.
Var ska z ligga för att A och B ska ligga lika långt från origo?
Avståndet från origo spelar ingen roll i uppgift b.
Det är nog lättast att börja med en punkt som ligger lika långt från i som från 2.
Först, din lösning var smartare. Jag har inte tänkt så förut.
Men om |z–i| = |z–2| så är väl punkterna z–i och z–2 lika långt från origo?
Nej, |z–i| = |z–2| beskriver de z som ligger på lika avstånd från i resp. 2.
Det triviala z som uppfyller detta är det z som ligger mitt emellan i och 2.
d.v.s. mittpunken på
Sedan är resten lätt (när man väl har gjort denna typ av uppgift en gång...). Från denna punkt, drag en normal till linjen mellan i och 2 (en s.k. mittpunktsnormal). Alla punkter på normalen uppfyller |z–i| = |z–2| .
Tack! i facit står det att man ska skriva en formel får linjen som går mellan i och 2, vet dock inte hur
Tack!!
Det kan vara intressant att jämföra med min metod (ja, jag vet att den är krångligare, men en omväg kan erbjuda andra vyer).
Låt z = a+bi. Jag skriver (a, b).
Då är z–2 = (a–2, b) och z–i = (a, b–1)
Det ger (a–2)2 + b2 = a2 + (b–1)2
Kvadraterna försvinner, så vi får lätt b = 2a–3/2 dvs
z = a + (2a–3/2)i ; a reellt.
Trinity2 skrev:Koizenu skrev:Trinity2 skrev:Marilyn skrev:Pieter Kuiper skrev:Marilyn skrev:Markera en godtycklig punkt z i det komplexa planet.
Markera punkterna A = z – i och B = z – 2.
Var ska z ligga för att A och B ska ligga lika långt från origo?
Avståndet från origo spelar ingen roll i uppgift b.
Det är nog lättast att börja med en punkt som ligger lika långt från i som från 2.
Först, din lösning var smartare. Jag har inte tänkt så förut.
Men om |z–i| = |z–2| så är väl punkterna z–i och z–2 lika långt från origo?
Nej, |z–i| = |z–2| beskriver de z som ligger på lika avstånd från i resp. 2.
Det triviala z som uppfyller detta är det z som ligger mitt emellan i och 2.
d.v.s. mittpunken på
Sedan är resten lätt (när man väl har gjort denna typ av uppgift en gång...). Från denna punkt, drag en normal till linjen mellan i och 2 (en s.k. mittpunktsnormal). Alla punkter på normalen uppfyller |z–i| = |z–2| .
Tack! i facit står det att man ska skriva en formel får linjen som går mellan i och 2, vet dock inte hur
hur fick du reda på punkten (1, 1/2)?