Astrofysik-dopplereffekten med ljus

$$\begin{gathered} \lambda = {\lambda }_0 +\Delta \lambda \\ \frac{\Delta \lambda }{{\lambda }_0} = 4,43 \Rightarrow \frac{\lambda }{{\lambda }_0} = \frac{{\lambda }_0 +\Delta \lambda }{{\lambda }_0} = 1 + \frac{\Delta \lambda }{{\lambda }_0} = 5,43 \end{gathered}$$

Jag förstod allt tills att ettan kom in. Varför blir ny våglängd/gammal våglängd=våglängdskillnad/gammal våglängd+1. Jag förstår alltså inte riktigt det sista steget. 

Hur skriver alla dessa olika tecken förresten? Hur får du fram dem?

Om ett värde ökar med 443%, så är det nya värdet 543% av det gamla.

När man skriver inlägg syns ett kvadratrotstecken bland symbolerna. Klicka på det, så kommer du till en formeleditor. Den kräver lite övning, men efter ett tag lär man sig hur den funkar.

Jag kunde ha tagit med mellansteget $\frac{{\lambda }_0 + \Delta \lambda }{{\lambda }_0} =\frac{{\lambda }_0}{{\lambda }_0} + \frac{\Delta \lambda }{{\lambda }_0} = 1 + \frac{\Delta \lambda }{{\lambda }_0}$ men jag trodde inte det skulle behövas.

Tack Bubo och smaragdalena! Nu förstår jag hur man löser det här problemet. 

I det första utkastet undrade jag varför den lösningen var fel. Nu när jag skriver in det på miniräknaren igen får jag rätt svar (2,36um). 

Tack!!!

I din andra uppgift kan du utnyttja att

$\frac{R(t_0)}{R(t_1)}-1=z$

Där R(t) är en sorts kosmologisk skalfaktor vid tiden t, av konvention sätter man alltid $t_0$ till tiden som råder just nu för dig som uppmäter något labbet och $t_1$ är tiden då ljusets sändes ut.  z eller rödförskjutningen är 4.43. Att z är så stor gör det lite kinky att "räkna" på  det sätt facit föreslår.

Tack Guggle!!!!

Men vad heter formeln?

Den heter inget särskilt utan är bara ett användbart (och välkänt) resultat av en geometrisk skalfaktor.

På gymnasienivå kan vi resonera ungefär såhär:

Ljus med våglängden $\lambda_1$ sänds ut från en galax (t.ex. med koordinaterna 3,3 i bilden) vid tidpunkten $t$. Vid  en senare tidpunkt $t_0$, när universum expanderat, har rutnätet som spänner upp universum blivit "större". Ljuset har färdats "sträckan" d, en sträcka som tänjts ut och blivit längre under tiden som ljuset har färdats på grund av expansionen (och når nu objektet i punkt 7,5).

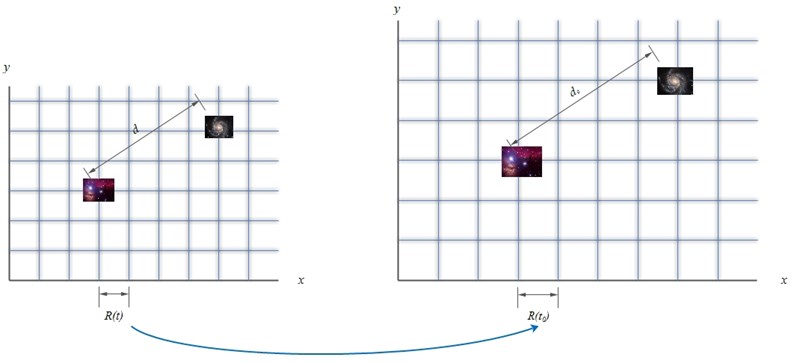
Notera att objekten fortfarande ligger kvar på samma koordinater, det är rutnätet i sig som blivit större.

Det betyder att universum har vuxit i storlek med en faktor $R(t_0 )/R(t)$ under tiden ljuset färdats till oss.

Då måste också dess våglängd ha vuxit med samma faktor $R(t 0 )/R(t)$ (vågtopparna dras isär av rutnätets expansion). När vi mäter ljuset ser vi att våglängden nu är $\lambda_0=\lambda_1 R(t_0)/R(t)$

Eftersom $\lambda_1$  bestäms av egenskaper hos den atom som sänder ut ljuset, och dessa egenskaper inte förändras med tiden vet vi hur mycket $\lambda_1$ har förändrats av rutnätets expansion. Det gör att vi kan bestämma skalfaktorns kvot.

För att erhålla formeln som använder z som du undrade över börjar vi med att subtrahera $\lambda_1$ från båda sidor

$\lambda_0-\lambda_1=\lambda_1 R(t_0)/R(t)-\lambda_1$

Sedan delar vi båda sidor med $\lambda_1$ för att jämföra "skillnaden" med det värde vi förväntar oss

$\frac{\lambda_0-\lambda_1}{\lambda_1}=R(t_0)/R(t)-1$

Slutligen inför vi rödförskjutningen z enligt ovan och erhåller

$z=R(t_0)/R(t)-1$