Asymptoter hyperbel

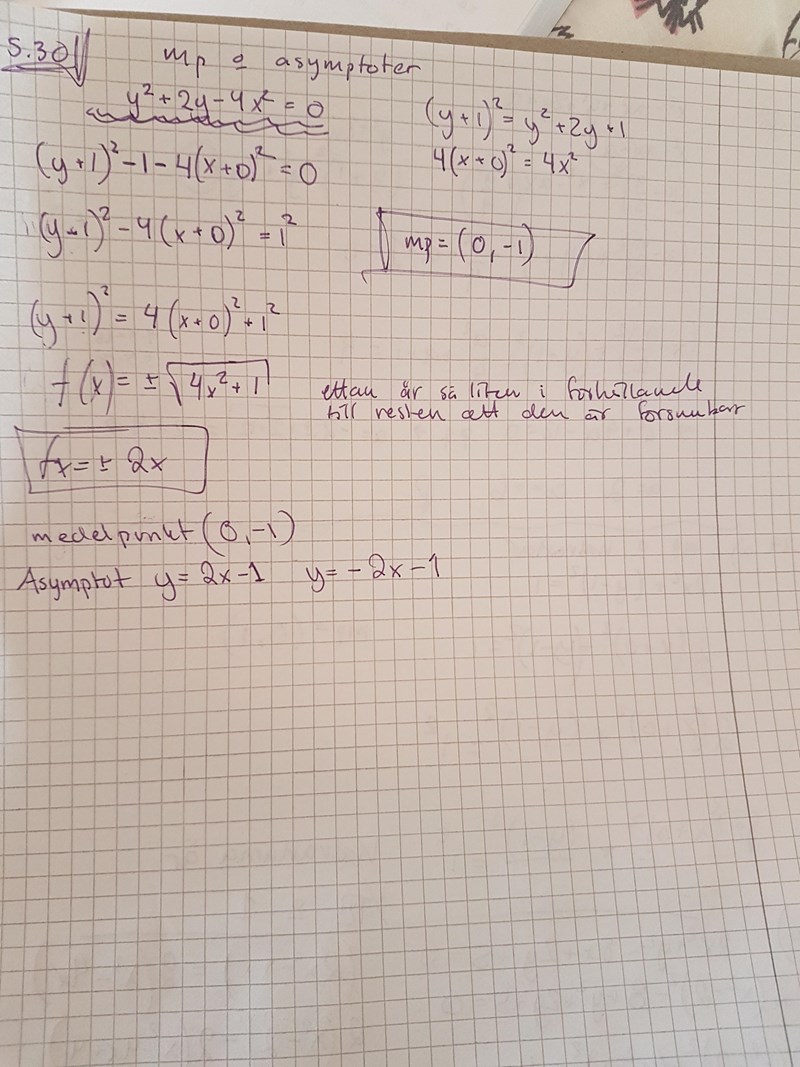
Standardfråga 1a: Har du ritat?

Smaragdalena skrev:

Standardfråga 1a: Har du ritat?

 Fast de jag undrar över är generellt inte specifikt för detta fall, fallet får bara statuera exempel. Och i detta fall är det ganska enkelt att se att det är rätt eftersom Mp ger x=0 så kommer y värdet också vara m-värde för båda asymptoterna. Men om x=a och a<0 eller a>0 så kommer inte de gälla. Men nu slog de mig att de borde ju bara vara att sätta in Mps värde tillsammans med den lutning jag redan fått fram i y=kx+m och lösa ut m... 

Ja, du har rätt, men du skulle kunna formalisera resonemanget när du tar fram själva asymptoten.

Det är ju så att en linjär asymptot $kx+m$ till en funktion $f(x)$ uppfyller:

$\lim_{x\to\infty}f\left(x\right)-\left(kx+m\right)=0$

För att få fram $k$-värdet kan man undersöka gränsvärdet:

$k=\lim_{x\to\infty}\dfrac{f(x)}{x}=\lim_{x\to\infty}\dfrac{-1\pm\sqrt{4x^2+1}}{x}=\lim_{x\to\infty}\dfrac{\pm2x}{x}=\pm2$

När man sedan har $k$-värdet kan man få fram $m$-värdet genom:

$m=\lim_{x\to\infty}f\left(x\right)-kx=\lim_{x\to\infty}-1\pm\sqrt{4x^2+1}-\left(\pm2x\right)=\lim_{x\to\infty}-1\pm x(\sqrt{4+\dfrac{1}{x^2}}-2)=$

$=\lim_{x\to\infty}-1\pm x\left(\sqrt{4+0}-2\right)=-1$

Därför får du asymptoterna $x=\pm2x-1$ när $x\to\infty$. Det kan även vara bra att i alla fall nämna att du undersöker asymptoter mot $x\to-\infty$, även om de i detta fall blir samma.

AlvinB skrev:

Ja, du har rätt, men du skulle kunna formalisera resonemanget när du tar fram själva asymptoten.

Det är ju så att en linjär asymptot $kx+m$ till en funktion $f(x)$ uppfyller:

$\lim_{x\to\infty}f\left(x\right)-\left(kx+m\right)=0$

För att få fram $k$-värdet kan man undersöka gränsvärdet:

$k=\lim_{x\to\infty}\dfrac{f(x)}{x}=\lim_{x\to\infty}\dfrac{-1\pm\sqrt{4x^2+1}}{x}=\lim_{x\to\infty}\dfrac{\pm2x}{x}=\pm2$

När man sedan har $k$-värdet kan man få fram $m$-värdet genom:

$m=\lim_{x\to\infty}f\left(x\right)-kx=\lim_{x\to\infty}-1\pm\sqrt{4x^2+1}-\left(\pm2x\right)=\lim_{x\to\infty}-1\pm x(\sqrt{4+\dfrac{1}{x^2}}-2)=$

$=\lim_{x\to\infty}-1\pm x\left(\sqrt{4+0}-2\right)=-1$

Därför får du asymptoterna $x=\pm2x-1$ när $x\to\infty$. Det kan även vara bra att i alla fall nämna att du undersöker asymptoter mot $x\to-\infty$, även om de i detta fall blir samma.

 Tack för svaret det gjorde de än begripligare!!