Att motivera en differentialekvation

Hej! Har en uppgift om ränta som jag har löst delvis men skulle behöva lite hjälp för att slutföra den. Tacksam för all hjälp!

När $n \to \infty$ motsvara det kontinuerlig beräkning av ränta på ränta som kan beskrivas med en differentialekvation. k(t) är ett kapital vid tiden t och k(0) = K. Om $∆ t$ är längden av en given ränteperiod beräknat i år och räntesatsen är p, kommer kapitalet mellan t och $t + ∆ t$ förändras enligt differentialekvationen $k (t + ∆ t) = k (t) (1 + p ∆ t)$ .

Uppgift

Motivera formeln och visa även att om $∆ t \to 0$ erhålls differentialekvationen $k' (t) = p k (t)$ .

Jag har gjort bevisdelen enligt följande steg

$k (t + ∆ t) = k (t) (1 + p ∆ t)$

$\Rightarrow$ $k (t + ∆ t) = k (t) + p ∆ t \cdot k (t)$

$\Rightarrow$ $k (t + ∆ t) - k (t) = p ∆ t \cdot k (t)$

Detta kan omskrivas till följande:

$\Rightarrow$ $\frac{k (t + ∆ t) - k (t)}{∆ t} = p k (t)$

När $∆ t \to 0$ blir svaret att VL är derivatans definition för k(t) och då får man diff.ekv $k' (t) = p k (t)$ , vilket skulle visas.

Min fråga till er är,

1.Stämmer mina uträkningar?

2. Hur kan jag på ett bättre vis motivera sista steget av min uträkning?

3. Hur kan jag motivera formeln $k (t + ∆ t) = k (t) (1 + p ∆ t)$ ?

Tacksam för all hjälp jag kan få!

1. Ja.

2. Det är som du säger, derivatans definition du får och använder, så det är OK.

3. Formeln säger att kapitalet k efter ett tidsintervall är lika med det ursprungliga kapitalet plus räntan. Denna beräknas som räntesatsen x kapitalet x tidsintervallet ifråga. Alltså 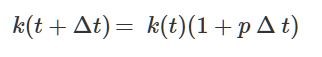vilket är det vanliga sättet att beräkna ränta, men vanligtvis är Δt ett år - här blir det mycket kortare.

HT-Borås skrev :
1. Ja.
2. Det är som du säger, derivatans definition du får och använder, så det är OK.
3. Formeln säger att kapitalet k efter ett tidsintervall är lika med det ursprungliga kapitalet plus räntan. Denna beräknas som räntesatsen x kapitalet x tidsintervallet ifråga. Alltså vilket är det vanliga sättet att beräkna ränta, men vanligtvis är Δt ett år - här blir det mycket kortare.

Okej, nu förstår jag! Tusen tack för din hjälp! Har du något förslag på hur jag skulle kunna motivera det sista steget av mitt bevis? Skulle vilja uttrycka det lite bättre men får inte till det.

Som ett annat skrivsätt kan du skriva:

$\lim_{∆ t \to 0} \frac{k (t + ∆ t) - k (t)}{∆ t} = k' (t) = p k (t) .$

Lirim.K skrev :
Som ett annat skrivsätt kan du skriva:
$\lim_{∆ t \to 0} \frac{k (t + ∆ t) - k (t)}{∆ t} = k' (t) = p k (t) .$

Smart, tusen tack! Har du något förslag på hur jag kan utveckla min motivering kring varför svaret blir just differentialekvationen k'(t) = pk(t)? Tacksam för svar :)

Hur kan du förklara den i ord? Om $k (t)$ är ett kapital vid tiden $t$ så är $k' (t)$ förändrignen av kapitalet vid tiden $t$ . Men du vet ju också att förändringen av kapitalet vid tiden $t$ är räntesatsen gånger kapitalet vid tiden $t$ , alltså $k' (t) = p k (t) .$

Hej!

Jag sitter idag i samma sits som dig och det vore mer än schysst ifall jag kunde få ta del av dina beräkningarna. Jag har själv spenderat en del tid med att försöka lösa uppgiften och jag tycker att det skulle vara väldigt givande samt lärorikt ifall jag fick möjligheten att jämföra mina tankar kring uppgiften med dina. Snälla, ifall du skulle kunna erbjuda mig möjligheten så kontakta mig via mitt Facebook konto: Emanuel Saliba. Jag väntar på svar och tack så mycket på förhand!!

Tog bort ett olämpligt inlägg. /moderator

Svara

Visa senaste svar