Avbildning R^2->R^2

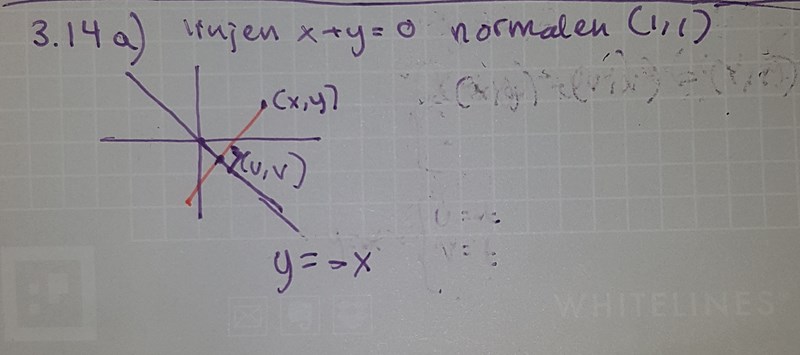
Som jag fattar det ska jag uttrycka (x,y) i (u,v), men jag vet inte hur jag ska göra det. Jag vet att denna har varit uppe på pluggakuten tidigare och även på andra ställen, men jag fattar ändå inte riktigt hur jag ska göra.
Vilken är ekvationen för den röda linjen?
Smaragdalena skrev:Vilken är ekvationen för den röda linjen?
Y=x+m?
Vilken är ekvationen för en rät linje som går genom punkterna (x,y) och (u,v) där vi dessutom vet att v=-u?
Om du har läst linjär algebra kan du använda att en riktningsvektor utmed linjen är
Bilda projektionen
Asså jag fattar nog inte alls vad det är jag ska göra eller hur jag ska komma dit 🤷♀️ upplever det som jag famlar i blindo
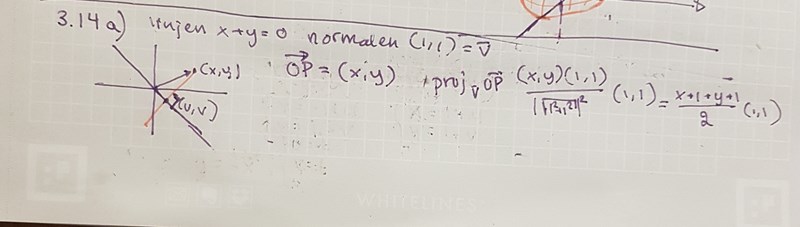
Smaragdalena skrev:Vilken är ekvationen för en rät linje som går genom punkterna (x,y) och (u,v) där vi dessutom vet att v=-u?
Det har låst sig helt i skallen. Jag fattar ibte vad det är jag ska göra tyvärr, just nu upplever jag det bara som obegripligt, trots att jag både läst i boken och kollat på föreläsningar.
Du vill alltså göra en vinkelrät projektion på linjen x+y=0, d v s linjen y=-x. Du behöver alltså hitta en linje som
- är vinkelrät mot linjen y=-x
- går genom punkten som du vill projicera, kalla den t ex (a,b)
Vilken riktningskoefficient har denna linje?
Om du tänker avbildning på x eller y axeln först så löser det sig!
(Vilket bra val av lärobok!)
Smaragdalena skrev:Du vill alltså göra en vinkelrät projektion på linjen x+y=0, d v s linjen y=-x. Du behöver alltså hitta en linje som
- är vinkelrät mot linjen y=-x
- går genom punkten som du vill projicera, kalla den t ex (a,b)
Vilken riktningskoefficient har denna linje?
1. y=x
2. Kallade jag (u,v)
k=(x-u)/(y-v) ?
Qetsiyah skrev:Om du tänker avbildning på x eller y axeln först så löser det sig!
(Vilket bra val av lärobok!)
Ska fundera lite på det när mitt barn sover 😊
Nu har du projicerat på linjens normal, det kan man använda, även om det blir lite mer omständligt.
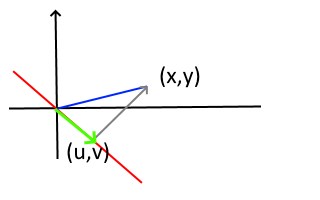
Du har räknat ut den grå pilen i bilden.
Du vill räkna ut den gröna pilen i bilden.
Den blå pilen är den gröna pilen + den grå pilen.
Om du subtraherar den grå pilen från den blå pilen får du den gröna pilen.
Alltså ska du bilda
Din projektion på normalen är nästan rätt, men det ska vara gånger, inte plus
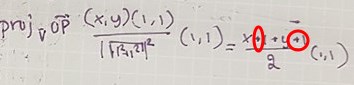
Jroth skrev:Nu har du projicerat på linjens normal, det kan man använda, även om det blir lite mer omständligt.
Du har räknat ut den grå pilen i bilden.
Du vill räkna ut den gröna pilen i bilden.
Den blå pilen är den gröna pilen + den grå pilen.
Om du subtraherar den grå pilen från den blå pilen får du den gröna pilen.
Alltså ska du bilda
Din projektion på normalen är nästan rätt, men det ska vara gånger, inte plus
Åhh tack för att du tog dig tid att illustrera! Verligen guld värt ❤. Oj ja där har jag gjort fel!

Tror jag äntligen börjar fatta! Är det någon som har lust att förklara det andra sättet att lösa det på också (nyfiken)?




