Avgör om den generaliserade integralen är konvergent
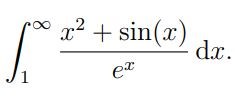
Hur ska göra, har fösökt lite men kom inte fram till något vettigt.
Termen sin(x) kan man kasta bort, för den är mindre än eller lika med 1, och täljaren är alltså mindre än eller lika med x2+1, och det är mindre än eller lika med 2x2. Så den intressanta integranden är x2e-x.
Laguna skrev:Termen sin(x) kan man kasta bort, för den är mindre än eller lika med 1, och täljaren är alltså mindre än eller lika med x2+1, och det är mindre än eller lika med 2x2. Så den intressanta integranden är x2e-x.
jaha... ska jag sedan använda partiel integration för att lösa den?
Har räknat får den till
om jag sätter in intervallet så får jag svaret, stämmer det?
Den primitiva funktionen ser inte rätt ut. Vad får du om du deriverar den?
Laguna skrev:Den primitiva funktionen ser inte rätt ut. Vad får du om du deriverar den?
oj har missat några minus tecken och ett e.
Den förhoppningsvis rätta versionen
BabySoda skrev:Laguna skrev:Den primitiva funktionen ser inte rätt ut. Vad får du om du deriverar den?
oj har missat några minus tecken och ett e.
Den förhoppningsvis rätta versionen
har deriverat den och fått x^2-e^-x, så den primitivaa funktionen stämmer.
Nu om jag sätter in intervallet så får jag svaret alltså funktionen är divergent.
Kan någon stämma av att jag har gjort rätt
Jag tycker din primitiva funktion borde gå mot noll.
Laguna skrev:Jag tycker din primitiva funktion borde gå mot noll.
ja det stämmer
så när x -> 1 så blir det
Men jag tror att jag har gjort ett fel för att om jag stoppar in
Varifrån kommer upgiften? Generaliserade integraler brukar inte ingå i Ma5. /moderator
Smaragdalena skrev:Varifrån kommer upgiften? Generaliserade integraler brukar inte ingå i Ma5. /moderator
Ja, det ska stå universitet, hade tryckt fel och försökt ändra men det gick inte
Det går endast att redigera sin tråd i två timmar efter att tråden postats. Tråden är nu flyttad till Matematik > Universitet. /moderator
vilket innebär att:
tomast80 skrev:vilket innebär att:
hänger inte med vad du gjorde där
tomast80 skrev:
förstår inte fortfarande, har jag kommit till rätt svar?
Det är enklare att inse att x^2/e^x < 1/e^0.5x för tillräckligt stora x. Denna funktionen är lätt att integrera.
parveln skrev:Det är enklare att inse att x^2/e^x < 1/e^0.5x för tillräckligt stora x. Denna funktionen är lätt att integrera.
ja men är det sättet jag löste uppgiften med, fel?
Du skrev bara , om jag inte har missat nåt. Det räcker inte.
Laguna skrev:Du skrev bara , om jag inte har missat nåt. Det räcker int
menar du att jag ska skriva så här
men nu när jag tänker på det blir eller är det odefinierad?
funktionen blir konvergent, det har ett ändligt värde







