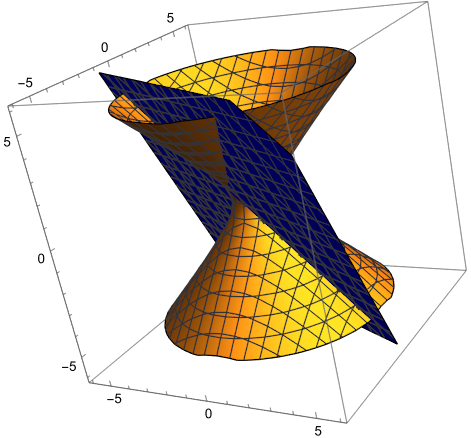
Avgör om planet är ett tangentplan till ytan

Ett tangentplan till en yta är ett plan som tangerar ytan.

Laguna skrev:

Ett tangentplan till en yta är ett plan som tangerar ytan.

Ja precis och det gör den i en specifik punkt.  

Så är det.

Laguna skrev:

Så är det.

Men hur hittar man den punkten? 

Jag skulle ta reda på om normalvektorn till planet är en normalvektor till ytan någonstans.

Laguna skrev:

Jag skulle ta reda på om normalvektorn till planet är en normalvektor till ytan någonstans.

Du menar om normalvektor till planet är parallell med normalvektor till ytan ?  Men om man deriveriverar ytan så får man ju gradienten till f.

Ja, du kan tänka dig att $f(x,y,z)=x^2+y^2-z^2$

Ytan i frågan är då nivåytan $f(x,y,z)=1$

Gradienten av en funktion är vinkelrät mot dess nivåytor.

D4NIEL skrev:

Ja, du kan tänka dig att $f(x,y,z)=x^2+y^2-z^2$

Ytan i frågan är då nivåytan $f(x,y,z)=1$

Gradienten av en funktion är vinkelrät mot dess nivåytor.

ja precis och om gradienten är vinkelrät mot dess nivåyta så kan man ju ta godtycklig punkt tex (1,0,0) som ligger i ytan. då blir gradienten i den punkten (2,0,0). Problemet är att den punkten inte statisfierar planets ekvation. Men tex punkten (0,-1,0) statisfierar både ytan och planet.

I en eventuell tangeringspunkt är planets normal och ytans normal parallella. Du letar alltså efter punkter sådana att

$\nabla f =\lambda (1,2,1)$, för något $\lambda\in\mathbb{R}$.

När du hittat alla sådana möjliga punkter är det bara att se om någon av dem uppfyller såväl planets- som ytans ekvation.

D4NIEL skrev:

I en eventuell tangeringspunkt är planets normal och ytans normal parallella. Du letar alltså efter punkter sådana att

$\nabla f =\lambda (1,2,1)$, för något $\lambda\in\mathbb{R}$.

När du hittat alla sådana möjliga punkter är det bara att se om någon av dem uppfyller såväl planets- som ytans ekvation.

Jag vet inte om mitt sätt är att föredra. Men jag hittade tangentplanet till ytan i den gemensamma punkten (0,-1,0) för ytan  samt för planet. Deras normalvektorer verkar inte vara parallella enligt min lösning. Jag kanske ska undvika att lösa den på det sättet då det här gäller bara för en punkt och inte för alla andra som kan potentiellt stämma 

Ytan och planet har många gemensamma punkter. Men det är faktiskt bara i en punkt som de sammanfaller och som ytans normal har samma riktning som planets normal. Tänk på att planets normal är (1,2,1). I tangeringspunkten måste normalen till ytan vara parallell med den vektorn.

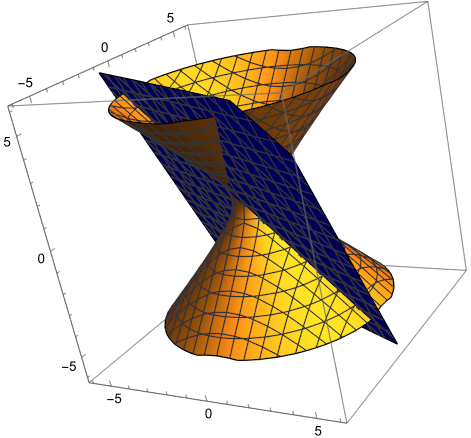
D4NIEL skrev:

Ytan och planet har många gemensamma punkter. Men det är faktiskt bara i en punkt som de sammanfaller och som ytans normal har samma riktning som planets normal. Tänk på att planets normal är (1,2,1). I tangeringspunkten måste normalen till ytan vara parallell med den vektorn.

Yes då förstår jag. Så jag ska börja med hitta först gradienten till ytan och sen hitta de potentiella punkter som normalen till planet och gradienten till f träffar varandra och leder till att ytans normalvektor i dessa punkter är parallell med planets normalvektor?