Avgöra om en serie med cosinus är konvergent

Hej,

Här är ju $k$ ett positivt heltal, varför serien är $\cos\left(\pi\right)+\cos\left(2\pi\right)+\cos\left(3\pi\right)+\cos\left(4\pi\right)+\cos\left(5\pi\right)+...$ Kom ihåg att cosinus är en $2\pi$ periodisk funktion.

Men cos kpi = 1 om k är jämnt och -1 om k är udda. Följden av delsummor har två delföljder, den ena konstant =0 och den andra divergerar mot - oändl.. Serien är därför divergent. 

Serien hoppar mellan $-1$ och $0$.

MN_BD skrev:

Jag ska undersöka om serien $\sum _{k=1}^{\infty }\cos \left(k\pi \right)$ är konvergent. Jag försökte avgöra om $\underset{k\to \infty }{\lim }\cos \left(k\pi \right)$ är nollskilt men jag förstår inte hur gränsvärdet ska lösas. Finns det något sätt att resonera fram om den är konvergent eller divergent?

Det du är inne på här funkar också. Om serien skall vara konvergent så måste gränsvärdet av termerna gå mot noll (i alla fall gränsvärdet över heltalen).

$\lim_{k\to\infty}\cos\left(k\pi\right)=\lim_{k\to\infty} \left(-1\right)^k$ existerar inte, alltså kan serien inte heller konvergera.

En brasklapp att lägga in här är dock just det här med att det rör sig om ett gränsvärde över heltalen. Tar vi till exempel

$\displaystyle\sum_{k=1}^\infty \sin\left(\dfrac{k^2+1}{k}\pi\right)$

kan man lätt luras att tro att gränsvärdet

$\lim_{k\to\infty}\sin\left(\dfrac{k^2+1}{k}\pi\right)$

inte existerar och att serien är divergent. Och mycket riktigt existerar inte gränsvärdet om vi skulle titta på reella tal $k$, men faktum är att över heltal $k$ existerar gränsvärdet:

$\sin\left(\dfrac{k^2+1}{k}\pi\right)=\sin\left(\pi k+\dfrac{\pi}{k}\right)=\cos\left(\pi k\right)\sin\left(\dfrac{\pi}{k}\right)=\left(-1\right)^k\sin\left(\dfrac{\pi}{k}\right)\to0$ när $k\to\infty$.

Det går också att med Leibniz kriterium visa att serien faktiskt är konvergent (som bekant är ju ett sådant här gränsvärde nödvändigt, men inte tillräckligt för att serien skall konvergera!).

Också lite kul tröst om sånt här känns svårt ibland är att inte ens Wolfram Alpha alltid vet vad den håller på med:

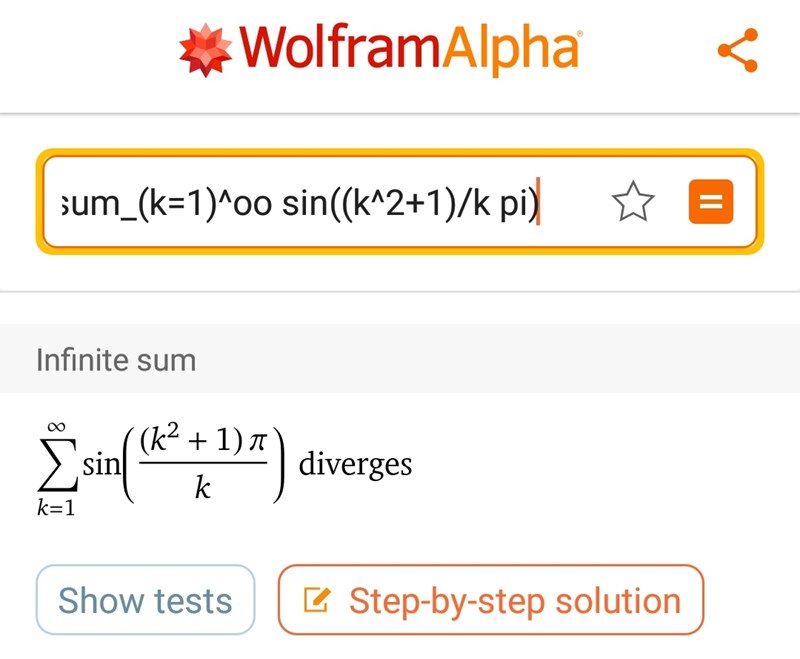
(Det här är fel; serien konvergerar)