Avstånd mellan två städer. (Fysik/Fysik 1)

Det här är min tankegång

Känns svaret rimligt? 58 m avstånd mellan två städer.

Jag föreslår att du använder ett visuellt/grafiskt resonemang.

Rita två vt-grafer: En där hastigheten är konstant 70 km/h och en där hastigheten på första delen är 60 km/h och den andra är 80 km/h.

Du vet att arean under de båda graferna är lika stor (avståndet mellan de båda städerna).

Du vet vidare att arean under 60 km/h-grafen är lika stor som arean under 80 km/h-grafen.

Slutligen vet du att den "lagliga" grafens utsträckning är 3 minuter (dvs 0,05 timmar) längre än den "olagliga" grafen.

Kommer du vidare då?

PATENTERAMERA skrev:
Känns svaret rimligt? 58 m avstånd mellan två städer.

Du har rätt.

Yngve skrev:
Jag föreslår att du använder ett visuellt/grafiskt resonemang.

Rita två vt-grafer: En där hastigheten är konstant 70 km/h och en där hastigheten på första delen är 60 km/h och den andra är 80 km/h.

Du vet att arean under de båda graferna är lika stor (avståndet mellan de båda städerna).

Du vet vidare att arean under 60 km/h-grafen är lika stor som arean under 80 km/h-grafen.

Slutligen vet du att den "lagliga" grafens utsträckning är 3 minuter (dvs 0,05 timmar) längre än den "olagliga" grafen.

Kommer du vidare då?

Jag brfukar undvika rita vt-grafer eftersom det känns mer naturligt att rita som jag gör med bild eftersom det hjälper föreställa fenomenet med bild och text.

Ja, du kan rita en bild av en bil och två städer, det är en utmärkt början.

vt-graferna var bara tänkta att hjälpa dig att ställa upp de relevant ekvationerna.

Men det går bra att göra det även utan det stödet.

Om vi skippar det första steget så kan du gå direkt på ekvationerna.

Inför de obekanta storheterna:

x som avser avståndet (i kilometer) mellan de två städerna.
t1 som avser tiden (i timmar) det tar att köra lagligt.
t2 som avser tiden (i timmar) det tar att köra olagligt.

Använd nu sambandet s = v*t för att ställa upp ekvationer för det du vet.

Tips 1: Om Peter kör lagligt så kär han 60 km/h i x/2 km och 80 km/h i x/2 km.

Tips 2: 3 minuter = 0,05 timmar.

jag gör ett försk med vt-grafer. Men, jag undrar hur jag kunde förbättra min bild eller hur du skulle ritat det som jag föreställde mig ?

Din bIld är bra, men den ger inte så mycket hjälp i att ställa upp ekvationerna.

Vad gäller din uträkning så vore det intressant att veta hur du tänker när du beräknar en medelacceleration och använder den plus starthastigheten tillsammans med tiden 3 minuter i formeln för position s(t)?

Tillägg: 6 aug 2025 08:09

Du blandar även enheter i din uträkning av medelhastighet (meter per sekund i täljaren och minuter i nämnaren).

Yngve skrev:
Ja, du kan rita en bild av en bil och två städer, det är en utmärkt början.

vt-graferna var bara tänkta att hjälpa dig att ställa upp de relevant ekvationerna.

Men det går bra att göra det även utan det stödet.

Om vi skippar det första steget så kan du gå direkt på ekvationerna.

Inför de obekanta storheterna:

x som avser avståndet (i kilometer) mellan de två städerna.

t1 som avser tiden (i timmar) det tar att köra lagligt.

t2 som avser tiden (i timmar) det tar att köra olagligt.

Använd nu sambandet s = v*t för att ställa upp ekvationer för det du vet.

Tips 1: Om Peter kör lagligt så kär han 60 km/h i x/2 km och 80 km/h i x/2 km.

Tips 2: 3 minuter = 0,05 timmar.

Jag vet inte hur jag ska ställa upp ekvatgionerna på ett bra sätt ?

Så här tänker jag

(^ー^)

Börja med att köra olagligt.

Använd s = v*t för att ställa upp sambandet mellan sträckan x, hastigheten 70 km/h och tiden t2.

Blir då ett ekvationssystem mellan

tiderna olagligt och lagligt ?

Ja, så kan det bli.

Ta ett steg I taget. Börja med att ta fram ett samband mellan x, 70 km/h och t2.

Yngve skrev:
Ja, så kan det bli.

Ta ett steg I taget. Börja med att ta fram ett samband mellan x, 70 km/h och t2.

ska det bli så här :

$s = v t s = x x = 70 t_{1} x = 80 (t + 0.05)$

Nej, det stämmer iinte.

Rad tre är nästan rätt, men du blandar ihop t1 och t2.

Den "olagliga" hastigheten är 70 km/h och den "olagliga" tiden är t2.

Det borde ge dig x = 70*t2, eller hur?

Jag har svårt att förstå vilka jag ska utgå ifrån eftersom jag tre hastigheter enligt texten.

70, 60 och 80 km/h

Vilka är de relevanta i mitt ekvationssystem ?

Yngve skrev:
Nej, det stämmer iinte.

Rad tre är nästan rätt, men du blandar ihop t1 och t2.

Den "olagliga" hastigheten är 70 km/h och den "olagliga" tiden är t2.

Det borde ge dig x = 70*t2, eller hur?

Men vad blir då x ?

Hur tar jag mig vidare därifrån ?

Arup skrev:
Jag har svårt att förstå vilka jag ska utgå ifrån eftersom jag tre hastigheter enligt texten.

70, 60 och 80 km/h

Vilka är de relevanta i mitt ekvationssystem ?

I texten står det att det är två olika resor.

En resa avser x km, sker med den konstanta hastigheten 70 km/h och den tar t2 timmar.

Det ger dig en ekvation x = 70*t2.

Den andra resan avser x/2 km i 60 km/h, sedan x/2 km i 80 km/h och den resan tar totalt t1 timmar.

Går det att hålla isär resorna och de obekanta storheterna då?

Skulle du kunna ställa upp ekv systemet ?

Så löser jag den

Nja, jag tror att det du behöver träna på är just att ställa upp ekvationerna. Att lösa dem tror jag att du redan kan.

Tänk så här: Eftersom s = v*t så är t = s/v.

Du vet att den andra resan har hastigheten 60 km/h under x/2 km och 80 km/h under x/2 km.

Du vet att dessa delar tillsammans tar t1 timmar.

Försök nu att ställa upp en ekvation för detta, dvs t1 = (någonting med x/2, 60 km/h och 80 km/h).

Ska jag addera de två?

Arup skrev:
Ska jag addera de två?

Ja, den sammanlagda tiden (dvs t1) är summan av tiden för de båda delsträckorna.

Jag gör et nytt försök imorgn.

Ett försök även om fysik inte är min "forte". Kanske det finns kortare lösning.

Visa spoiler

Nu har Trinity 2 lösa den. Men var det så här du menade Yngve ?

Arup skrev:
Nu har Trinity 2 lösa den. Men var det så här du menade Yngve ?

Nix. Jag tror mig veta vad Yngve vill att du gör. Du kan lugnt arbeta vidare från #22. (Ofta finns det fler vägar till lösningen.)

Arup skrev:
Nu har Trinity 2 lösa den. Men var det så här du menade Yngve ?

Ja, det var det jag menade i svar #4.

Men eftersom du inte ville använda vt-grafer som hjälp att formulera ekvationerna så påbörjade jag en annan väg.

Hoppas du ändå ser att grafer kan underlätta förståelsen.

Yngve är offline, så jag tar det vidare en bit.

Den här har du koll på, sambandet mellan sträcka, hastighet och tid: $s = v t \leftrightarrow t = \frac{s}{v}$

Vi bestämmer också att t₁ är tiden för laglig körning, samt att t₂ är tid för olaglig.

Vet vet även att det tar 3 minuter längre tid att köra lagligt: $t_{1} = t_{2} + 0, 05 1$

Att olagligt köra hela sträckan s i 70 km/h tar förstås: $t_{2} = \frac{s}{70} 2$

Nu har vi tre obekanta (t₁, t₂ och s), men bara två ekvationer. Vi behöver ytterligare en för att kunna lösa!

Hur lång tid tar det då att lagligt köra halva sträckan s i 60 km/h och sedan halva sträckan s i 80 km/h?

Jo: $t_{1} = . . . 3$

(Nu ser jag att Yngve är online, så jag pausar. Det var där ni slutade igår kväll.)

hur tar jag mig vidare därifrån och bildar ett fullständigt ekv. system ?

Arup skrev:
hur tar jag mig vidare därifrån och bildar ett fullständigt ekv. system ?

Läs vad Yngve skriver i #22 och fundera lite.

Arup skrev:
hur tar jag mig vidare därifrån och bildar ett fullständigt ekv. system ?

Jag föreslår att du fortsätter tankegången vi var inne på igår, dvs från svar #24

jag gör ett tull försök

Ja, gör det.

Tips:

Tiden det tar att köra första halvan av sträckan lagligt får du med hjälp av t = s/v, där s = x/2 och v = 60 km/h.
Tiden det tar att köra andra halvan av sträckan lagligt får du med hjälp av t = s/v, där s = x/2 och v = 80 km/h.
Den totala tiden det tar att köra hela sträckan lagligt, dvs t1, är summan av dessa två tider

Asså jag får $t_{1} = \frac{s + 3, 5}{70}$

Visa hur du kommer fram till det.

jag adderade de två som sictransi menade i #30

Yngve är det så här du menar ?

Arup skrev:
Yngve är det så här du menar ?

Ja, om vi undviker att avrunda i det här läget så får vi mycket riktigt t1 = 2,8x/192.

Du vet redan ett samband mellan t2 och x.

Då har du tre obekanta storheter t1, t2 och x, men bara två ekvationer.

Som tur är kan vi ta fram en tredje ekvation med hjälp av ett givet samband mellan t1 och t2.

Försök att formulera det som en ekvation och skriv sedan alla tre ekvationer tydligt.

är det den som kör 70 km/h ?

jag vet inte vilket samband du menar som jag kan får fram mellan t1 och t2

Arup skrev:
är det den som kör 70 km/h ?

Menar du var du hittar sambandet mellan x och t2? I sp fall är svaret ja. Annars vet jag inte vad du menar.

Arup skrev:
jag vet inte vilket samband du menar som jag kan får fram mellan t1 och t2

Läs uppgiften noga igen, dör står det hur t1 och t2 förhåller sig till varandra.

Jag pekar Inte ut det i texten ännu, för jag vill att du ska öva på just detta, att läsa uppgiftstexten och översätta det till "mattespråket".

det står ju om han håller 70 km/h så kommer det ta min längre

3 min

Ja. Du vet alltså att det skiljer 3 minuter mellan t1 och t2. Det ger dig ett samband mellan dessa två storheter. Här kan det vara lätt att göra fel, så tänk efter innan du ställer upp den ekvationen. Visa oss sedaan den innan du räknar vidare.

Tips: 3 minuter = 0,05 timmar

jag tänker så här:

$\{\begin{cases} T_{t o t} = 0, 146 x \\ x = 0.05 \times 70 \end{cases}$

OK, det betyder alltså att x = 3,5 km (vilket inte stämmer) och att T_tot = 0,511.

Men vad betyder T_tot?

summan av t1 och t2

Arup skrev:
summan av t1 och t2

Varför ska du summera t1 och t2? Det är inte det som efterfrågas.

Läs uppgiften noga igen. Vad är det som efterfrågas?

Och vilken av våra obekanta storheter betecknar det?

=====

Vad är det alltså vi ska bestämma? Är det t1, t2, x eller något helt annat?

Jag föreslår att du istället fortsätter tankegången vi var inne på, dvs från svar #48

Och att du följer det spåret enligt de tips du får, ett steg i taget.

Är det så här ni menar ?

Bra!

Allt stämmer (förutom att du har råkat skriva 3360 istället för 33600 på två ställen).

Kolla nu lösningen som Trinity2 gav i svar #26.

Hängde du med på den?

Yngve skrev:
Bra!

Allt stämmer (förutom att du har råkat skriva 3360 istället för 33600 på två ställen).

Kolla nu lösningen som Trinity2 gav i svar #26.

Hängde du med på den?

Jag tycker Trinity 2:s lösning var svårare att förstå eftersom jag mer bekant med att ställa upp ekv systemet som du förespråkade om dvs s=vt

halva sträckan i det här fallet x =x/2 och sen löser vi tiderna utifrån hastigheterna.

Tjusigt!

Som en extra bonus kan vi fundera på hur tidsangivelsen "3 minuter" slår på redovisningen av resultatet.

168 km har tre gällande siffror, medan "3 minuter" bara har en.

Justerar vi tiden +/- 30 sekunder (fortfarande "3 minuter" avrundat) så slår det +/- 15 km ungefär på avståndet.

Borde vi svara med 170 km, eller kanske enbart en enda värdesiffra, 2*10² km?

Jag spekulerar bara, uppgiften är löst, men en lärare kanske skulle tycka frågan var relevant.

Själv har jag inget riktigt 100%-igt svar.

Vore jag tvungen att välja skulle jag skriva 168 km ≈ 2*10² km.

Arup skrev:

Jag tycker Trinity 2:s lösning var svårare att förstå eftersom jag mer bekant med att ställa upp ekv systemet som du förespråkade om dvs s=vt

halva sträckan i det här fallet x =x/2 och sen löser vi tiderna utifrån hastigheterna.

Trinity2 använder också sambandet s = v*t i sin lösning.

Du behöver inte göra exakt på samma sätt, men fundera på om inte just bilden skulle hjälpa dig att sätta upp just de ekvationer som du använde i din lösning.

Jag tror att om du vänjer dig vid att illustrera problemen på liknande sätt så kommer det att bli betydligt enklare för dig att ställa upp relevanta ekvationer.

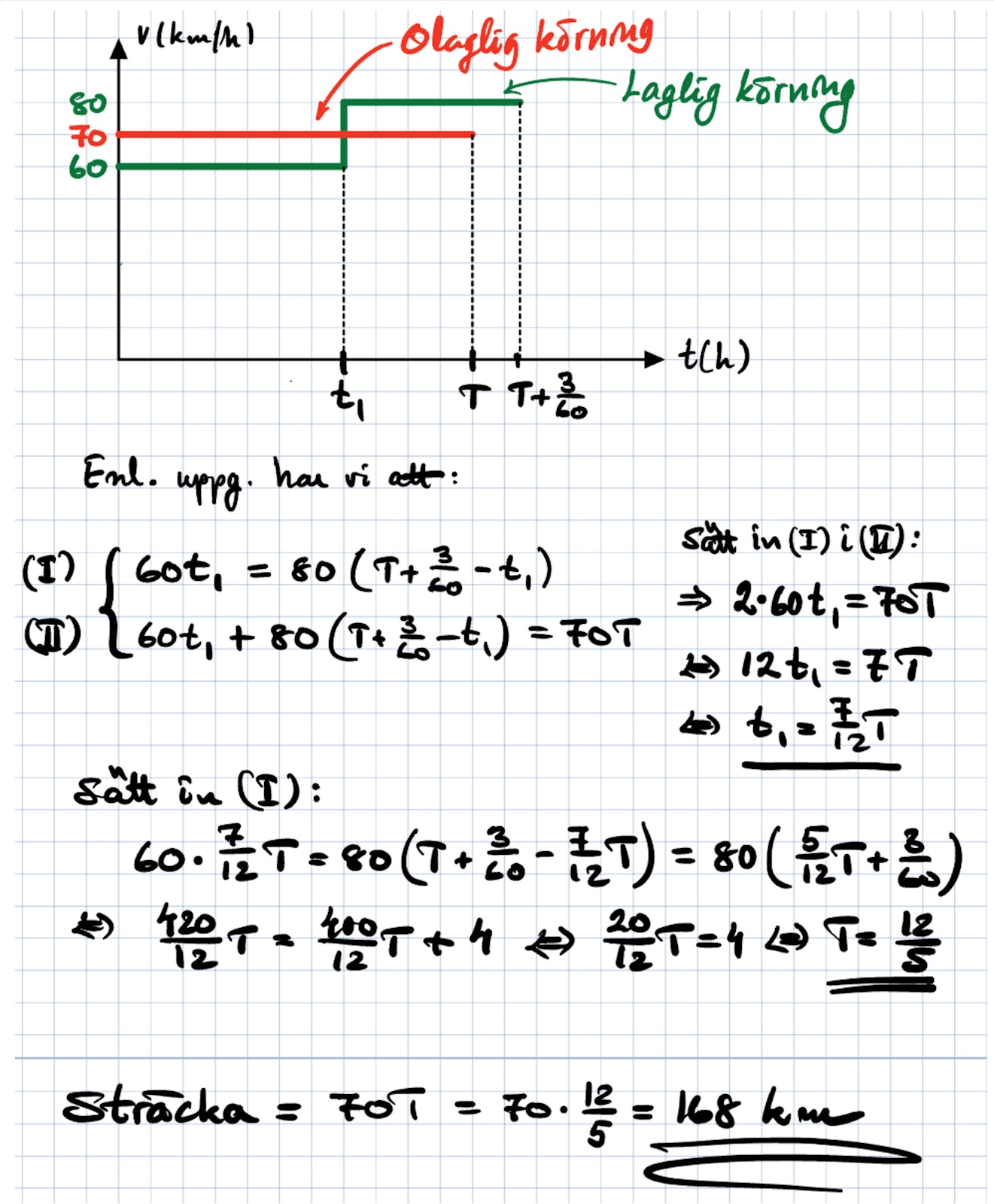
Bilden säger precis de saker vi har använt till din lösning:

Den lagliga körningen (grön): Först halva sträckan i 60 km/h, sedan resterande halva i 80 km/h. Arean under båda dessa är lika stor.

Den olagliga körningen (röd): Hela sträckan i 70 km/h. Arean under denna graf är lika stor som den sammanlagda Arean under den gröna grafen.

Skillnaden i tid är 3/60 timmar.

Hur illustrerar bilden att den olagliga hastigheten dvs 70 km/h är lika som den sammanlagda Arean under den gröna grafen ? Hur kjan se att arean för både 60 km/h och 80 km/h är lika stora ?

Att arean under den gröna grafen (dvs totalt tillryggalagd sträcka vid laglig körning) är lika stor som arean under den röda grafen (dvs totalt tillryggalagd ströcka vid olaglig körning) vet man, eftersom det är givet i uppgiften. Det är nämligen avståndet mellan de två städerna, och det ändras inte mellan körningarna.

Bilden används inte för att räkna rutor och mäta, utan istället som tankestöd för att ställa upp ekvationer för de samband som finns.

Därför behöver bilden inte vara skalenligt ritad.